航空液压油泵车保障能力建模仿真
李 康, 黄之杰, 吴潇洁
(空军勤务学院航空四站系, 江苏 徐州 221000)
航空液压油泵车用于在飞机发动机停机状态下,以一定的压力、流量和符合污染度等级要求的工作介质,为飞机液压系统提供检修动力,或为飞机补充加注液压油及净化飞机液压系统[1]。随着现代战机功能和结构的复杂化,对航空液压油泵车的保障需求愈加突出。当前,针对航空液压油泵车保障能力评价问题的研究相对较少,因此,缺乏评价各型航空液压油泵车实际保障能力的有效方法。笔者从任务角度出发,综合考虑航空液压油泵车的系统结构、维修活动和保障任务等因素,探讨航空液压油泵车保障能力评价问题。
1 评价参数
保障能力是指在既定的使用环境和任务要求条件下,装备执行规定任务所能达到预期效果的能力,是装备的固有属性[2]。从装备保障性角度考虑,保障能力主要是指装备的设计特性及预设资源能够满足使用要求的能力[3]。由于装备类型、系统结构、任务范围、保障资源和使用环境的不同,描述不同装备保障能力的评价参数也不相同,不存在统一适用的评价参数,比较常用的参数有使用可用度、任务成功率、备件短缺风险、备件利用率和平均修复时间等[4]。航空液压油泵车的主要任务是为飞机提供液压动力或更换补充油液,所关注的重点是当有保障需求时,装备能够执行任务的能力和任务完成情况等。因此,笔者选取使用可用度、任务成功率和备件短缺风险作为航空液压油泵车保障能力的评价参数。
使用可用度(AO,operational availability)是指装备服役后,在保障资源与使用环境既定的条件下,当有保障需求时装备能够投入使用的能力,是与装备能工作时间和不能工作时间有关的一种可用性度量参数[5]。
任务成功率(Pmcs,mission completion success probability)是指在外部条件既定的情况下,装备成功完成规定任务的概率,是装备维修性与可靠性的综合描述[6]。
备件短缺风险(ROS,risk of spare parts shortage)是指在特定条件下备件库存无法满足需求的概率,是检验库存对备件需求满足程度的重要指标。
2 仿真评价模型
根据航空液压油泵车的使用保障特点及评价要求,其保障能力评价模型应包括装备结构模型、任务模型、保障资源模型、维修活动模型和仿真计算模型。为简化所建模型,作如下基本假设:
1)航空液压油泵车各功能单元之间是串联关系,故障相互独立,只要某一个组成单元发生故障,即认为系统故障;
2)航空液压油泵车及其组成部件只有工作与故障2种状态,且单元更换后不影响装备的正常功能;
3)系统及组成单元的故障和维修活动独立进行,各单元的寿命和维修时间服从指数分布;
4)维修活动不单独考虑维修人员及其作业效率,也不单独考虑装备、设备的使用情况;
5)各级维修站点的维修能力以及备品备件的基本类型、部署地点及数量均已知。
2.1 装备结构模型
航空液压油泵车包含多个功能子系统,各子系统又由众多单元构成。在实际使用保障过程中,多是由于单元发生故障而进行装备维修,根据各单元是否可修、是否现场可修或需要返回车间修理,可将其分为如下6类:
1)现场可更换单元(Line Replaceable Unit,LRU),其在系统上可修或可直接更换;
2)站点可更换单元(Station Replaceable Unit,SRU),其在维修站点可修或可更换;
3)现场部分可修单元(Partial Repairable Unit,PRU),其在系统上部分可修或更换后具有一定的修复概率;
4)站点部分可修单元(Station Partial Repairable Unit,SPRU),其在维修站点部分可修或更换后具有一定的修复概率;
5)现场可报废单元(Discard Unit,DU),其在系统中不可修复;
6)站点报废单元(Discard Partial Unit,DP),是从可修单元上直接更换的不可修件。
图1为航空液压油泵车的系统结构。结合其各子系统和组成单元之间的串、并联关系,可定义完整的装备结构模型。其中:各单元的装机数量、故障率、维修时间、运行比和环境影响因子等为模型输入。

图1 航空液压油泵车系统结构
2.2 任务模型
任务是仿真活动的主要驱动[7],笔者首先采用组合分析法对航空液压油泵车的保障任务进行分解,对其基本任务进行分析和描述,然后依据任务剖面间的逻辑关系建立任务模型。
航空液压油泵车的保障任务主要包括提供检修液压源、补充加注液压油和净化飞机液压系统3大类。根据航空液压油泵车的任务执行过程,简化后的任务剖面模型如图2所示。
由于航空液压油泵车所执行的3类任务是相互独立的,因此,各任务剖面之间为并联关系,根据任务剖面和模型的假设条件,建立任务使用模型,如图3所示。

图2 航空液压油泵车的简化任务剖面模型

图3 航空液压油泵车任务使用模型
2.3 保障资源模型
影响航空液压油泵车保障能力的因素众多,其中备件资源、保障设备、保障设施和人力资源的影响最为突出。当航空液压油泵车发生故障或进行预防性维修时,若部分组成单元的可靠度无法满足继续使用条件,均会出现备件需求。设
H={L,M,P},
(1)
式中:L={Ll1,Ll2,…,Lll},为保障设备集合,l为保障设备种类数,Lli(i=1,2,…,l)为第i种保障设备的数量;M={Mm1,Mm2,…,Mmm},为保障设施集合,m为保障设施种类数,Mmj(j=1,2,…,m)为第j种保障设施的数量;P={Pp1,Pp2,…,Ppp},为维修人员集合,p为维修人员级别数量,Ppz(z=1,2,…,p)为某级维修站点第p种级别维修人员的数量。保障资源建模主要从维修站点的角度综合考虑各维修站点的保障设施、保障设备和维修人员配置情况,描述各维修站点的保障能力。
2.4 维修活动模型
维修活动分为预防性维修和修复性维修。预防性维修主要与任务时间、任务数量和日历时间参数有关[8]。可能出现的问题是在某一时间段内多个系统同时出现预防性维修请求,为避免这一情况的发生,仿真时预设限制条件,系统会根据最近一次任务请求和下一次预防性维修任务标志、时间等参数预先进行调整。
修复性维修主要包括对可修单元的修复作业和不可修单元的更换作业。若航空液压油泵车在执行任务中发生故障,则在外场对可更换故障单元进行拆卸,然后在维修站点间流动,直至被修复。更换的故障单元可通过库存备件、串件或修复故障单元获取,若由修复故障单元获得,需要根据故障单元的故障模式及复杂程度确定可修复的维修站点。航空液压油泵车各组成单元的故障发生时机和模式可通过蒙特卡罗方法随机抽样得到。

(2)
式中:d为维修站点数量;N为单元总数。
设Fk(x=r)为单元k在第r级维修站点的修复概率,则
(3)
x的分布函数为
(4)
式中:x=1,2,…r,为维修站点级别数量,Hk(x)为单元k在第r级维修站点的累计修复比,用来描述保障组织中各级站点的维修能力。为避免出现可修故障单元无法修复的问题,定义最高级维修站点的可修故障单元的累计修复比为1。
对于不可更换单元,可通过直接维修或更换下级故障单元进行修复,其维修逻辑关系如图4所示。若对故障单元进行原位维修或更换下级故障单元,则有时间和资源需求,多个单元同时出现维修需求则会导致资源竞争,因此,仿真时应设定在有限的保障资源中维修耗时最短的作业享有优先调用权。

图4 不可更换单元修复过程
2.5 仿真计算模型
2.5.1 使用可用度仿真计算模型
根据实际保障情况,航空液压油泵车不可工作时间主要由维修时间(Maintenance Time,MT)、保障延误时间(Logistic Delay Time,LDT)和管理延误时间(Managing Delay Time,ADT)组成,可工作时间由执行任务时间(Operation Time,OT)和待命准备时间(Stand-to Time,ST)组成,其服役后总日历时间(Total Time,TT)构成如图5所示。
由图5可以看出:从时间角度考虑,使用可用度

图5 航空液压油泵车服役后总日历时间构成
AO为
(5)
在不考虑非工作时间的情况下,可用总工作时间表示总任务时间,可工作时间表示装备能完成任务的时间。因此,从任务角度考虑,使用可用度AO为
(6)
2.5.2 任务成功率仿真计算模型
为使仿真结果更贴近装备使用保障的实际情况,需要多次重复仿真,但每次仿真都会触发不同的随机种子数且仿真结果也会有所差别。单次仿真时任务成功率表示固定任务在任务剖面中的成功情况,如果任务成功率达到仿真所设定的任务成功点,则该次任务被记录为成功任务,统计仿真周期内所有成功任务,该数值与仿真总任务次数的比值即为本次任务成功率[9],即
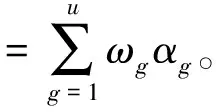
(7)
式中:
为固定任务在第g个任务剖面中的可靠度;
为第g个任务剖面占总任务剖面的比重;u为仿真周期内总任务次数。
在整个仿真周期内,航空液压油泵车任务成功率为所有任务剖面中成功完成的固定任务次数与总任务次数的比值,即
(8)
2.5.3 备件短缺风险仿真计算模型
备件短缺风险(ROS)和备件保障率(Psps,spare parts supply probability)是相对而言的,对于相同条件下的同一维修站点,其备件短缺风险和备件保障率之间存在如下关系:
ROS+Psps=1。
(9)
从单个组成单元的角度来看,备件保障率可采用航空液压油泵车的各组成单元备件保障率的代数期望值表示。如果航空液压油泵车在时间间隔T内,第k(1≤k≤N)个单元需要进行Nk(T)次更换作业,其实际库存数量为Mk(T),则第k个单元的备件保障率为
(10)
航空液压油泵车的备件总保障率为
(11)
若第k个单元在时间间隔T内出现故障的概率为λk,则备件总保障率为
(12)
由此可得备件短缺风险为
ROS=1-Psps。
(13)
2.5.4 蒙特卡罗统计实验及离散事件模型
设航空液压油泵车各子系统的可靠性与维修性
均为服从某一分布的随机变量,这里假设均服从指数分布,根据蒙特卡罗抽样原理,对收集的平均故障间隔时间(Mean Time Between Failure,MTBF)和平均修复时间(Mean Time To Restoration,MTTR),在[0,1]内抽取随机数δ,根据替换法和逆变法可得一次故障后各子系统的随机寿命Ts和故障修复时间Tm分别为
Ts=-MTBF×lnδ,
(14)
Tm=-MTTR×Inδ。
(15)
由于装备(系统)的状态是时间连续、状态离散的马尔科夫过程[10],因此在仿真时可建立子系统状态列表,根据相邻事件系统状态不变来确定仿真步长。
3 仿真原理与流程
运用蒙特卡罗理论与事件调度法,以基本任务为出发点,考虑资源优化配置及多级维修站点情况,模拟航空液压油泵车及功能单元的各种事件,如任务、故障、预防性维修、修复性维修,以及备件配置与调配等,仿真航空液压油泵车在给定条件下的使用可用度和任务成功率。具体的仿真程序和流程分别如图6、7所示。

图6 仿真程序

图7 仿真流程
4 实例分析
以现役某型航空液压油泵车(简称“Y型油泵车”)为例,结合其实际使用保障数据,利用SIMLOX平台评估其保障能力,验证模型的适用性和有效性。
4.1 输入数据
Y型油泵车主要由Y-01、Y-02和Y-03三个功能子系统构成,各功能子系统又由若干个基本单元组成。由于篇幅有限,以下仅列举子系统一级的部分输入数据, 站点1、站点2和站点3分别表示3级保障组织,相关信息分别如表1-4所示。

表1 Y型油泵车的基础数据

表2 Y型油泵车的任务信息

表3 Y型油泵车的保障组织信息

表4 Y型油泵车的预防性维修信息
4.2 仿真结果分析
设置Y型油泵车的设计使用寿命131 400 h为仿真周期,仿真次数为100次,初始随机种子数为123 456 789,结果收集间隔期为24 h。图8为Y型油泵车的系统结构树,描述了装备—子系统—单元之间的层次关系以及各单元的装机数量。
图9为Y型油泵车的维修站点结构,描述装备(单元)进行修复性维修和预防性维修的组织关系。
图10为Y型油泵车的任务执行时间统计结果,可知其使用可用度为0.876。
图11为Y型油泵车的任务执行次数统计结果,可知其任务成功率为0.834 9。

图8 Y型油泵车的系统结构
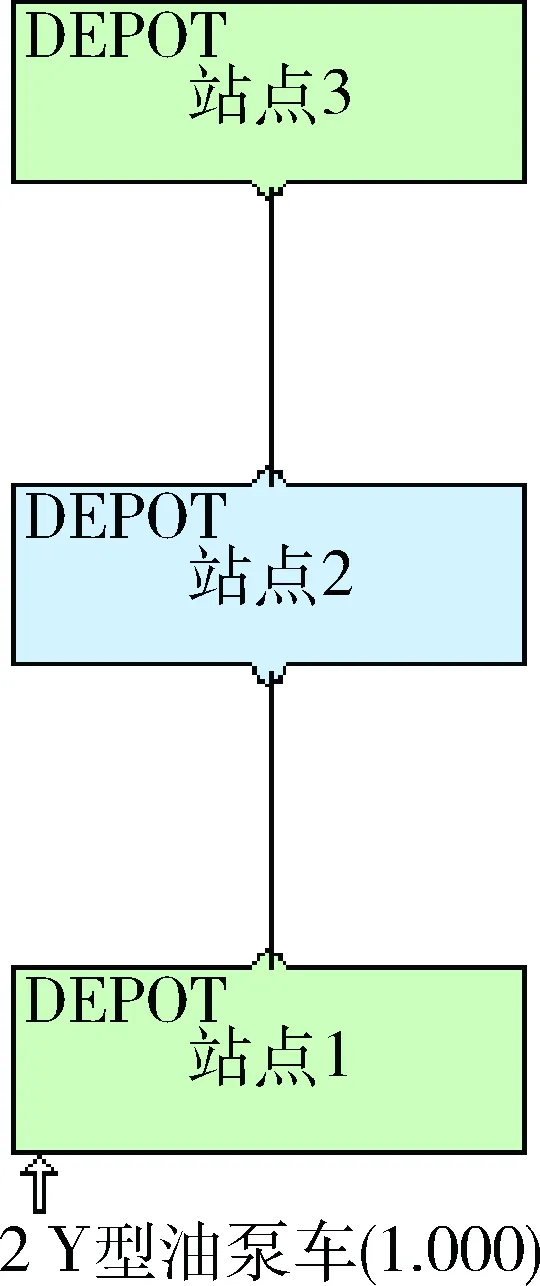
图9 Y型油泵车的维修站点结构

图10 Y型油泵车的任务执行时间统计结果

图11 Y型油泵车的任务执行次数统计结果
图12为Y型油泵车的备件短缺风险随时间变化情况,其备件短缺风险为0.188 6。

图12 Y型油泵车的备件短缺风险随时间变化情况
图13为仿真周期内Y型油泵车处于任务执行、任务等待、预防性维修和修复性维修等状态的统计结果。可以看出:在整个仿真周期内,对Y型油泵车保障能力影响较大的主要是装备发生故障后的备件短缺、预防性维修和备件在站点间的周转时间。

图13 仿真周期内Y型油泵车的状态统计结果
图14为各站点的备件短缺情况统计结果。可以看出:备件短缺多发生在站点1和站点2,这与实际情况是相吻合的,因为站点3既是顶层修理站点,又是Y型油泵车生产单位,其备件必然是充足的。
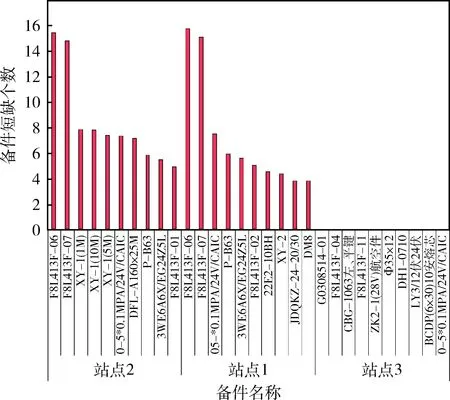
图14 各站点备件短缺情况统计结果
为了进一步验证模型的可行性,将各站点的备件初始库存数量各增加3个,预防性维修间隔期提高20%,预防性维修时间缩短30%,并提高故障件在站点1和站点2的修复概率,仿真结果如图15-17所示。可以看出:调整后,Y型液压油泵车的使用可用度和任务成功率均有显著提升,备件短缺风险明显降低。

图15 调整前后任务执行时间占比仿真结果对比

图16 调整前后任务执行次数占比仿真结果对比

图17 调整后备件短缺风险随时间变化情况
由此可见:为进一步提高Y型油泵车的保障能力,应采取以下4项措施:1)合理配置各站点的备品备件,尤其要有重点地提高站点1和站点2的备件初始库存种类和数量;2)提高预防性维修效率,缩短预防性维修时间;3)提高各级站点之间的备件调配能力,以减少备件在各级站点之间的周转时间;4)提高维修站点的维修能力,以提高故障件的修复效率。
5 结论
航空液压油泵车是战机飞行保障的重要地面保障装备,其组成结构复杂、单元众多,对其保障能力进行评估需要综合考虑实际保障过程、维修机理、备品备件配置等因素。笔者从任务角度出发,建立了包含结构模型、任务模型、保障资源模型、维修活动模型和仿真计算模型在内的航空液压油泵车保障能力评价模型,运用计算机仿真技术和SIMLOX平台对模型进行了实例检验,验证了模型的适用性,为航空液压油泵车保障能力评价提供了有效手段,可为航空液压油泵车的使用管理工作提供决策参考。
[1] 胡连桃,周俊.四站保障学[M].北京:蓝天出版社,2014:96-102.
[2] 杨为民.可靠性维修性保障性总论[M].北京:国防工业出版社,2004:117-120.
[3] 魏勇,徐廷学,顾钧元.面向任务的舰炮装备保障性评价指标研究[J].舰船电子工程,2010,30(1):61-65.
[4] 鱼静,王书敏,贾现录,等.基于作战任务的武器装备保障性研究[J].指挥控制与仿真,2014,36(4):82-85.
[5] 衡辉,魏勇,王新华,等.基于任务的潜用导弹武器系统保障性仿真评价[J].舰船科学技术,2013,35(2):110-114.
[6] 邵松世,魏勇,赵峰.基于任务的舰炮装备保障性评价仿真算法研究[J].系统仿真学报,2014,26(1):11-16.
[7] 夏旻,阎晋屯,刘磊.装备保障仿真模型框架及仿真平台研究[J].系统仿真学报,2006,18(2):210-213.
[8] 彭英武,李庆民,王睿,等.面向任务的装备保障仿真模型体系研究与应用[J].海军工程大学学报,2010,22(5):62-67.
[9] 邢联大,苏振华,张建荣.装备保障仿真中的任务建模研究[J].计算机与数字工程,2012,40(1):67-70.
[10] 魏勇,徐廷学,顾钧元.任务驱动的装备保障能力建模与仿真评价[J].火力与指挥控制,2011,36(10):61-65.

