面向满足率与利用率的通用备件优化配置方法

王俊龙，楼京俊，阮旻智，徐立

1. 海军工程大学 舰船与海洋学院，武汉 430033

2. 海军工程大学 兵器工程学院，武汉 430033

备件是装备开展维修保障工作的物质基础。在确定装备备件主要保障指标和备件配置方案制定过程中，会因为对备件保障效能评估指标的理解不够，导致在制定指标要求的时候出现相互矛盾的情况。一方面，希望备件配置数量越高越好，这样才能满足装备维修保障需求，提高备件供给效果；另一方面，希望备件利用率越高越好，避免出现“备而不用”的情况，提高备件利用效率。因此，在进行装备保障过程中，需根据实际情况，选取切实有用的备件保障效能评估参数，并制定可行的评估指标要求。

通用件是在不同类型或同类型不同规格的装备中互换性的部件单元。近年来，在装备建设过程中，装备的通用化、系列化、组合化程度的不断提高，通用备件的使用比例大幅上升，为保障部门对不同装备实施一体化保障提供了条件。由于通用件涉及的装备种类多、使用范围广、影响程度高，对不同装备通用产品备件进行统一考虑配置，相比单一装备自行配置来说，备件满足率与利用率都得到了相应的提高，因此，装备设计和保障部门对通用件的保障问题越来越关注。针对装备设计与保障部门对备件保障效能问题的关注，费广玉从国军标GJB-4355中满足率的统计定义入手，研究了备件满足率的意义，建立了以系统备件满足率为约束、其他参数为优化目标的备件配置优化模型。张志华等针对备件满足率的统计学定义，研究了单备件满足率和串联系统备件满足率的性质，给出了数学模型。阮旻智等从装备可用度出发，分析了装备可用度与系统备件满足率之间的关系，建立了任意结构系统的备件满足率模型。金正等针对舰船装备限寿件，研究了部件故障率服从指数分布的有寿件的更换规律，确定其保障期内的备件需求数量，建立舰船装备限寿件满足率评估模型。 Rodrigues和Yoneyama根据装备健康管理数据，在备件满足率约束下，以购置费用为优化目标开展备件配置方案优化。Topan和Lamghari等采用启发式算法计算备件配置情况，大大减少了装备的总停机时间，提高了备件保障效率，降低了备件购置成本。GJB1909A-2009给出了备件利用率的统计学定义，并没有给出备件利用率的具体数学表达式。应新雅等在任务时间确定情况下，建立了系统备件利用率评估模型，分析了系统备件利用率和单备件最低、最高利用率之间的关系。 李华等针对备件保障概率与备件利用率的关系进行了研究，并提出了一种备件利用率的估计方法。Ma等研究了不同工作周期内，随机需求情况下的通用件的配置问题，考虑了通用件成本结构、补充周期等因素。针对指数型部件备件利用率评估问题，徐立等针对寿命服从威布尔分布部件的通用件保障效能评估问题，采用等效的方法建立了不同寿命分布威布尔型部件的保障概率评估模型，并开展了指标约束下的备件配置方法研究。Turrini和Messiner根据工业部门和空军备件消耗数据，采用改进的Kolmogorov-Smirnov 拟合检验研究备件消耗的最佳拟合分布，预测备件需求情况。Boutselis和Mcnaught采用搭建仿真系统产生保障基础数据，在此基础之上，通过贝叶斯网络模型开展不同保障场景下的备件需求预测。 Zhu 等基于维修计划，提出了预测备件需求分布的简易方法和备件动态控制方法。 Sherbrooke 等面向多等级多层级维修保障系统，建立了可修复备件最优库存多级控制理论，以装备可用度为评价指标，实现了通用备件的优化配置方法研究。

本文针对通用件备件保障效能评估问题开展，建立通用件整体备件利用率和备件满足率评估模型。在此基础之上，开展备件评估指标约束下的备件优化配置研究。通过算例分析，研究常用备件评估指标备件满足率和备件利用率之间的关系。为装备论证、保障部门开展备件需求论证，制定备件配置方案提供理论支撑和决策支持。

1 基本描述及模型假设

1.1 保障过程描述

假设某通用件分别装备在台不同类型或者编号的装备中，已知该通用件观测周期内在装备中的计划工作时间为(1≤≤)，当该通用件发生故障后，采用换件维修的方式进行维修。由于工作时间和装备结构的差异，装备中通用件(1≤≤，为部件种类总数)的故障率会有差异，记为。现需在备件仓库中配置该通用件数量记为。在整个观测周期内，备件数量能够满足各装备备件需求的概率称为备件满足率。根据国军标GJB1909A—2009的定义，在规定的级别上和规定的时间内，实际使用的备件数与该级别实际拥有的备件数之比称为备件利用率。装备保障部门通常会对备件的保障效能即备件满足率和备件利用率提出指标要求，其中备件满足率为主要指标，一般会规定门限值，备件保障需使得其满足指标要求。在满足备件使用需求的基础之上，装备保障部门一般希望备件利用率越高越好。

1.2 模型假设

在装备保障过程中，为使得装备尽快排除故障投入使用，降低装备停机维修时间，装备现场通常对具备更换能力的故障部件进行换件处理。由于装备的科技水平和精密程度不断提高，在装备保障现场开展故障部件维修的效益较低，通常不进行故障部件的原位修复，而进行换件修理。除此之外，受生产过程影响，在装备部件批次采购之间，装备关重件的临时采购较为困难。因此，为了研究的方便，本文在建立模型和开展方案优化过程中做如下假设：① 装备故障维修仅进行换件维修，通用件均具备可更换属性；② 观测周期内不考虑通用件的补给；③ 故障后的部件不进行维修，无法作为完好件投入使用；④ 本文通用件备件寿命类型均服从指数分布。

2 通用件备件利用率模型

2.1 单类通用件备件利用率模型

假设部件故障率为，则若部件寿命类型服从指数分布，则在任务时间，部件发生的故障次数服从泊松分布，其公式为

(1)

对于同一类型装备，由于任务时间不尽相同，某一装备，在任务时间，装机数为，该装备上，部件发生故障次数服从泊松分布，其公式为

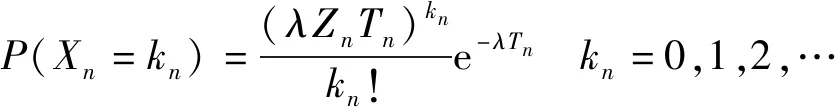
(2)

在观测周期内，装备1～，设部件在不同装备上的装机数为=[,,…,,…,]在不同任务期间=[,,…,,…,]条件下，该类部件发生故障次数的概率为

(3)

式中：表示装备序号。

根据卷积定理，可得个装备在任务周期内，发生次故障的概率为

[|(,)]=[=|(,)]*

[=|(,)]*…*[=

|(,)]*…*[=|(,)]

(4)

式中：“*”号表示卷积;装备总体在观测周期内的故障次数=++…+，同样的可求故障次数=++…。

当该类备件配置数量为时，由统计定义可知，备件利用率的统计量是一个离散型随机变量，与部件故障次数的关系式为

(5)

则对于装备总体而言，可得当某类备件配置数量为时，装备任务安排为=[,,…,,…,]，单个装备该类部件的装机数为=[,,…,,…,]时，在观测周期内备件利用率为

[|(,)]

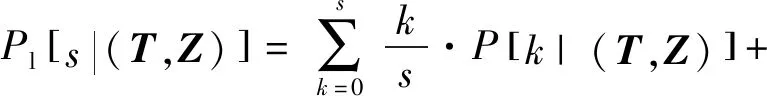
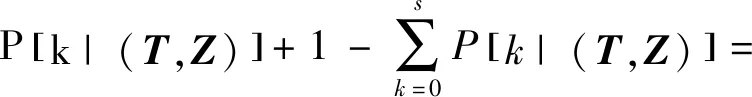
(6)

同时，在求得式(4)之后，可进一步求得该类部件的备件满足率模型

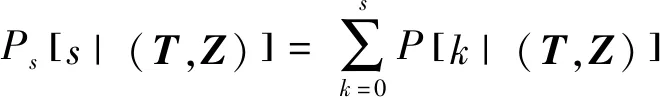
(7)

2.2 通用件整体备件利用率模型

2.1节搭建了单类备件利用率模型，在实际开展备件保障时，需要考虑装备不同种类备件总的利用率。根据国军标GJB1909A-2009的定义，备件利用率定义为：在规定的级别上和规定的时间内，实际使用的备件数与该级别实际拥有的备件数之比。假定装备总体共有类备件，第类备件配置数量为(为1～之间的正整数)，对于备件仓库而言备件总的配置方案为=[,,…,,…,]，则在观测周期内，不同部件总的备件利用率为

(8)

式中：l为第类部件的备件利用率。

也可求得部件总的备件满足率为

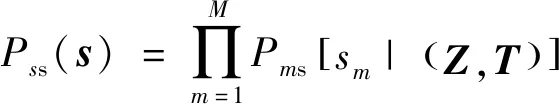
(9)

式中：s为第类部件的备件满足率。

3 备件优化模型及优化方法

3.1 备件优化模型

对于规定的保障任务，装备保障部门在制定备件配置方案时，需要考虑的是在备件能够满足备件需求的同时，所携带的备件能够尽可能地得到应用。因此备件满足率和备件利用率作为2个重要的指标，是备件筹措部门关注的重点。通常情况下，备件满足率作为备件保障效果的主指标，会设置一定的约束，使得其高于某一水平。与此同时，需要备件利用率尽可能地大。

可描述备件配置优化模型为，在备件满足率指标下0的前提下，使得备件利用率最大，即

3.2 备件配置方案优化算法

针对具体模型，可采用边际优化算法对优化模型进行求解，其算法流程如图1所示。

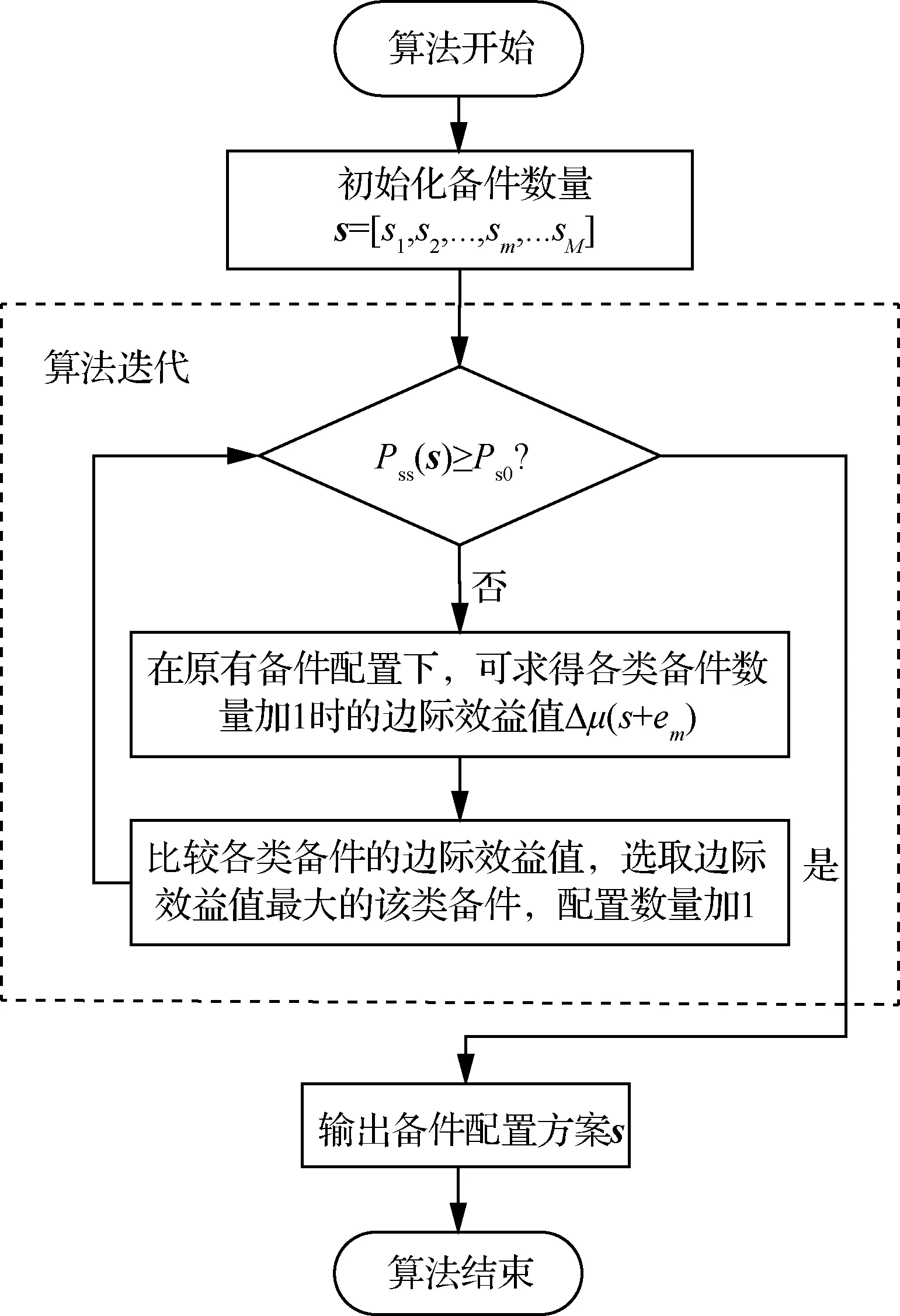
图1 备件配置方案优化算法流程Fig.1 Optimization algorithm flow of spare parts configuration scheme

备件数量初始化。由于备件总体备件满足率为各不同种类的部件联乘求得，因此，部件总体备件满足率低于各类备件满足率指标要求，初始状态下，求得各类备件在刚好达到备件满足率指标要求时的备件配置数量即为各类备件的初始配置数量。此时=[,,…,,…,]。

如果s()≥0迭代结束，输出此时的备件配置方案即为所求。如果s()<0则转步骤3。

在原有备件配置下，可求得各类备件数量加1时的边际效益值，如第类备件增加的边际数量为,第类备件的边际效益值为

比较各类备件的边际效益值，选取边际效益值最大的该类备件，配置数量加1，此时，如果s()≥0,迭代结束，输出此时的备件配置方案即为所求。如果s()<0,则转步骤3继续迭代。

4 算例分析

对于4类通用型部件，其在4个不同类型装备上的参数、装机数、任务时间等指标如表1所示。假设上级要求任务期间，部件总的备件满足率指标为0.9，现求观测周期内，不同类型的备件配置方案，使得在达到备件满足率指标要求的同时，备件利用率达到最大。

表1 各部件参数Table 1 Parameters of each component

对于不同故障率和装机数的部件1～部件4，随着备件数量的增加，其备件利用率和备件满足率之间的关系变化如图2～图5所示。

由图2～图5可知，随着备件配置数量的增加，备件满足率随之增加，与此同时，备件利用率随着备件配置数量的增加逐渐降低，二者具有一定的相关性。说明在进行备件配置过程中，要制定备件利用率和备件满足率“双高”的情况是很难实现的，这与2个指标的定义有关，备件满足率强调的是多备，这样才能满足装备不同情况下的备件需求；而备件利用率评价的是已配备备件的使用情况，在备件配置数量比较少时甚至当备件不能够满足装备使用需求时，备件利用率最高，此时配置的备件均能使用到，备件利用率为1，而随着备件配置数量的增加，备件配置也足够充足，此时，很有可能有的备件用不到的情况下已经能够满足装备的备件需求，此时备件利用率较低，出现“备而无用”的情况，过高的备件满足率水平会导致备件配置的浪费。观察图2～图5可知，备件满足率曲线和备件利用率的曲线大多相交于0.7～0.8之间。

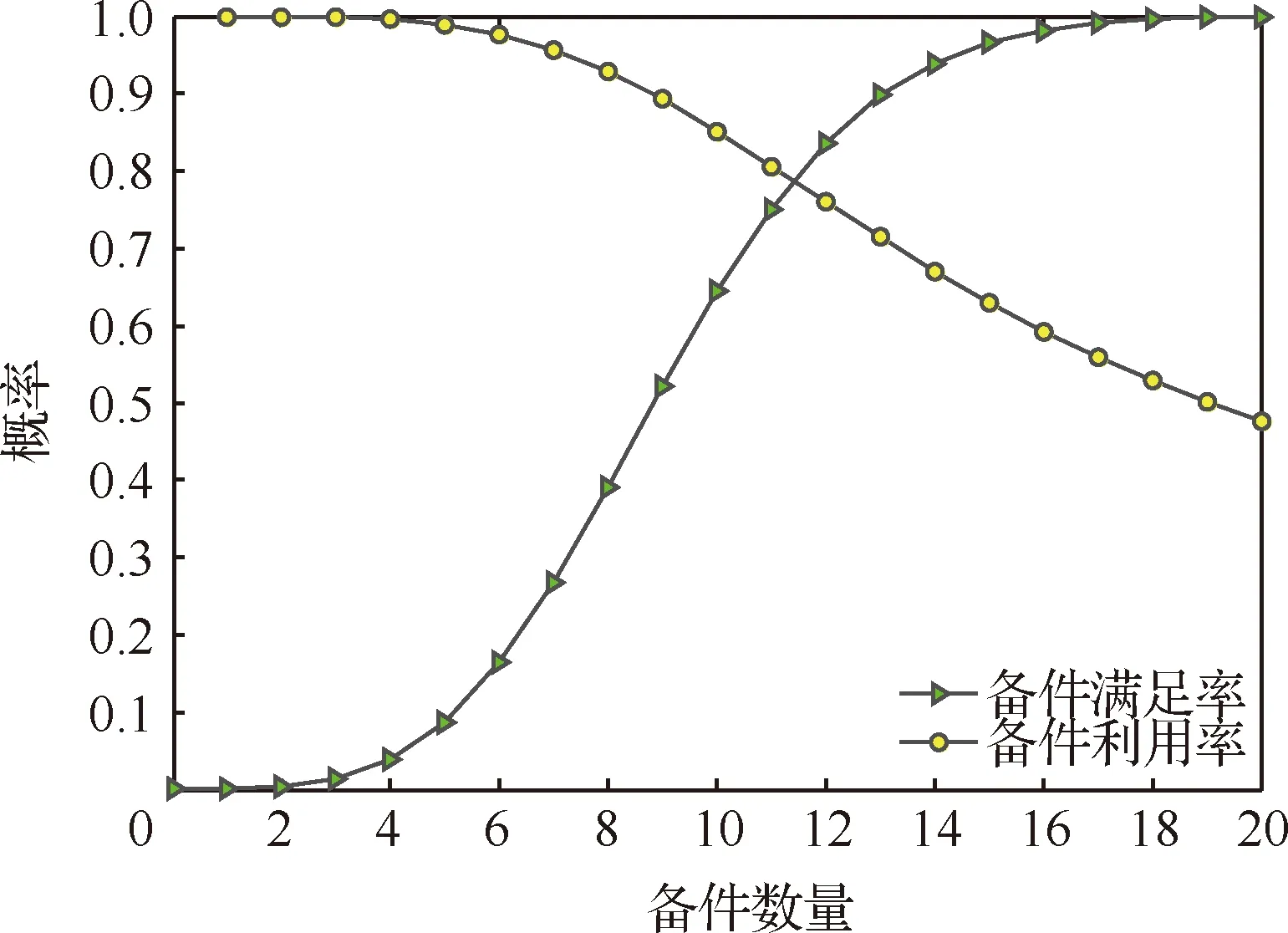
图2 部件1备件满足率和备件利用率的变化情况Fig.2 Changes in spare parts fill rate and spare parts utilization rate of Component 1

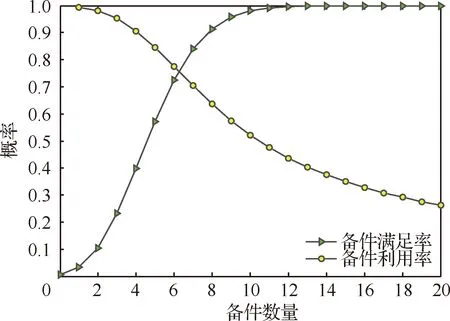
图3 部件2备件满足率和备件利用率的变化情况Fig.3 Changes in spare parts fill rate and spare parts utilization rate of Component 2

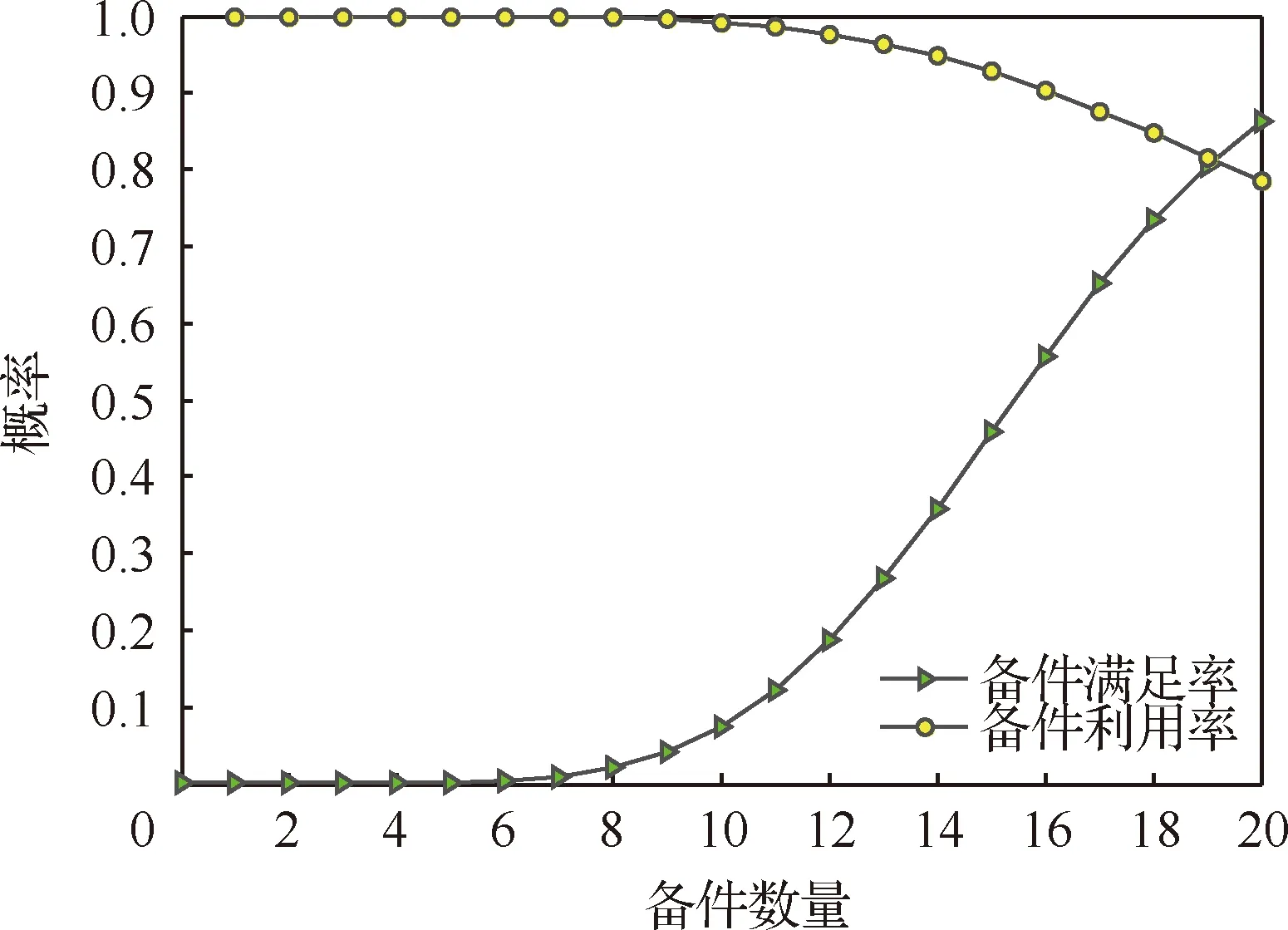
图4 部件3备件满足率和备件利用率的变化情况Fig.4 Changes in spare parts fill rate and spare parts utilization rate of Component 3

图5 部件4备件满足率和备件利用率的变化情况Fig.5 Changes in spare parts fill rate and spare parts utilization rate of Component 4

在备件满足率指标为0.85时开展备件优化配置，采用第3节的方法开展具体操作，此时，可计算各类备件的初始备件数量为(13,8,20,15)，每类部件的保障概率均为0.9以上。在此基础之上开展备件配置方案优化。其优化迭代过程如表2和图6所示。由表2可知，随着优化过程的开展，备件满足率随着备件配置数量的增加逐步增加。在备件满足率逐步增加的过程中，备件利用率随着备件数量的增加，备件利用率是逐步降低的。因此，在进行备件优化过程中，必须设置一个主要指标，根据第3节的论证结果可选取备件满足率为主指标，与此同时可要求备件利用率最大。

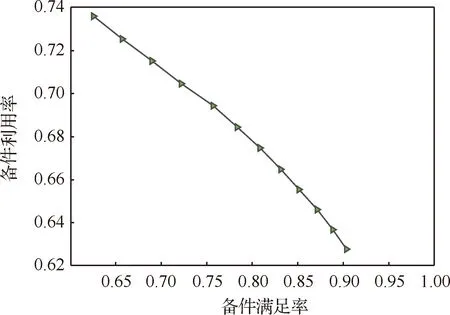
图6 优化迭代过程Fig.6 Optimal iterative process

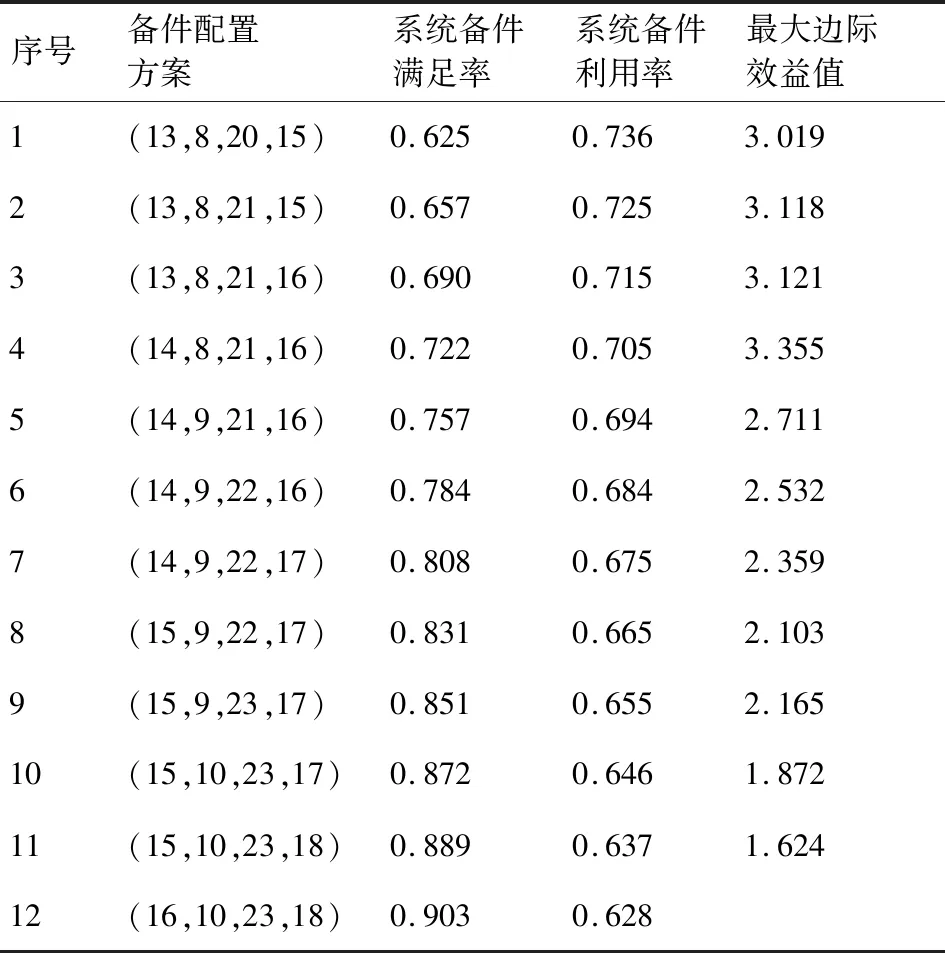
表2 优化迭代过程Table 2 Optimal iterative process

经过多次迭代，可求得优化后的备件配置方案为(16,10,23,18)，此时备件总体的满足率为0.903，备件利用率为0.628，满足指标要求。

5 结 论

1) 本文主要针对备件配置方案保障效能评估问题进行分析，建立了指数通用件整体备件利用率和备件满足率评估模型。在此基础之上，建立了备件满足率指标约束下的备件优化配置模型，并给出了通用备件优化配置方法。

2) 通过算例分析表明，随着备件配置数量的增加，备件满足率会随之增加，与此同时备件利用率会随之降低，在进行备件配置过程中，很难达到备件满足率和备件利用率双高的结果，过高的备件满足率会造成较大的备件浪费。

在进行备件配置过程中，需针对实际需求综合权衡备件满足率和备件利用率之间的关系，确定主要优化指标，提高备件使用效率，研究结果为开展备件需求论证，制定备件配置方案提供支撑。