有限可修复备件消耗规律预测方法

刘慎洋， 黄之杰， 卢 松， 魏东涛

(空军勤务学院航空四站系，江苏 徐州 221000)

由于我军高精尖武器装备列装部队时间短，基层部队使用所收集的备件消耗数据非常有限，现有的预测方法也不符合新装备的设计、使用和维修特点，迫切需要开展新装备备件消耗规律预测研究。

美陆军在计算装备备件消耗量时，充分考虑了备件的使用强度、使用时机、使用环境、使用场合、固有故障率以及备件损坏的敏感性等因素对备件消耗规律的影响[1]。美空军不仅验证了飞机发动机消耗的备件量与飞行小时数有关[2]，而且还发现其备件消耗量与飞行次数紧密相关。美海军采用移动平均法、指数平滑法等方法[3-4]预测备件消耗量，且将物流技术引入备件的管理中，改进备件消耗预测方法。我军针对装备备件消耗规律预测问题也开展了诸多研究[5-8]，取得了一定的成果。

总体来看，现有研究主要针对不可修复备件(简称“不修件”)开展备件消耗规律预测研究，针对有限可修复备件消耗规律的预测研究相对较少。如：文献[9-11]的作者分别建立了符合一定保障程度或保障概率条件的有限可修复备件需求预测模型,其中，陶小创等[11]研究发现我国装备研制部门和使用部门均将备件保障程度(保障概率)作为确定备件数量的指标要求，且在一定的备件保障程度(保障概率)的基础上预测备件需求量，如当某型装备备件保障程度(保障概率)达到95%以上时，其备件需求量的预测。由于备件消耗数量预测是研究装备正常工作期间实际耗损备件的数量，其可能小于需求量，也可能大于需求量，因此备件消耗量与需求量二者存在本质的区别。不修件消耗规律研究主要考虑单元发生故障后因更换而产生的消耗量或单元未发生故障因提前更换而产生的消耗量；而有限可修复备件消耗规律研究需考虑单元发生多次故障，且每次故障的时间都具有随机性的特点，因此可修复备件消耗规律预测难度更大。

由于可修复单元的工作时间长短在一定程度上影响装备的使用可用度，且该类备件的保障费用也较高，因此，笔者以有限可修复备件为研究对象，探索该类备件消耗规律的预测方法。

1 问题分析

装备单元是指组成装备的零部件、元器件、组合件、分系统和系统等的统称[12]。可修复单元是指故障或损坏之后通过采用经济可行的技术手段恢复其原有功能的装备单元。在实践中，装备可修复单元并不是可无限循环修复并使用的，绝大多数为有限可修复单元，可依据维修次数等限制条件对其备件消耗规律进行研究[13]。

当装备故障单元进行原件修复时，有如下3类维修状态：1)“修复如旧”，即修复单元的状态与故障前基本保持一致；2)“修复如新”，即修复单元的状态达到了新品状态；3)“不完全维修”，即修复单元的状态虽不能达到新品状态，但相对于维修前的状态有一定的改善，单元状态恢复至新、旧状态之间的某一状态[12]，是最常见的一种维修状态。

根据装备有限可修复单元的保障特点，若装备在使用期间发生功能故障，立即进行修复性维修，则其使用与修复过程如图1所示。

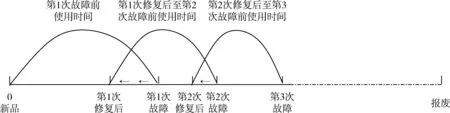
图1 有限可修复单元的使用与修复过程

由图1可以看出：当装备单元在使用过程中发生第1次故障后，可通过修复性维修使其役龄向前“回退”一段时间；当修复后的装备单元继续工作，发生第2次故障后，可通过修复性维修使其役龄又向前“回退”一段时间；此次类推，当装备单元的维修次数达到规定值，再发生故障时就不再继续使用和修复，必须进行换件修理，这时就产生1次备件消耗。

笔者以装备单元维修次数为约束条件，综合考虑装备数量、装备单元数量以及装备工作时间等备件消耗影响因素，建立有限可修复备件消耗规律预测模型。

2 模型构建

由于装备单元修复次数达到规定值后，其故障率会很高，继续修复效果较差，修复价值不大，因此维修时应限制装备单元修复次数，记其限定值为N。设装备单元从新品开始使用时的故障概率密度函数为f(t)，其可靠度函数为R(t)；在第j-1次修复后的故障概率密度函数为fj(tj)(1≤j≤N)，平均使用时间为θj；在第N次修复后的故障概率密度函数为fN+1(tN+1)，平均使用时间为θN+1；役龄“回退”因子为μ，即装备单元通过修复性维修可使其役龄向前“回退”平均维修间隔期的μ倍(0≤μ≤1)，即每次修复性维修可使单元“年轻”一段时间。则装备单元在第1次修复之前的平均使用时间为

(1)

由于装备单元在第j-1次修复时间点与第j次修复时间点之间的平均使用时间，与第j次修复时间点之前历次故障发生的时间均密切相关，考虑到历次故障的随机性、故障概率密度函数的不确定性特点，即第j次故障之前，历次相邻2次故障之间的实际使用时间ti(1≤i≤j)均为随机变量，因此通过对在j维空间取值范围内的j次故障的概率密度函数进行多重积分，可得装备单元在第j-1次修复时间点与第j次修复时间点之间的平均使用时间为

(2)

(3)

令j=N+1，依据式(2)、(3)，可求得装备单元在第N次修复时间点与第N+1次故障之间的平均使用时间θN+1。

若装备单元在N+1次故障后直接报废，则消耗1个备件，因此当预测一定时间内有限可修复备件的消耗数量时，需先计算出该单元报废之前的总平均使用时间。依据式(1)、(2)，对装备单元历次故障之前的平均使用时间进行累加，可得装备单元从新品开始使用到报废之前的总平均使用时间为

(4)

依据装备单元总平均使用时间，预计当装备工作T时间后该装备单元的备件消耗数量为

(5)

式中：W为装备数量;L为每台装备的单元数量(简称“单装用数”)。

对于μ，其取值存在如下3种情况：

1)当μ=1时，表示备件修复如新，则对第j-1次修复时间点之前历次故障的概率密度函数进行积分，结果均为1。因此，装备单元在任意2次修复时间点之间的平均使用时间均为

装备工作T时间后其单元消耗的备件数量预计值为

(6)

2)当μ=0时，表示备件修复如旧，由式(3)可知:装备单元在第j-1次故障与第j次故障之间的故障概率密度函数为

f1(t1)=f(t1)

。

装备工作T时间后其单元消耗的备件数量预计值为

(7)

3)当0<μ<1时，表示备件不完全维修，则依据式(5)可预计装备工作T时间后其单元消耗的备件数量。

3 示例分析

某单位配备某型地面空调装备10台，装备制冷系统的3类单元发生故障后在条件允许范围内均可进行修复性维修。其中：单元1和单元3为机械件，其故障规律分别服从正态分布和伽马分布；单元2为机电件，其故障规律服从威布尔分布。3类单元的单装用数、维修次数限定值、役龄“回退”因子以及单元从新品开始使用后的故障概率密度函数等基本信息如表1所示。需预测当每台装备平均工作2 000 h时，3类装备单元消耗的备件数量。

表1 3类单元的基本信息

依据式(1)、(2)、(4)，分别编程计算3类装备单元在不同使用阶段的平均工作时间及总平均工作时间，如表2所示。

表2 3类装备单元不同使用阶段的平均工作时间及总平均工作时间

将3类装备单元的相关参数值分别代入式(5)-(7)，可得每台装备平均工作T=2 000 h时，3类装备单元消耗的备件数量预计值分别为

因此，为满足未来2 000 h装备维修对3类装备单元备件的需求，建制单位应至少储备第1类备件20个、第2类备件27个、第3类备件15个。

4 结论

笔者针对有限可修复备件的消耗预测问题，将修复性维修的次数作为约束条件，运用数理统计方法，给出了装备单元在不同使用阶段的平均工作时间的计算方法，在此基础上，建立了有限可修复备件消耗规律预测模型。但本文提出的预测方法仅考虑了修复性维修的次数，下一步可参照该预测方法，系统性地将单元维修次数、单元故障率、单元维修费用和维修策略等多种因素综合起来作为约束条件，建立装备不同使用阶段的有限可修复备件消耗规律预测模型，为装备保障部门制定科学合理的可修复备件保障方案提供理论依据。

[1] COLCOMBE S J.Parts shortage are impacting operations and maintenance effectiveness：ADA391945[R]S.L.:s.n.,2001.

[2] KIM H E.Analysis of the reliability disparity and reliability growth analysis of a combat system using AMSAA extended reliability growth models:ADA443430[R].S.L.:s.n.,2006.

[3] BACHMAN T C.Reducing aircraft down for lack of parts with sporadic demand:ADA428159[R].S.L.:s.n.,2005.

[4] JOHN R.F.Improving the army’s management of reparable spare parts:ADA431882[R].S.L.:s.n.,2005.

[5] 卢庆龄,白盟亮,彭艳丽,等.基于灰色神经网络的装甲器材需求量预测[J].装甲兵工程学院学报,2011,25(6)：19-22.

[6] 冯辉,舒飞,朱建坤,等.车辆器材消耗的泊松预测模型研究[J].军事交通学院学报,2009,11(6)：29-31.

[7] 徐廷学,杜爱国,陈红.基于粗糙集和BP神经网络的飞航导弹备件消耗规律预测[J].海军航空工程学院学报,2012,27(5)：570-574.

[8] 曹军海,杜海东,陈小龙,等.基于平滑指数仿真优化的装甲装备器材消耗预测[J].系统仿真学报,2013,25(8)：1961-1965.

[9] 刘天华,张志华,梁胜杰,等.威布尔型可修备件需求量的解析算法研究[J].系统工程与电子技术,2012,34(5)：966-972.

[10] 陈砚桥,金家善,黄政.批量独立可修件的备件需求预测仿真算法[J].海军工程大学学报,2007,19(6)：79-81.

[11] 陶小创,郭霖瀚,肖波平,等.基于备件保障概率分配的备件需求量预测模型[J].兵工学报,2012,33(8)：975-979.

[12] 高崎.军械维修器材管理学[M].北京：国防工业出版社,2012：67-71.

[13] 甘茂治,康建设,高崎.军用装备维修工程学[M].北京：国防工业出版社,2005：243-244.