半群Tn(k)的正则性和Green关系

张传军，朱华伟

(1.广州市教育研究院，广东 广州 510006；2.深圳中学，广东 深圳 518025)

半群Tn(k)的正则性和Green关系

张传军1，朱华伟2

(1.广州市教育研究院，广东 广州 510006；2.深圳中学，广东 深圳 518025)

设Tn是[n]={1，…，n}上的全变换半群.对任意1≤k≤n，令

全变换半群；正则元；Green关系

1 预备知识

设S是半群，a，b∈S.如果a和b生成相同的主左理想，即S1a=S1b，则称a与b是L等价的，记为aLb或(a，b)∈L.如果a和b生成相同的主右理想，即aS1=bS1，则称a与b是R等价的，记为aRb或(a，b)∈R.如果a和b生成相同的主理想，即S1aS1=S1bS1，则称a与b是J等价的，记为aJb或(a，b)∈J.令H=L∩R，D=L∨R.众所周知，L，R，J，H和D都是半群S上的等价关系，这五个等价关系通常称为Green关系，是由J.A.Green[1]于1951年最先研究的.半群的Green关系研究对于半群代数理论的形成和发展具有极其重要的作用，是研究每一类半群的代数结构都要考虑的内容之一.

设[n]={1，2，…，n}并赋予自然序，Tn是[n]上的全变换半群.对任意1≤k≤n，令

Tn(k)={α∈Tn|∀x∈[n]，x≤k⟹xα≤k}，

则易验证Tn(k)是Tn的子半群且Tn(n)=Tn.

在半群研究的众多分支中，变换半群是半群代数理论中极为重要的一个研究方向，许多文献对全变换半群Tn各种子半群的Green关系做了很多工作.[2-8]本文考虑全变换半群Tn的一类新的子半群Tn(k)，讨论了它的正则性和格林关系L，R和D的等价刻画.

本文未定义的术语及记法参见文献[9].

2 半群Tn(k)的正则性

设S是半群.对于S中的元素a，若存在b∈S，使aba=a，则称a是S的正则元.若S中的每个元素都是正则元，则称S是正则半群.设x∈[n]，令

[1，x]={y∈[n]|1≤y≤x}.

对任意1≤k≤n，任取α∈Tn(k)，记：

△α(k)=im(α)∩[1，k]；

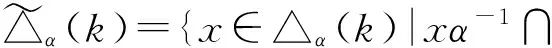
∏α(k)={x∈[n]|xα≤k}.

注2.1 本文假设n≥3且1≤k≤n.

证明 假设α是正则元，则存在β∈Tn(k)，使得α=αβα.任取x∈△α(k)，则

x=(xα-1)α=(xα-1)αβα=(xβ)α，

从而xβ∈xα-1.由x∈△α(k)可知x≤k，于是由β∈Tn(k)可得xβ≤k.故

xβ∈xα-1∩[1，k]，xα-1∩[1，k]≠∅.

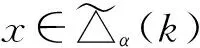
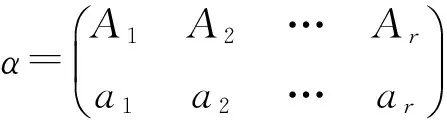
令

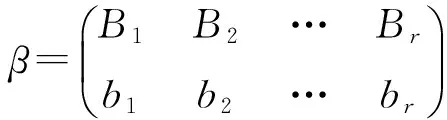
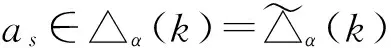
xβ=asβ=Bsβ=bs=minAs≤k.

其次，若x∈Bs{as}，则x∈As，于是minAs≤x≤k，从而

xβ=Bsβ=bs=minAs≤k.

定理2.2 设n≥3.则Tn(k)是正则半群，当且仅当k=1或k=n.

证明 若k≠1且k≠n，则k∈{2，…，n-1}.令

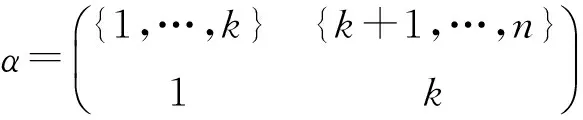
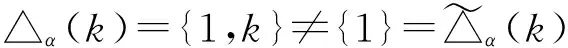
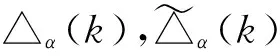
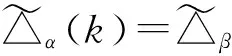
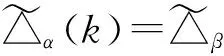
推论2.2 设α，β∈Tn(k)是正则元，且ker(α)=ker(β)，则∏α(k)=∏β(k).

证明 任取x∈∏α(k)，则xα≤k，从而xα∈△α(k)，再由定理2.1可得

故存在z∈[1，k]，使z∈(xα)α-1，即xα=zα.注意到x，z∈(xα)α-1.由ker(α)=ker(β)且β∈Sn(k)可得xβ=zβ≤k，从而x∈∏β(k).由x的任意性可得∏α(k)⊆∏β(k).同理可证∏β(k)⊆∏α(k).因此∏α(k)=∏β(k).

3 半群Tn(k)的Green关系

众所周知，在有限半群中D=J，因此本文仅讨论半群Tn(k)上的L，R和D关系.

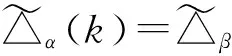
证明 假设(α，β)∈L，则存在δ，γ∈(Tn(k))1，使得α=δβ且β=γα，于是[n]α=([n]δ)β且[n]β=([n]γ)α，im(α)⊆im(β)且im(β)⊆im(α).故

im(α)=im(β)，△α(k)=△β(k).

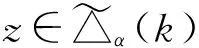
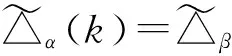
xδ=min(xα)β-1，x∈[n]，

xγ=min(xβ)α-1，x∈[n]，

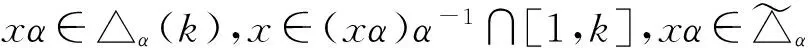
(xα)β-1∩[1，k]≠∅，

从而

xδ=min(xα)β-1≤k，δ∈Tn(k).

同理可证γ∈Tn(k)，因此(α，β)∈L.

定理3.2 设α，β∈Tn(k)，则(α，β)∈R，当且仅当ker(α)=ker(β)且∏α(k)=∏β(k).

证明 假设(α，β)∈R，则存在δ，γ∈(Tn(k))1，使α=βδ，β=αγ.任意(x,y)∈ker(α)，则xα=yα，于是xβ=(xα)γ=(yα)γ=yβ，从而(x，y)∈ker(β).由(x，y)的任意性可得ker(α)⊆ker(β).同理可证ker(α)⊇ker(β)，因此ker(α)=ker(β).

任意x∈∏α(k)，则xα≤k，于是由γ∈(Tn(k))1可得xβ=(xα)γ≤k，从而x∈∏β(k)，由x的任意性可得∏α(k)⊆∏β(k).任取x∈∏β(k)，则xβ≤k，于是由δ∈(Tn(k))1，xα=(xβ)δ)≤k，从而x∈∏α(k)，由x的任意性，∏β(k)⊆∏α(k).因此∏α(k)=∏β(k).

反之，假设ker(α)=ker(β)且∏α(k)=∏β(k).不妨设

令

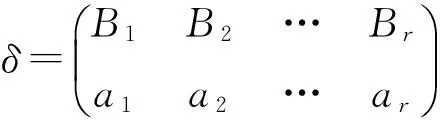
其中B1=A1∪{b1}，Bi=(Ai∪{bi}){b1，b2，…，bi-1}(i=2，3，…，r).则易知α=βδ.下证δ∈Tn(k).注意到

[n]=A1∪A2∪…∪Ar=B1∪B2∪…∪Br，

任取x∈[n]，若x≤k，则存在s∈{1，…，r}，使x∈Bs.(ⅰ)若x=bs，则Asβ=bs=x≤k，于是As⊆∏β(k)，从而由∏α(k)=∏β(k)可得As⊆∏α(k)，进而as=Asα≤k，xδ=Bsδ=as≤k.(ⅱ)若x∈Bs{bs}，则x∈As，于是由α∈Tn(k)可得as=xα≤k，从而xδ=Bsδ=as≤k.同理可以证明存在γ∈Tn(k)，使得β=αγ，因此(α，β)∈R.

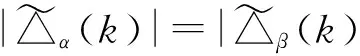
证明 假设(α，β)∈D，则存在γ∈Tn(k)，使得αLγ且γRβ.由定理3.1与3.2，

ker(γ)=ker(β)，∏γ(k)=∏β(k).

从而

|im(α)|=|im(γ)|=|[n]/ker(γ)|=|[n]/ker(β)|=|im(β)|.

再由im(α)=im(γ)，

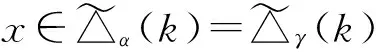
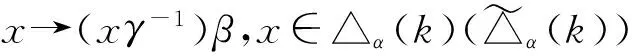
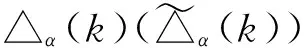
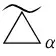
若xφ=yφ，则(xγ-1)β=(yγ-1)β，于是

xγ-1=yγ-1，x=(xγ-1)γ=(yγ-1)γ=y.

因此φ是单射.任取y∈△β(k)，则(yβ-1)β=y≤k，于是

yβ-1⊆∏β(k)=∏γ(k).

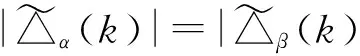
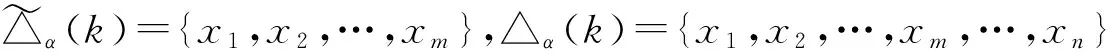
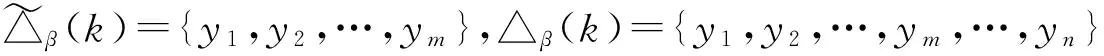
im(α)={x1，x2，…，xm，…，xn，…，xn+l}，

im(β)={y1，y2，…，ym，…，yn，…，yn+l}.

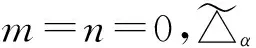
(yiβ-1)γ=xi，1≤i≤n+l，

则

im(α)=im(γ)，ker(γ)=ker(β)，yiβ-1=xiγ-1(1≤i≤n+l).

首先证明γ∈Tn(k).任取x∈[n]，若x≤k，则由β∈Tn(k)可得xβ≤k，从而存在yi∈△β(k)，使xβ=yi，即x∈yiβ-1.注意到1≤i≤n(因yi∈△β(k)={y1，…，yn})，由yiβ-1=xiγ-1，x∈xiγ-1，于是xγ=xi∈△α(k)，xγ≤k.因此γ∈Tn(k).

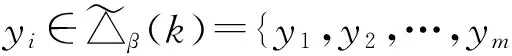
再次证明βRγ.任取x∈∏β(k)，则xβ≤k，xβ∈△β(k)，从而存在yi∈△β(k)，使xβ=yi，即x∈yiβ-1.注意到1≤i≤n(因yi∈△β(k)={y1，…，yn})，由yiβ-1=xiγ-1可得x∈xiγ-1，于是xγ=xi∈△α(k)，xγ≤k，即x∈∏γ(k).由x的任意性可得∏β(k)⊆∏γ(k).同理可证∏γ(k)⊆∏β(k).故∏β(k)=∏γ(k). 再由定理3.2知βRγ.

综上，αLγRβ，(α，β)∈D.

由推论2.1，2.2及定理3.1—3.3易得下面结论.

推论3.1 设α，β∈Tn(k)是正则元，则：

(1)αLβ，当且仅当im(α)=im(β)；

(2)αRβ，当且仅当ker(α)=ker(β)；

(3)αDβ，当且仅当|im(α)|=|im(β)|且|△α(k)|=|△β(k)|.

任取α，β∈Tn(n)，则显然△α(n)=im(α)且△β(n)=im(β)，从而|im(α)|=|im(β)|，当且仅当|△α(k)|=|△β(k)|.由定理2.2及推论3.4可得以下结论.

推论3.2 设全变换半群Tn(n)=Tn.对任意α，β∈Tn(n)，有：

(1)αLβ，当且仅当im(α)=im(β)；

(2)αRβ，当且仅当ker(α)=ker(β)；

(3)αDβ，当且仅当|im(α)|=|im(β)|.

[1] GREEN J A. On the structure of semigroups[J]. Ann Math，1951，54(2)：163-172.

[2] PEI H S. Regularity and Green’s relations for semigroups of transformations which preserve an equivalences[J].Communications in Algebra，2005，33(1)：109-118.

[3] PEI H S，ZOU D Y. Green’s equivalences on semigroups of transformations preserving order and an equivalence[J]. Semigroup Forum，2005，71(2)；241-251.

[4] PEI H S，SUN L，ZHAI H C. Green’s relations for the variants of transformation semigroups preserving an equivalence relation[J]. Communications in Algebra，2007，35(6)：1971-1986.

[5] SUN L，PEI H S. Regularity and Green’s relations for semigroups of transformations preserving orientation and an equivalence[J]. Semigroup Forum，2007，74(3)：473-486.

[6] DENG L Z，ZENG J W，XU B. Green’s relations and regularity for semigroups of transformations that preserve double direction equivalence[J]. Semigroup Forum，2010，80(3)：416-425.

[7] DENG L Z，ZENG J W，YOU T J. Green’s relations and regularity for semigroups of transformations that preserve reverse direction equivalence[J]. Semigroup Forum，2011，83(3)：489-498.

[8] DENG L Z，ZENG J W，YOU T J. Green’s relations and regularity for semigroups of transformations that preserve order and a double direction equivalence[J]. Semigroup Forum，2012，84(1)：59-68.

[9] HOWIE J M. Fundamentals of semigroup theory[M]. Oxford：The Clarendon Press，1995：1-349.

(责任编辑：李亚军)

Regularity and Green’s relation on the semigroupTn(k)

ZHANG Chuan-jun1，ZHU Hua-wei2

(1.Guangzhou Institute of Educational Research，Guangzhou 510006，China； 2.Shenzhen Middle School，Shenzhen 518025，China)

LetTnbe the semigroup of all full transformations of [n]={1，2，…，n}. For 1≤k≤n，letTn(k)={α∈Tn|∀x∈[n]，x≤k⟹xα≤k}.ThenTn(k) is a subsemigroup ofTn.The characterization of regular elements and Green’s relations are given on the semigroupTn(k).

full transformation semigroup；regular element；Green’s relation

1000-1832(2017)01-0038-05

10.16163/j.cnki.22-1123/n.2017.01.008

2015-10-19

国家高技术研究发展计划(863计划)项目(2015AA015408)；广东省教育科学“十一五”规划课题强师工程重点项目(2014ZQJK001)；贵州省科技平台及人才团队专项资金资助项目(黔科合平台人才[2016]5609).

张传军(1979—)，男，博士，副教授，主要从事数学自动化推理和半群研究；朱华伟(1962—)，男，博士，教授，博士生导师，主要从事数学教育和教育数学研究.

Tn(k)={α∈Tn|∀x∈[n]，x≤k⟹xα≤k}，则Tn(k)是Tn的子半群.刻画了半群GTn(k)的正则元的特征，并描述了该半群上的Green关系.

O 152.7 [学科代码] 110·2115

A