Bn上一类螺形映照子族的不变性

王朝君，崔艳艳

(周口师范学院数学与统计学院，河南 周口 466001)

Bn上一类螺形映照子族的不变性

王朝君，崔艳艳

(周口师范学院数学与统计学院，河南 周口 466001)

将Roper-Suffridge算子在Cn中单位球Bn上加以推广，讨论了α次强β型螺形映照在推广后的Roper-Suffridge算子下的不变性.从定义出发，利用双全纯映照的增长定理证明了推广后的Roper-Suffridge算子在一定条件下保持α次强β型螺形性.

双全纯映照；螺形映照；Roper-Suffridge算子

螺形映照[1]是多复变几何函数论中重要的映照类，在对螺形映照讨论的过程中，人们根据映照不同的几何特征引入了螺形映照的许多子族，如α次β型螺形映照[2]、α次殆β型螺形映照[2]以及α次强β型螺形映照[2].

1995年，Roper-Suffridge算子[3]的引入，使得可以由单复变函数中具有某些特殊几何性质的双全纯函数构造出多复变函数中相应的双全纯映照，于是许多学者结合Roper-Suffridge算子讨论了螺形映照的子族或扩充，证明了推广的Roper-Suffridge延拓算子在不同空间与不同区域上保持螺形映照子族的性质.[4-7]

2005年，Muir和Suffridge[8]将Roper-Suffridge延拓算子推广为

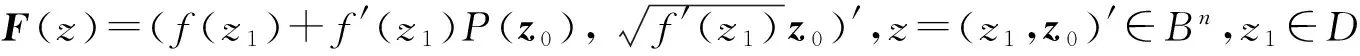
并证明了推广后的算子在一定条件下保持星形性和凸性.2008年Muir[9]将Roper-Suffridge延拓算子在复Banach空间单位球上进一步推广为

F(z)=(f(z1)+G([f′(z1)]γz0)，[f′(z1)]γz0)′.

本文在前人工作基础上将Roper-Suffridge延拓算子进行了改进，讨论了α次强β型螺形映照在推广后的Roper-Suffridge算子作用下的不变性.文中用D表示单位圆盘，Bn表示Cn中的单位球.

1 预备知识

下面将α次强β型螺形映照[2]的概念推广到Cn中单位球Bn上.

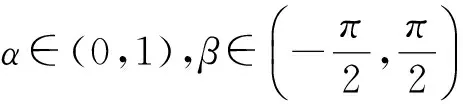
则称f(z)是Bn上的α次强β型螺形映照.

引理1.1[9]令P(z)是m次齐次多项式，DP(z)是P(z)在z点的Frechet导数，则DP(z)z=mP(z).

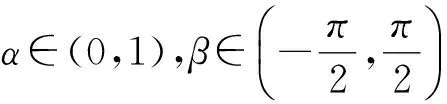
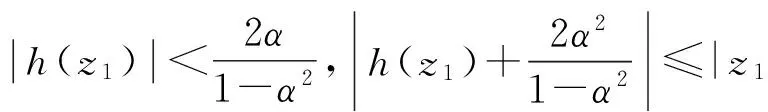
证明 令

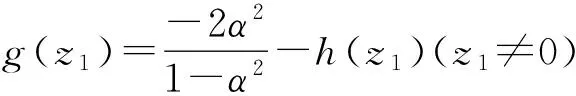
引理1.3[10]设f(z)是单位圆盘D上的正规化双全纯函数，则

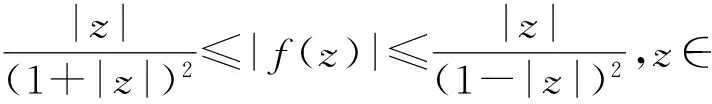
2 主要结论及其证明

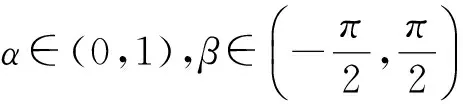
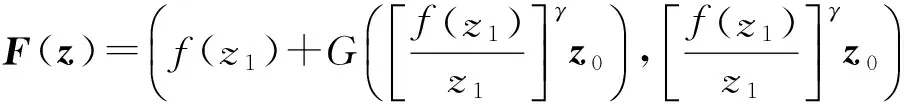
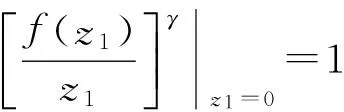
证明 由定义1.1，只需证明

(1)

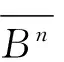
事实上，由F(z)的表达式及引理1.1知

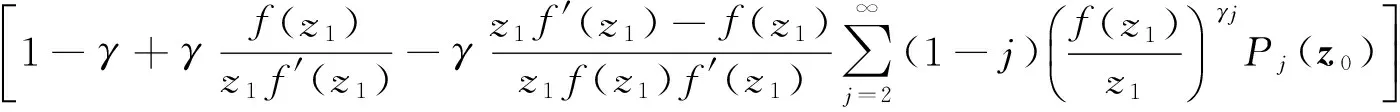
(2)

由于f(z1)是D上的α次强β型螺形函数，由定义1.1得

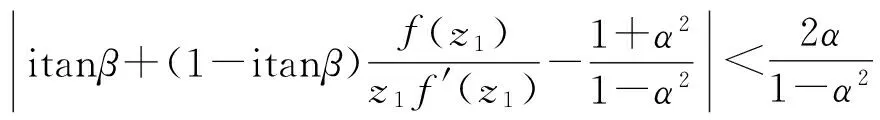
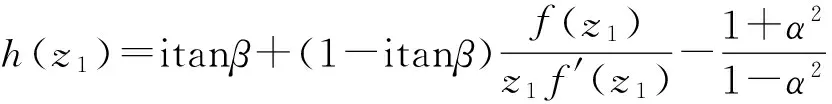
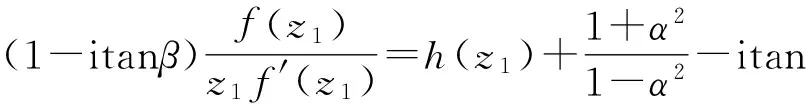
(3)

由(2)与(3)式知

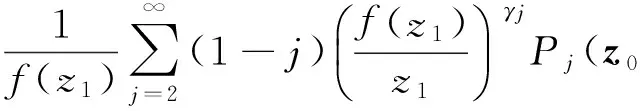
于是由引理1.2─1.3可得

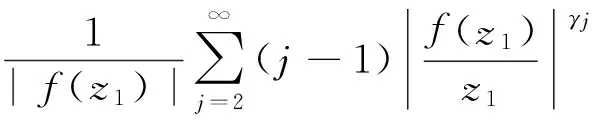
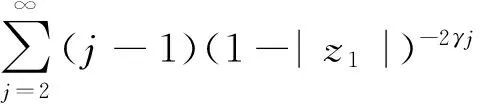
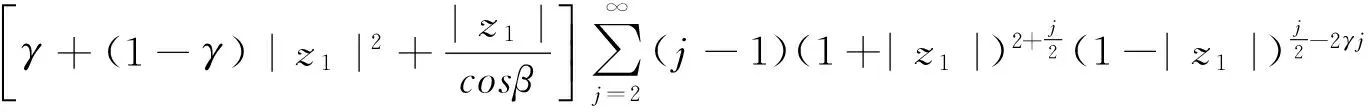
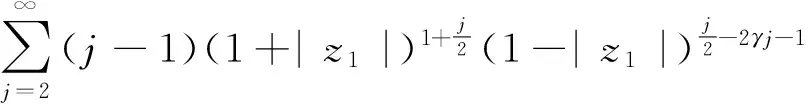
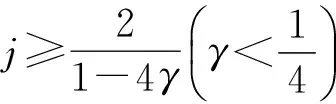
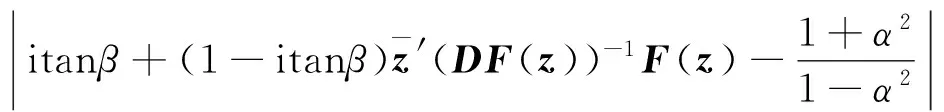
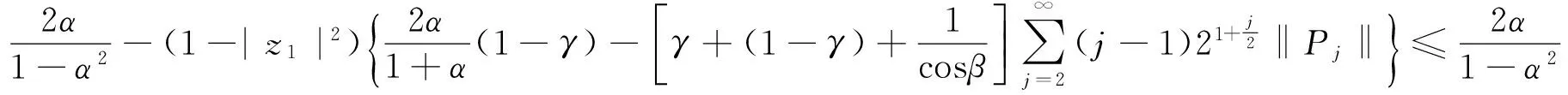
从而(1)式成立，定理得证.

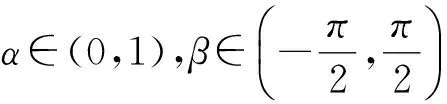
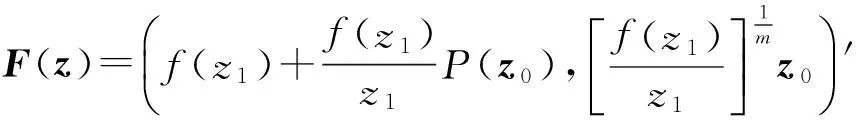
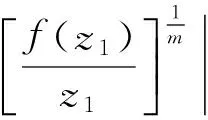
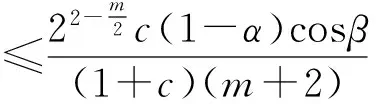
则F(z)是Bn上的强α次殆β型螺形映照.

注2.1 在定理2.1及推论2.1中令β=0则得到相应的关于强星形映照的结论.

[1] SUFFRIDGE T J.Starlikeness，convexity and other geometric properties of holomorphic maps in higher dimensions[J].Lecture Notes in Math，1976，599：146-159.

[2] 冯淑霞，刘太顺，任广斌.复Banach空间单位球上几类映射的增长掩盖定理[J].数学年刊，2007，28A(2)：215-230.

[3] ROPER K A，SUFFRIDGE T J.Convex mappings on the unit ball of Cn[J].J Anal Math，1995，65：333-347.

[4] 王建飞，刘太顺.全纯映射子族上改进的Roper-Suffridge算子[J].数学年刊，2010，31A(4)：487-496.

[5] LIU X S，FENG S X.A remark on the generalized Roper-Suffridge extension operator for spirallike mappings of typeβand orderα[J].Chin Quart J of Math，2009，24(2)：310-316.

[6] 刘名生，朱玉灿.有界完全Reinhardt域上推广的Roper-Suffridge算子[J].中国科学A辑，2007，37(10)：1193-1206.

[7] 冯淑霞，刘小松，徐庆华.Loewner链与推广的Roper-Suffridge算子[J].数学物理学报，2009，29A(6)：1601-1612.

[8] MUIR J R.A modification of the Roper-Suffridge extension operator[J].Comput Methods Funct Theory，2005，5(1)：237-251.

[9] MUIR J R.A class of Loewner chain preserving extension operators[J].J Math Anal Appl，2008，337(2)：862-879.

[10] DUREN P L.Univalent Functions[M].New York：Springer-Verlag，1983：57-58.

(责任编辑：李亚军)

The invarity of a subclass of spirallike mappings onBn

WANG Chao-jun，CUI Yan-yan

(School of Mathematics and Statistics，Zhoukou Normal University，Zhoukou 466001，China)

Generalizing the Roper-Suffridge extension operators on the unit ballBnin Cnand the invarity of strong spirallike mappingns of typeβand orderαunder the generalized Roper-Suffridge operators is discussed.From the definition and the distortion theorem of biholomorphic mappings，it is proved that the generallized operators keep strong spirallikeness of typeβand orderαunder some conditions.

biholomorphic mappings；spirallike mappings；Roper-Suffridge operator

1000-1832(2017)01-0029-04

10.16163/j.cnki.22-1123/n.2017.01.006

2015-04-30

国家自然科学基金资助项目(1271359，U1204618)；河南省自然科学基金资助项目(2011B110034)；河南省教育厅科学技术研究重点项目(17A110041)；河南省科技厅软科学项目(102400450003).

王朝君(1981—)，男，硕士，讲师，主要从事多复变函数论研究；通信作者：崔艳艳(1981─)，女，博士，副教授，主要从事多复变函数论研究.

O 174.56 [学科代码] 110·41

A