无界区域p(x)-Laplacian方程组全局弱解的存在性

赵彦军，姜淑珍，王增辉，车金星

(1.东北师范大学人文学院数学系，吉林 长春 130117；2.南昌工程学院理学院，江西 南昌 330099)

无界区域p(x)-Laplacian方程组全局弱解的存在性

赵彦军1，姜淑珍1，王增辉1，车金星2

(1.东北师范大学人文学院数学系，吉林 长春 130117；2.南昌工程学院理学院，江西 南昌 330099)

用弱连续法研究p(x)-Laplacian方程，在一定的假设下证明了p(x)-Laplacian方程组在无界区域上全局弱解的存在性.

弱连续法；p(x)-Laplacian方程组；全局弱解

0 引言

本文研究p(x)-Laplacian方程组全局弱解的存在性：

(*)

这里fi：Ω×RN→R是Caratheodory函数，Ω⊂Rn是无界区域.当p=2时，文献[1-2]中证明了此类非线性椭圆方程组弱解的存在性.对在无界区域上关于该方程组的讨论，由于缺少最大值原理和De Giorgi 类的估计，且拓扑度方法、变分法以及单调算子法失效，故使得问题的研究变得很困难.文献[3-4]中，马天和余庆余建立了弱连续法，这是研究微分方程解的存在性的一个有效工具.文献[5]中，赵敦和钟承奎用该方法证明了系统(*)在p(x)=2时，拉普拉斯方程组Dirichlet问题在无界区域上局部强解的存在性.本文将进一步应用弱连续法将文献[5]中的结果推广到无界区域p(x)-Laplacian方程组(*)上.

1 弱连续方法

设X、Y是两个Banach空间，且X是自反的，Y是可分的；L是一个线性空间，L在X与Y中分别稠密；Y1，Y2是任意两个Banach空间.

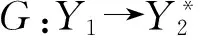
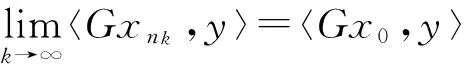
则称映射G是弱连续的.

定义2[4]设有界映射G：X→Y*.如果对任意xn(n=1，2，…)，x0∈X，若xn弱收敛于x0且满足：

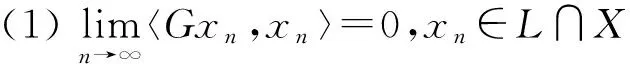
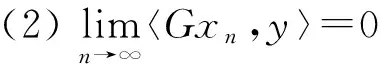
则称映射G是A-弱连续的.

定义3 设映射G：X→Y*.如果G限制在X的任意有限维子空间上是连续的，则称G是有限n-连续的.

弱连续方法的主要根据是下面的定理.

锐角原理[3-4]设映射G：X→Y*弱连续(或A-弱连续且有限n-连续).如果存在有界开集B⊂X，0∈B，使得

〈Gu，u〉≥0，∀u∈∂B∩L，

则算子方程Gu=0在X中至少存在一个解.

2 四个引理

设Ω为Rn中的开区域，E表示Ω上可测函数全体，p(x)∈E且满足

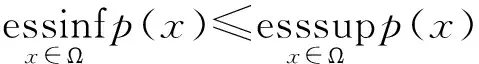
引理1 设Ω⊂Rn是具有锥性质的区域，{un}⊂W1，p(x)(Ω)，p-≥1.若un在W1，p(x)(Ω)中弱收敛于u0，则对任何有界子区域Ω0⊂Ω，un在Ω0上依测度收敛于u0.

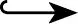
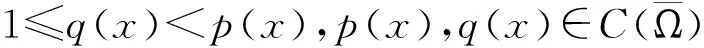
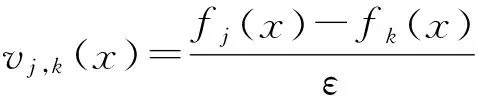
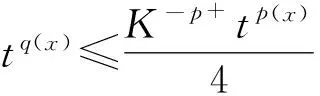
令

因{fn}依测度收敛，故存在整数N≥0，使得当j，k≥N时有

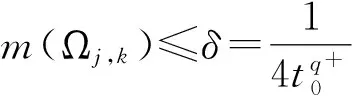
令

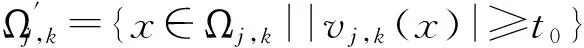
则

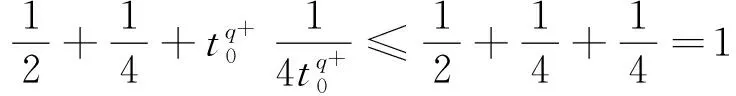
因此{fn}是Cauchy列，{fn}在Lq(x)(Ω)中收敛于ɡ，从而{fn}依测度收敛于ɡ.又由于fn依测度收敛于f0，从而f0=ɡ，即fn→f0在Lq(x)(x)上.

引理3 设f：Ω×Rl满足

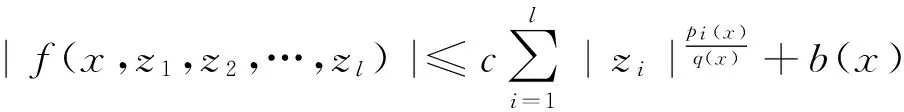
(1)

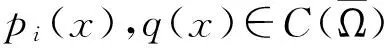
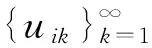
有界，ui0∈Lpi(x)(Ω)，对任意有界子区域Ω0⊂Ω，uik在Ω0上依测度收敛于ui0(i=1，…，l)，则对任意

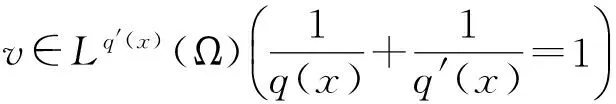
有

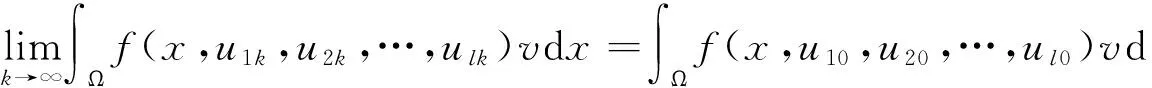
(2)

证明 根据(1)式，定义

f：Lp1(x)(Ω)×Lp2(x)(Ω)×…×Lpl(x)(Ω)→Lq(x)(Ω)，

〈fu，v〉=∫Ωf(x，u10，u20，…，ul0)vdx.

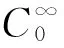
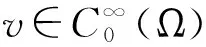
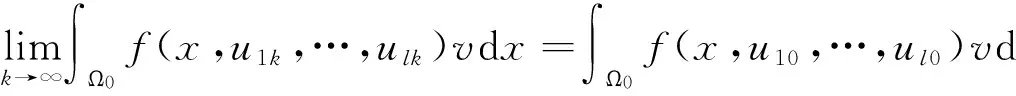
f(x，u1k，…，ulk)→f(x，u10，…，ul0)

引理4 设J∈C1(X，R)，

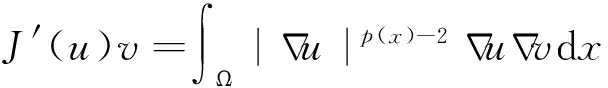
则算子J是凸泛函，且J′：X→X*是A-弱连续的.

证明 设xn(n=1，2，…)，x0∈X，xn弱收敛于x0且满足：

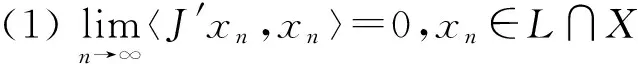
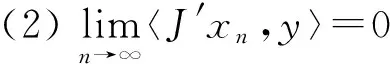
则当n→∞时有

〈J′xn-J′x0，xn-x0〉=

〈J′xn，xn〉-〈J′xn，x0〉-〈J′x0，xn〉+〈J′x0，x0〉→0.由文献[9]知J′是(S+)型算子，故在X中xn→x0，从而在X*中J′xn→J′x0.因此〈J′xn，y〉→〈J′x0，y〉，∀y∈X.

3 基本假设

设Ω⊂Rn(n≥2)是开区域，u1(x)，u2(x)，…，uN(x)，f1(x)，f2(x)，…，fN(x)是定义在Ω上的函数，且fi(x)(i=1，2，…，N)是Caratheodory函数.对问题(*)给出下面假设：

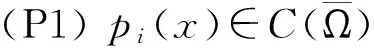
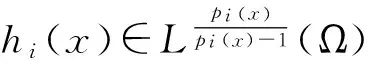
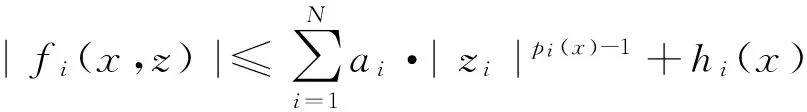
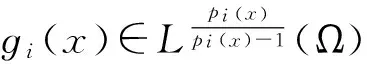
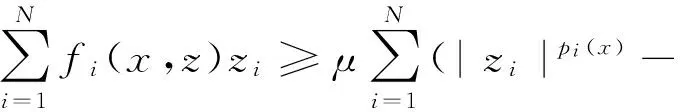
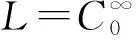
‖w‖Xi=‖w‖pi(x)+‖Dw‖pi(x).

令X=X1×X2×…×XN，则X在范数

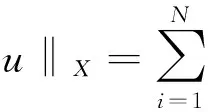
下是一个自反、可分的Banach空间.

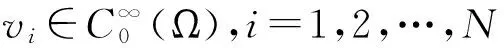
∫Ω[|Dui|pi(x)-2DuiDvi+fi(x，u1(x)，u2(x)，…，uN(x))vi]dx=0，

则称u=(u1，u2，…，uN)是方程组(*)的全局弱解.

4 主要结果及其证明

定理1 在假设(P1)—(P3)下，p(x)-Laplacian方程组(*)存在全局弱解u=(u1(x)，u2(x)，…，uN(x)).

证明 设u=(u1，…，uN)∈X.定义G：X→X*为

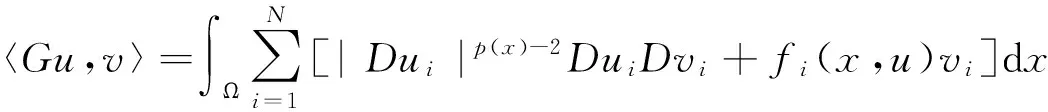
则

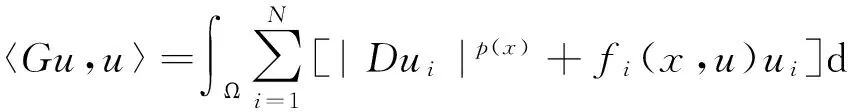
由假设(P3)和Young不等式，对任意ε>0，

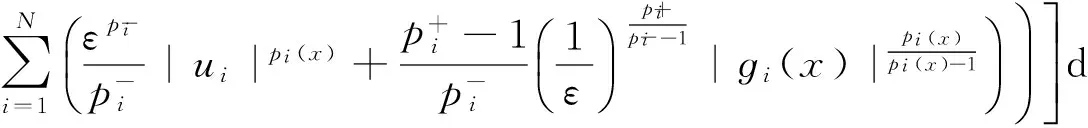
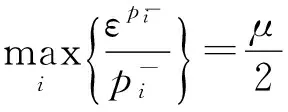
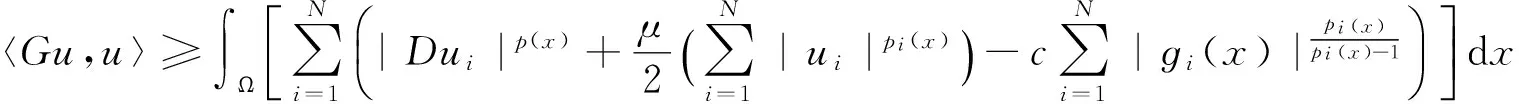
故对于球BR(0)⊂X，当R足够大时，对任意u∈∂BR(0)∩L，有〈Gu，u〉≥0成立.

下面证明G的A-弱连续性.由引理4，要证G的A-弱连续性，只要证明uik⇀ui0(i=1，…，N)时，

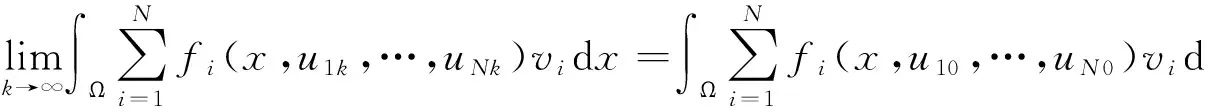
(4)

其中Fi是由fi定义的Nemytsky算子

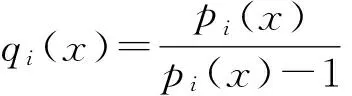
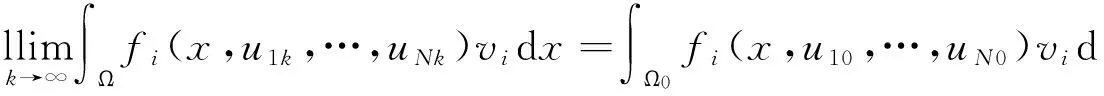
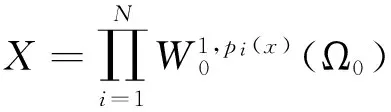
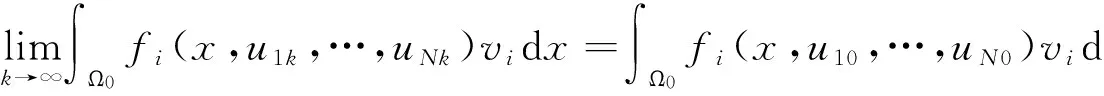
算子G的有限n-连续性是显然的.根据锐角原理，方程组(*)的全局弱解u=(u1(x)，u2(x)，…，uN(x))存在.

[1] MUSIELAK J.Orlicz spaces and Modular spaces[M].Berlin：Spring-Verlag，1983：151-163.

[2] LADYZENSKAJA O A，URAL’TZEVA N N.Linear and quasilinear elliptic equations[M].New York：Academic Press，1968：386-405.

[3] MA T，YU Q Y.The Keldys-Fichera boundary value problems for degenerate quasilinear elliptic equations of secong order[J]. Diff Int Eqns，1989(2)：379-388.

[4] MA T，YU Q Y.Nonlinear partial differential equations and weakly continuous method[M].Lanzhou：Lanzhou University Press，1990：118-213.

[5] ZHAO D，ZHONG C K.Existience of local strong solutions of elliptic systems on unbounded domain[J].Inter J Diff Eqns and Appl，2003(7)：115-121.

[6] FAN X L，ZHAO D.On the spacesLp(x)(Ω) andWk，p(x)(Ω)[J].J Math Appl，2001，263：424-446.

[7] FAN X L，SHEN J S，ZHAO D.Sobolev embedding theorems for spacesWk，p(x)(Ω)[J].J Math Anal Appl，2001，262：749-760.

[8] 赵敦，范先令.具p(x)-增长条件的2m阶椭圆型方程弱解的存在性[J].兰州大学学报(自然科学版)，2001，37(2)：1-6.

[9] FAN X L，ZHANG Q H.Existence of solutions forp(x)-Laplacian Dirichlet problem[J].Nonlinear Anal，2003，52：1843-1852.

(责任编辑：李亚军)

Existence of global weak solutions forp(x)-Laplacian systems in unbounded domain

ZHAO Yan-jun1，JIANG Shu-zhen1，WANG Zeng-hui1，CHE Jin-xing2

(1.Mathematics Department，College of Humanities and Sciences of Northeast Normal University，Changchun 130117，China; 2.College of Science，Nanchang Institute of Technology,Nanchang 330099，China)

Through the weakly continuous method，thep(x)-Laplacian systems are studied.The existence of global weak solutions ofp(x)-Laplacian systems in unbounded domain is given.

weakly continuous method;p(x)-Laplacian systems;global weak solution

1000-1832(2017)01-0015-05

10.16163/j.cnki.22-1123/n.2017.01.003

2015-07-20

国家自然科学基金资助项目(71301067).

赵彦军(1979—)，男，硕士，讲师，主要从事偏微分方程及其应用、应用时间序列分析与数据挖掘研究；通讯作者：王增辉(1956—)，男，教授，主要从事应用数理统计方法与生物数学研究.

O 177.92 [学科代码] 110·57

A