一类具有p-Laplace算子的二阶Hamilton系统周期解的存在性

万树园，王智勇

(南京信息工程大学数学与统计学院，江苏 南京 210044)

一类具有p-Laplace算子的二阶Hamilton系统周期解的存在性

万树园，王智勇

(南京信息工程大学数学与统计学院，江苏 南京 210044)

利用临界点理论中的极大极小方法，在一个新的局部渐近p-二次条件下研究了一类具有p-Laplace算子的二阶Hamilton系统周期解的存在性，得到了新的存在性定理.

p-Laplace系统；局部渐近p-二次；周期解；鞍点定理

1 主要结果

考虑系统

(1)

其中p>1，F：R×RN→R对所有u∈RN关于t是T-周期的(T>0).本文假设：

‖u‖∞≤d2‖u‖.

(2)

当p=2时，系统(1)退化为二阶Hamilton系统

(3)

近年来，许多学者利用变分法研究了系统(3)周期解的存在性，得到了一系列存在性和多解性结果.[2-10]但其局部渐近p-二次的情形很少被考虑过，受文献[3，6，8-10]的启发，本文利用鞍点定理，研究系统(1)中位势函数F(t，x)仅为局部渐近p-二次的情形，得到新的存在性定理.

定理1.1 若F满足假设(A)及以下条件：

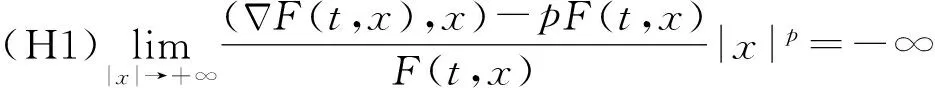
则系统(1)至少有一个T-周期解.

注1.1 (a) 由条件(H3)—(H4)可知定理1.1中的F(t，x)弱于通常的渐近p-二次条件：

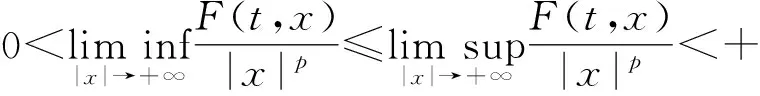
这里的(H3)，(H4)仅仅只是局部渐近p-二次的.

(b) 存在函数F满足定理1.1但不满足文献[2-10]中相关定理的条件.例如，令

其中

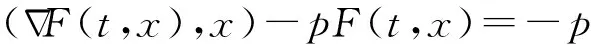
2 预备知识

由文献[1]易知φ是连续可微的，且φ的临界点对应系统(1)的T-周期解.

定义2.1[1]设X是实Banach空间，φ∈C1(X，R).如果{un}⊆X，φ(un)有界，φ′(un)→0(n→+∞)蕴含{un}有收敛子列，则称泛函φ满足Palais-Smale条件(简称PS条件).

定义2.2[1]设X是实Banach空间，φ∈C1(X，R).如果{un}⊆X，φ(un)有界，‖φ′(un)‖(1+‖un‖)→0(n→+∞)蕴含{un}有收敛子列，则称泛函φ满足Cerami条件(简称C条件).

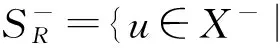
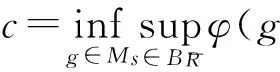
则当φ满足PS条件时，c为临界值.

注2.1 文献[11]表明，鞍点定理在更弱的C条件下仍然成立.

引理2.2 若假设条件(A)，(H1)—(H3)成立，则能量泛函φ满足C条件.

|φ(un)|≤L，(1+‖un‖)‖φ′(un)‖≤L.

(4)

由条件(H2)可知存在常数M1>0，使得对所有|x|≥M1，几乎处处的t∈[0，T]有

F(t，x)>0.

(5)

再结合条件(H1)，对∀β>0，存在常数M2>M1>0使得

(6)

令Ωn∶={t∈[0，T]||un(t)|≥M2}，根据假设(A)与(4)─(6)式有

(p+1)L≥(1+‖un‖)‖φ′(un)‖-pφ(un)≥(φ′(un)，un)-pφ(un)=

(7)

由此结合(2)与(5)式可得

(8)

利用假设(A)与(8)式有

(9)

另一方面，由(4)与(9)式，

(10)

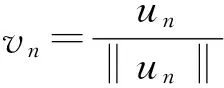
(11)

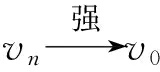
(12)

在不等式(10)两边同时除以‖un‖p，由β的任意性有

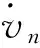
(13)

(14)

故当n→+∞时，|un(t)|→+∞，a.e.t∈[0，T]一致成立.结合(H2)，(H3)及Fatou引理，

(15)

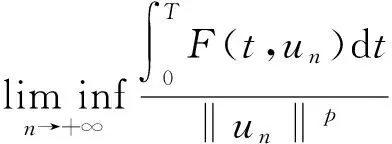
3 定理证明

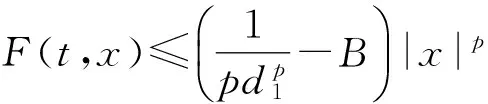
(16)

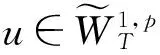
另一方面，∀u∈RN，利用(H2)，(H3)与Fatou引理，当|u|→+∞时有

即(ⅱ)也成立.

[1] MAWHIN J，WILLEM M.Critical point theory and Hamiltonian systems[M].New York：Springer-Verlag，1989：1-277.

[2] TANG C L，WU X P.Notes on periodic solutions of subquadratic second order systems[J].J Math Anal Appl，2003，285：8-16.

[3] JIANG Q，TANG C L.Periodic and subharmonic solutions of a class of subquadradic second-order Hamiltonian systems[J].J Math Anal Appl，2007，328：380-389.

[4] WANG Z Y，XIAO J Z.On periodic solutions of subquadratic second order non-autonomous Hamiltonian systems[J].Appl Math Lett，2015，40：72-77.

[5] FEI G H.On periodic solutions of superquadratic Hamiltonian systems[J].Electron J Differential Equations，2002，8：1-12.

[6] WANG Z Y，ZHANG J H，ZHANG Z T.Periodic solutions of second order non-autonomous Hamiltonian systems with local superquadratic potential[J].Nonlinear Anal，2009，70：3672-3681.

[7] TAO Z L，YAN S，WU S L.Periodic solutions for a class of superquadratic Hamiltonian systems[J].J Math Anal Appl，2007，331：152-158.

[8] SCHECHTER M.Periodic nonautonomous second order dynamical systems[J].J Differential Equations，2006，223：290-302.

[9] ZHANG Q，TANG X H.New existence of periodic solutions for second order nonautonomous Hamiltonian systems[J].J Math Anal Appl，2010，369：357-367.

[10] MA S W，ZHANG Y X.Existence of infinitely many periodic solutions for ordinaryp-Laplacian systems[J].J Math Anal Appl，2009，351：469-479.

[11] RABINOWITZ P H.Minimax methods in critical point theory with applications to differential equations[M].Providence：American Mathematical Society，1986：58-96.

(责任编辑：李亚军)

Existence of periodic solutions for a class of second-order Hamiltonian systems withp-Laplace

WAN Shu-yuan，WANG Zhi-yong

(School of Mathematics and Statistics，Nanjing University of Information Science & Technology，Nanjing 210044，China)

Using the minimax methods in critical point theory，the existence of periodic solutions for a class of second-order Hamiltonian systems withp-Laplace under a local asymptoticp-quadratic condition is considered and a new existence theorem is given.

p-Laplacian systems；local asymptoticp-quadratic；periodic solution；saddle point theorem

1000-1832(2017)01-0025-04

10.16163/j.cnki.22-1123/n.2017.01.005

2015-09-15

国家自然科学基金资助项目(11571176).

万树园(1992—)，女，硕士，主要从事非线性泛函分析研究；通信作者：王智勇(1979—)，男，博士，副教授，主要从事非线性泛函分析研究.

O 175.12 [学科代码] 110·41

A