状态依赖的随机干扰对一类流行病模型的影响

赵延辉，魏凤英

(福州大学数学与计算机科学学院，福建 福州 350116)

状态依赖的随机干扰对一类流行病模型的影响

赵延辉，魏凤英

(福州大学数学与计算机科学学院，福建 福州 350116)

研究了一类状态依赖的随机干扰对流行病模型的影响，讨论了具有饱和发生率的流行病模型的绝灭性及平稳分布.根据伊藤公式及构造的李雅普诺夫函数，证明了解的存在唯一性.主要研究结果说明：在适当的充分条件下疾病会灭绝；该模型存在一个遍历的平稳分布；利用傅里叶变换，得到了解在地方病平衡点渐近服从三维正态分布.数值模拟验证了所得结论的有效性.

随机扰动；流行病模型；饱和发生率；平稳分布；正态分布

0 引言

1992年，Mena-Lorca等[1]在假设种群密度并非恒定不变，且易感者具有常数输入率，部分感染者在恢复后具备免疫能力情形下，讨论了双线性传染率的流行病模型

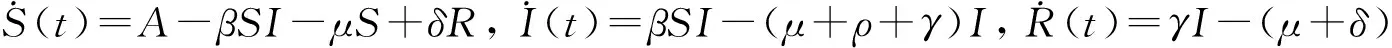
(1)

其中：S(t)，I(t)与R(t)分别代表t时刻易感者、感染者与恢复者的数量；A表示易感者的常数恢复率；β是疾病的传染率，βS表示单位时间内被一位感染者所传染的人数，βSI是单位时间内被所有感染者所传染的人数；μ表示平均自然死亡率；ρ是感染者的因病平均死亡率；δ是免疫丧失率；γ为感染者的恢复率.

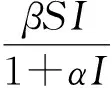
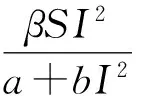
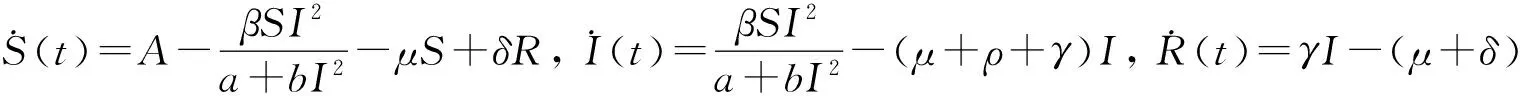
(2)

对模型(2)引入线性随机白噪声干扰项，即随机干扰是状态变量S，I，R的线性函数，得到干扰后的随机SIRS流行病模型

(3)

其中：B1，B2，B3为相互独立的一维标准的布朗运动；σ1，σ2与σ3分别是易感者、感染者与恢复者的随机噪声强度.

1 解的存在唯一性

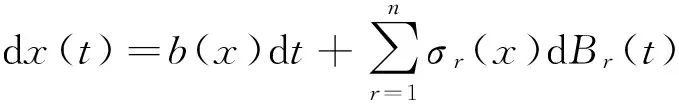
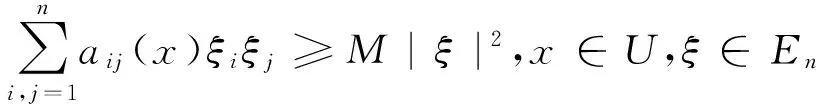
引理3[9]假设存在有界开集U⊂En且满足以下性质：

(1) 在开集U及其邻域中，扩散阵A(x)的最小特征值是非零的；

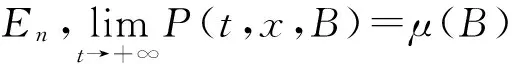
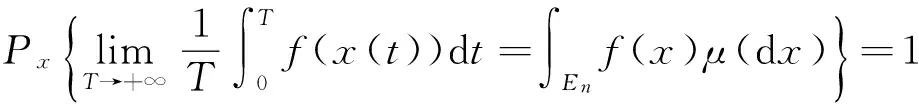
(4)

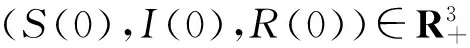
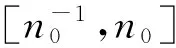
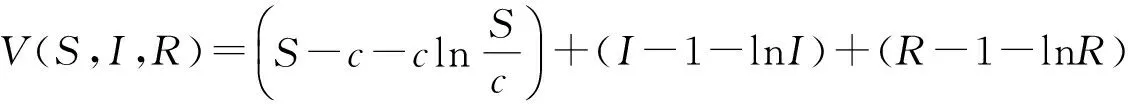
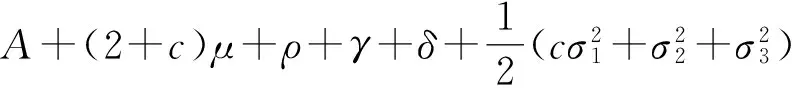
(5)

于是

dV(S，I，R)≤Mdt+σ1(S-c)dB1(t)+σ2(I-1)dB2(t)+σ3(R-1)dB3(t).

(6)

将上式两端从0到τn∧T积分后，再取数学期望得

EV(S(τn∧T)，I(τn∧T)，R(τn∧T))≤V(S(0)，I(0)，R(0))+MT<+∞.

对每一个ω∈Φn={τn≤T}，S(τn，ω)，I(τn，ω)，R(τn，ω)中至少有一个等于n-1或n，则

+∞>V(S(0)，I(0)，R(0))+MT≥E[IΦn(ω)V(S(τn∧T)，I(τn∧T)，R(τn∧T))]≥

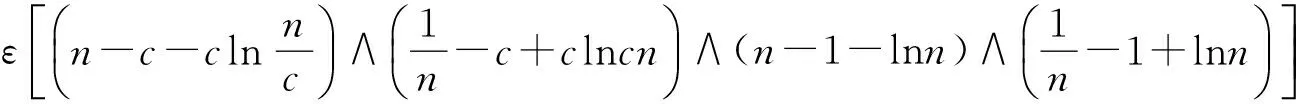
(7)

其中IΦn(ω)为Φn的示性函数.令n→+∞，有+∞>V(S(0)，I(0)，R(0))+MT≥+∞，矛盾.因此τ∞=+∞几乎处处成立，定理得证.

2 解的绝灭性及平稳分布

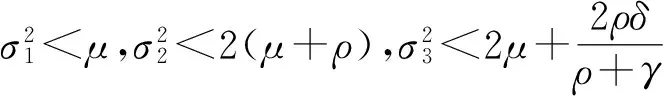
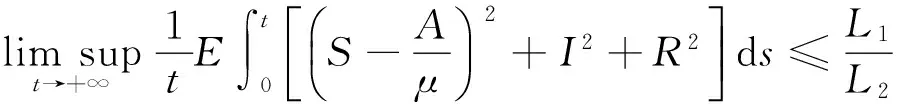
(8)

其中

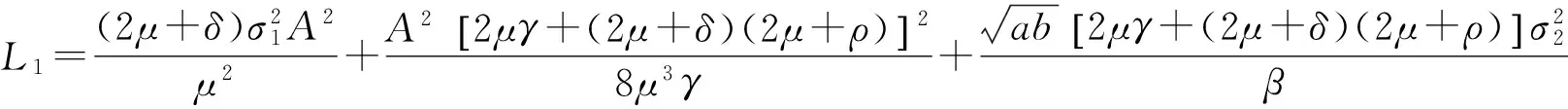
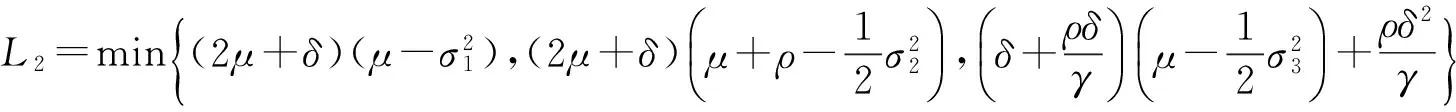
(9)

定义C2-函数

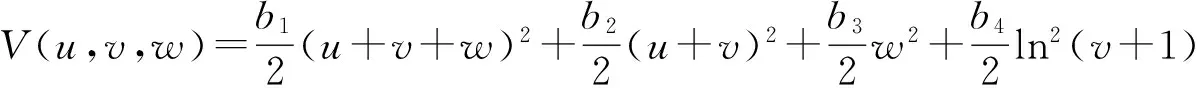
b1V1+b2V2+b3V3+b4V4，

(10)

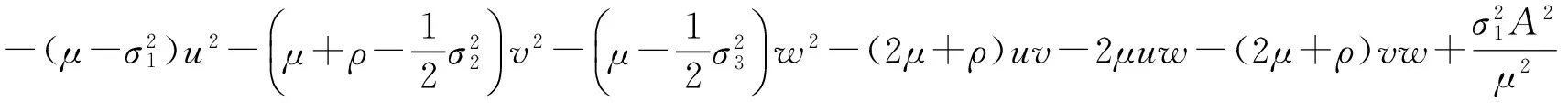
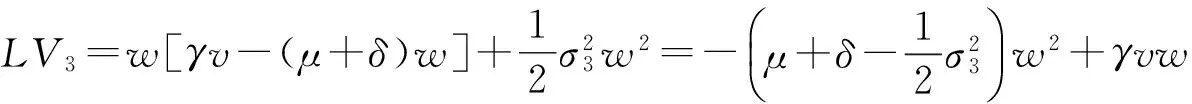
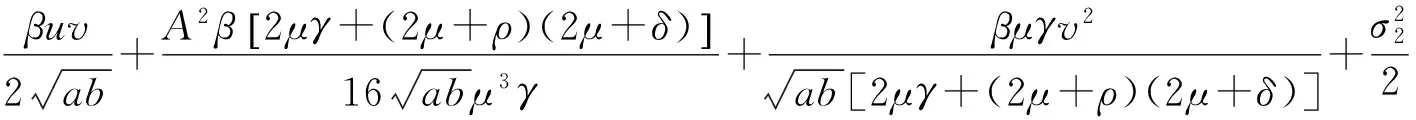
(11)

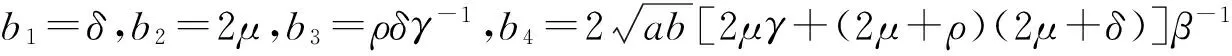
-L2(u2+v2+w2)+L1，

(12)

从而

dV≤[-L2(u2+v2+w2)+L1]dt+udB1(t)+vdB2(t)+wdB3(t).

(13)

对上式两边从0到t积分再取数学期望有

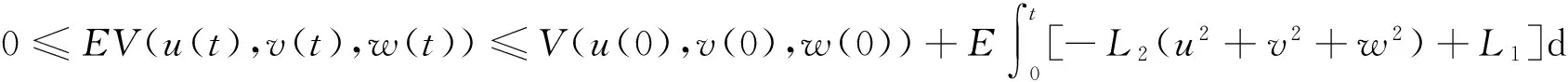
(14)

故

(15)

定理3 假设(S*，I*，R*)是模型(2)的地方病平衡点.若

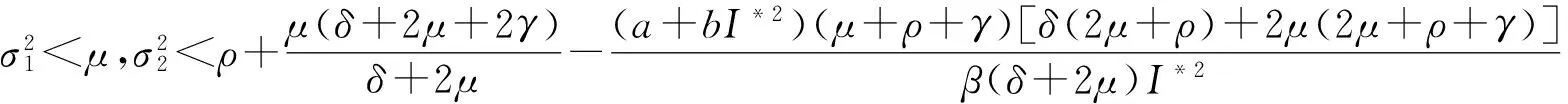
(16)

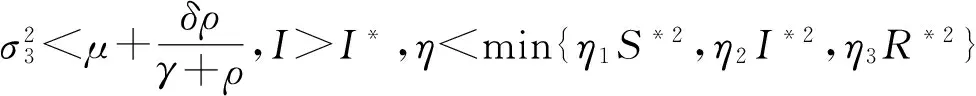
则模型(3)存在遍历的平稳分布.其中

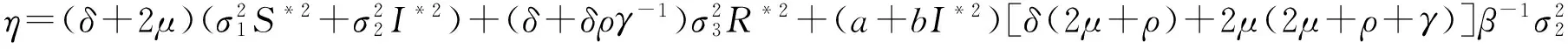
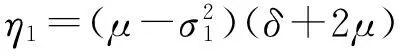
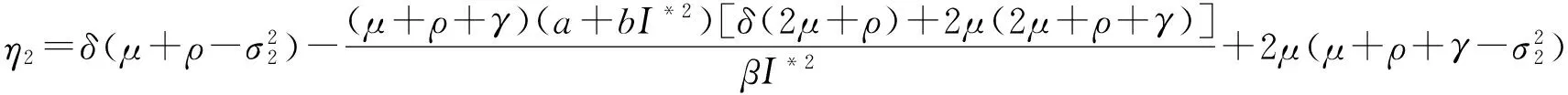
(17)

证明 由于(S*，I*，R*)是模型(2)的地方病平衡点，满足

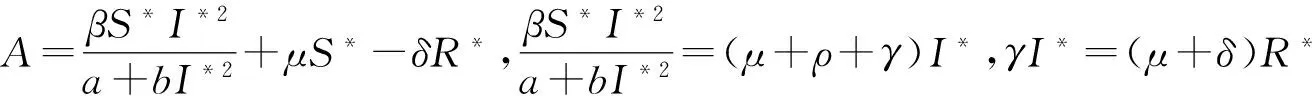
定义C2-函数

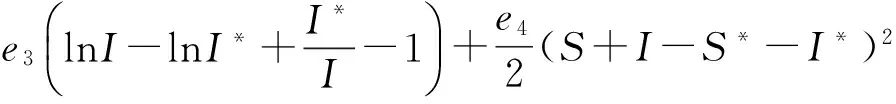
(18)

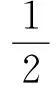
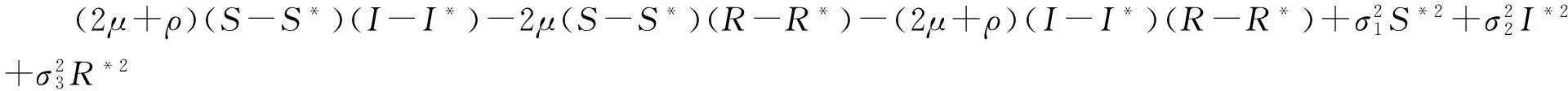
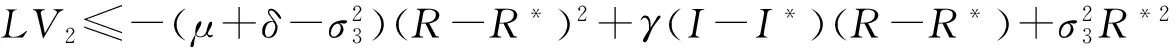
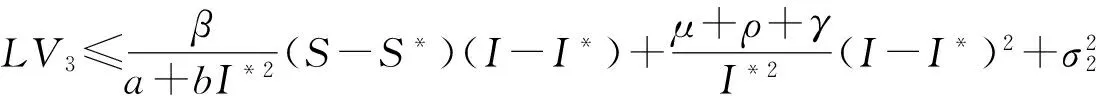
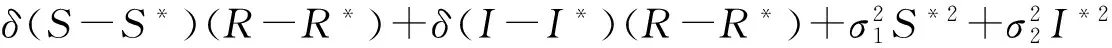
(19)

取e1=δ，e2=δργ-1，e3=β-1(a+bI*2)[δ(2μ+ρ)+2μ(2μ+ρ+γ)]，e4=2μ，则由(17)式得

LV≤-η1(S-S*)2-η2(I-I*)2-η3(R-R*)2+η.

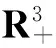
定理4 若模型(2)的地方病平衡点(S*，I*，R*)是稳定的，则模型(3)的解(S，I，R)渐近服从三维正态分布N((S*，I*，R*)，C(S，I，R)(0)).

证明 模型(3)简记为(dS，dI，dR)T=g(S，I，R)dt+σ(S，I，R)dB(t)，在地方病平衡点(S*，I*，R*)泰勒展开，又由于偏差S-S*，I-I*，R-R*不大，且σ1，σ2，σ3是较小的噪声强度，所以σ1(S-S*)，σ2(I-I*)，σ3(R-R*)较小，忽略高阶项，得到近似模型

df=[g(S*，I*，R*)+g′(S*，I*，R*)f]dt+σ(S*，I*，R*)dB(t).

(20)

其中f=(S-S*，I-I*，R-R*)T，σ(S*，I*，R*)=diag(σ1S*，σ2I*，σ3R*)，

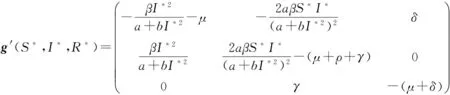
由于(S*，I*，R*)是稳定的，所以g(S*，I*，R*)=0，g′(S*，I*，R*)<0，从而方程(20)退化为三维Ornstein-Uhlenbeck过程

df-g′(S*，I*，R*)fdt=σ(S*，I*，R*)dB(t)，

(21)

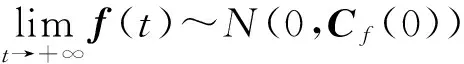
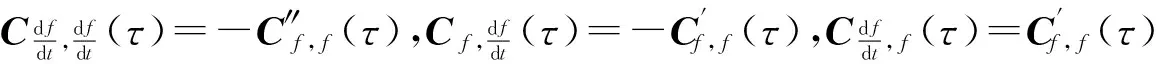
(22)

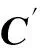
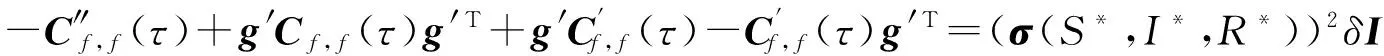
(23)

-(iω)2Sf(ω)+g′Sf(ω)g′T+iωg′Sf(ω)-iwSf(ω)g′T=(σ(S*，I*，R*))2.

(24)

由于g′的所有特征值都具有严格的负实部，所以g′±iωI是可逆矩阵，于是

Sf(ω)=(g′-iωI)-1(σ(S*，I*，R*))2[(g′+iωI)T]-1.

(25)

将上式作傅里叶逆变换，并取τ=0，得到方差矩阵

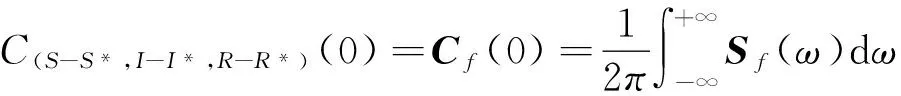
(26)

故Cf(0)=C(S，I，R)(0).

3 数值模拟

利用Milstein高阶方法[10]，得到离散化方程组

(27)

其中ξi，k(i=1，2，3，k=1，2，3，…，n)为独立高斯随机变量N(0，1).

在模型(3)中，取初值(S(0)，I(0)，R(0))=(5，3.5，1.5)，及参数

A=2，β=0.01，a=1.5，b=0.5，μ=0.03，δ=0.74，

ρ=0.45，γ=0.35，σ1=0.013，σ2=0.001，σ3=0.05.

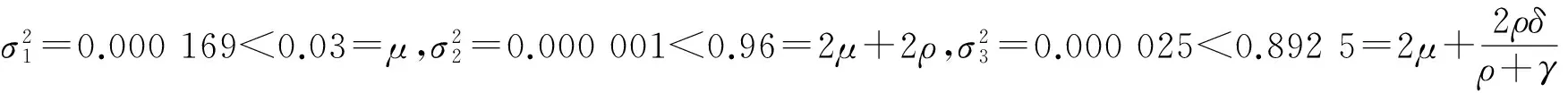
取模型(3)的初值(S(0)，I(0)，R(0))=(2.4，1.2，0.5)，k=10 000，t=200，参数A=45，β=0.07，a=0.02，b=0.085，μ=0.3，δ=0.95，ρ=0.65，γ=0.24，σ1=0.025，σ2=0.008，σ3=0.024.则定理3的条件成立，因此模型(3)的解在地方病平衡点周围振荡，并渐近服从三维正态分布N((S*，I*，R*)，C(S，I，R)(0))，这说明疾病将流行.

[1] MENA-LORCA J，HETHCOTE H W.Dynamic models of the infectious disease as regulator of population sizes[J].Journal of Mathematical Biology，1992，30：693-716.

[2] BROWN G C，HASIBUAN R.Conidial discharge and transmission efficiency of Neozygites floridana：an entomopathogenic fungus infecting two-spotted spider mites under laboratory conditions[J].Journal of Invertebrate Pathology，1995，65(1)：10-16.

[3] RUAN S G，WANG W D.Dynamical behavior of an epidemic model with a nonlinear incidence rate[J].Journal of Differential Equations，2003，188(1)：135-163.

[4] JIANG D Q，YU J J，JI C Y，et al.Asymptotic behavior of global positive solution to a stochastic SIR model[J].Mathematical and Computer Modelling，2011，54(12)：221-232.

[5] 赵亚男，王宇，夏兰，张晓颖.随机SIQS传染病系统的灭绝性和遍历性[J].吉林大学学报(理学版)，2013，51(6)：1081-1084.

[6] LAHROUZ A，OMARI L.Extinction and stationary distribution of a stochastic SIRS epidemic model with non-linear incidence[J].Statistics & Probability Letters，2013，83(4)：960-968.

[7] GARD T C.Introduction to stochastic differential equations[M].New York：Marcel Dekker，1988：35-55.

[8] ZHU C，YIN G.Asymptotic properties of hybrid diffusion systems[J].SIAM Journal on Control and Optimization，2007，46(4)：1155-1179.

[9] KHASMINSKII R.Stochastic stability of differential equations[M].Alphen：Sijthoff and Noordhoff，1980：43-93.

[10] HIGHAM D J.An algorithmic introduction to numerical simulation of stochastic differential equations[J].Siam Review，2001，43(3)：525-546.

(责任编辑：李亚军)

Impact of random perturbations with state-dependent on an epidemic model

ZHAO Yan-hui，WEI Feng-ying

(College of Mathematics and Computer Science，Fuzhou University，Fuzhou 350116，China)

This paper focuses on the impact of random perturbations with state-dependent on an epidemic model.The extinction and the stationary distribution of the epidemic model with a saturated incidence are discussed.By means of Ito’s formula and constructing Lyapunov functions，the existence and uniqueness of a global positive solution is investigated.The main results declare that the disease will die out under some sufficient conditions.And the model admits a stationary distribution with ergodic property and the solution asymptotically follows a three-dimensional normal distribution around the endemic equilibrium according to Fourier transform.Some numerical simulations are carried out to show the efficiency of our main results.

random perturbations；epidemic model；saturated incidence；stationary distribution；normal distribution

1000-1832(2017)01-0009-06

10.16163/j.cnki.22-1123/n.2017.01.002

2015-11-20

国家自然科学基金资助项目(11201075)；福建省自然科学基金资助项目(2016J01015).

赵延辉(1990— )，女，硕士，主要从事随机微分方程研究；魏凤英(1976—)，女，博士，教授，主要从事生物数学与随机微分方程研究.

O 211 [学科代码] 110·64

A