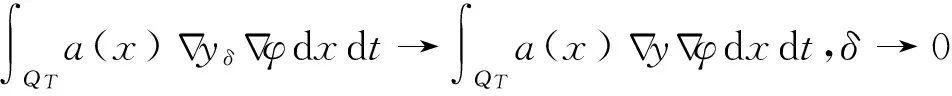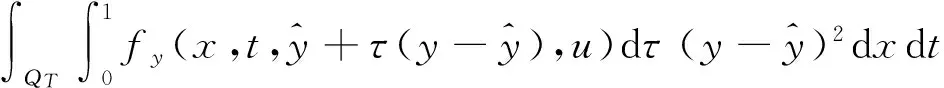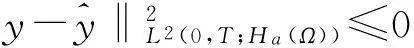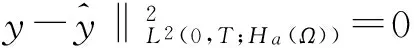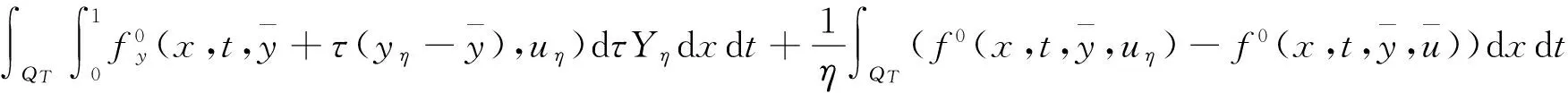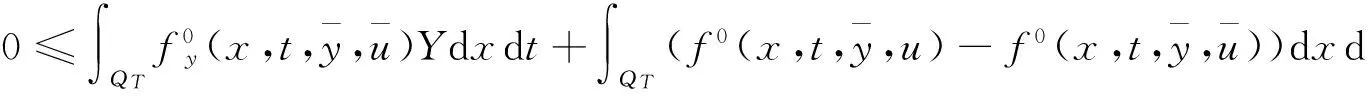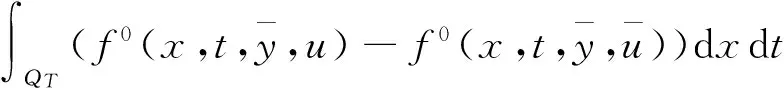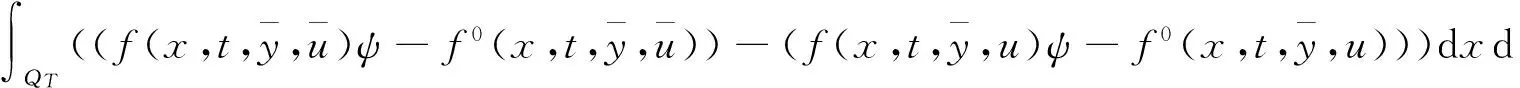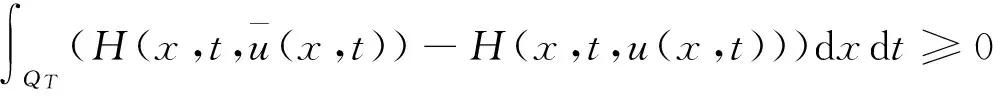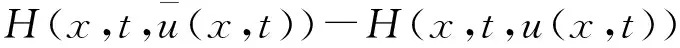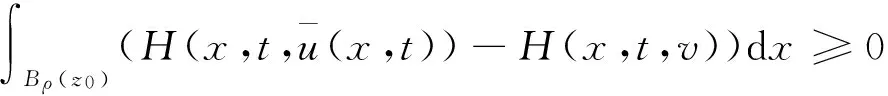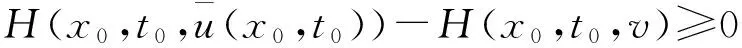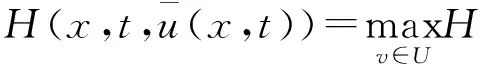一类由退化半线性抛物方程所支配系统的最优控制问题
张 敬,高 夯
(1.齐齐哈尔大学理学院,黑龙江 齐齐哈尔 161006;2.东北师范大学数学与统计学院,吉林 长春 130024)
一类由退化半线性抛物方程所支配系统的最优控制问题
张 敬1,高 夯2
(1.齐齐哈尔大学理学院,黑龙江 齐齐哈尔 161006;2.东北师范大学数学与统计学院,吉林 长春 130024)
研究了一类由退化半线性抛物方程所支配的分布参数系统的最优控制问题.当退化点集的测度为零时,利用正则化方法和变分思想,得到了该分布参数系统最优控制的Pontryagin最大值原理.
退化半线性抛物方程;最优控制;正则化方法;变分思想;Pontryagin最大值原理
1 问题的提出与主要结果
最优控制理论是发展迅速的现代控制理论的核心内容之一,其主要实质是在满足一定约束条件下,寻找容许的控制规律使规定的指标泛函达到最小值.自从集中参数系统的最优控制理论建立后,众多学者就致力于把它推广到分布参数系统:李训经和雍炯敏[1]对一类分布参数系统最优性条件进行了讨论;E.Casas,J.P.Raymond等学者研究了各类抛物方程支配系统的最优控制问题,得到了系统最优控制的存在性或必要条件.[2-8]由于在渗流理论、生物化学以及生物群体动力学等领域都提出了非线性退化抛物方程,研究这类退化方程支配系统的最优控制问题更具现实意义.S.M.Lenhart和雍炯敏[9]研究了一类带有逻辑增长的退化抛物方程的最优控制问题,得到了方程解的存在唯一性、正则性以及系统最优控制的存在性.本文所研究的是文献[10]中提及但退化情形不同的抛物方程支配系统的最优控制问题.
本文讨论如下的退化半线性抛物方程支配的系统
(1)
其中QT=Ω×(0,T),Ω⊂Rn(n≥2)是具有光滑边界∂Ω的有界区域,∂QT=∂Ω×(0,T),控制函数u(x,t)∈U,U为Rm中的有界闭集.
假设:

(P2)f:QT×R×U→R满足:f(·,y,u)在QT上有界可测;f(x,t,·,·),fy(x,t,·,·)在R×U上连续,且存在常数L>0使得
|fu(x,t,y,u)|≤L,∀(x,t,y,u)∈QT×R×U.
由于方程具有退化性,问题(1)可能不存在古典解,需讨论其广义解.
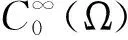
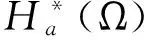

引入容许控制集
Uad={u:QT→U|u(·)在QT上可测}.
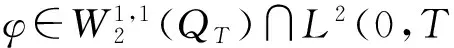
成立.
定理1 假设(P1)与(P2)成立.若y0(x)∈L2(Ω),则对任意的u(·)∈Uad,问题(1)存在唯一的广义解y(·)∈L2(0,T;Ha(Ω))∩C(0,T;L2(Ω)).
在Uad上定义泛函
J(u(·))=∫QTf0(x,t,y(x,t),u(x,t))dxdt.
进一步假设:
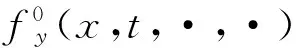


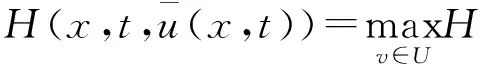
成立,其中
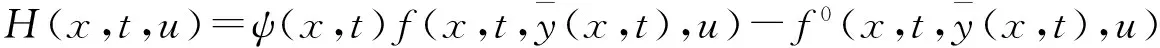
而ψ(·)∈L2(0,T;Ha(Ω))∩C(0,T;L2(Ω))满足
(2)
2 状态方程的变分
对δ>0,考虑问题(1)的正则化问题
(3)
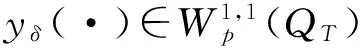

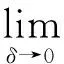
(4)
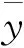
(5)

(6)
(5)与(6)相减得

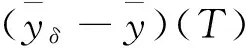
利用Cauchy不等式并整理得
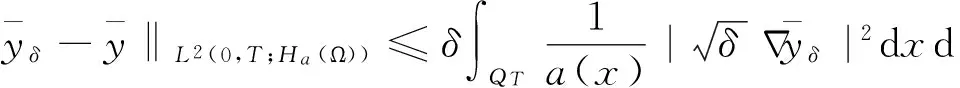
而
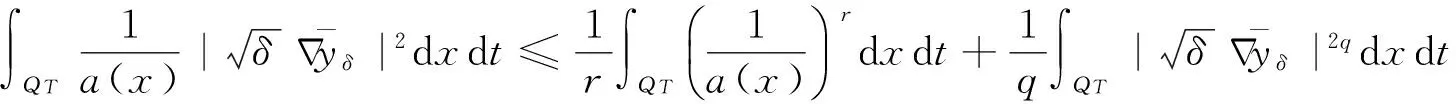
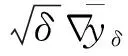
(7)
其中C2与δ无关.
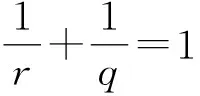
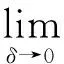
(8)

(9)
证明 对任意的η∈(0,1),存在Qη⊂QT,满足|Qη|=η|QT|.对任意的u(·)∈Uad定义
显然uη(·)∈Uad.
若yη(·)为问题(3)相应于uη(·)的解,则有
(10)
(10)与(5)式相减得
(11)
从而
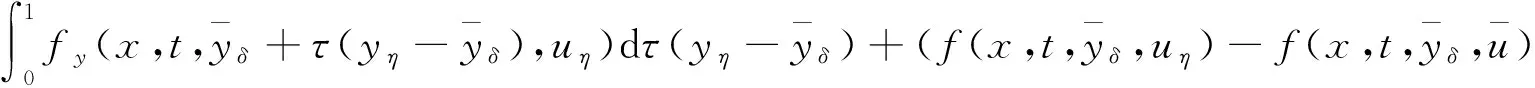
(12)
由抛物方程解的有界性估计理论有
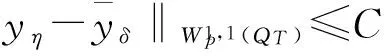
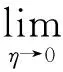
(13)
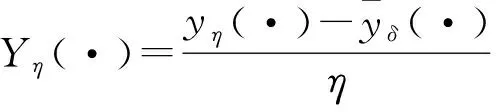
(14)
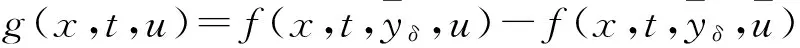
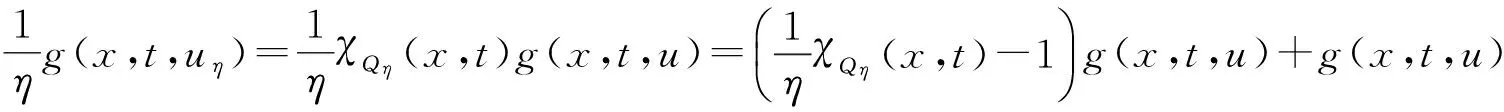
由Minkowski不等式有

而
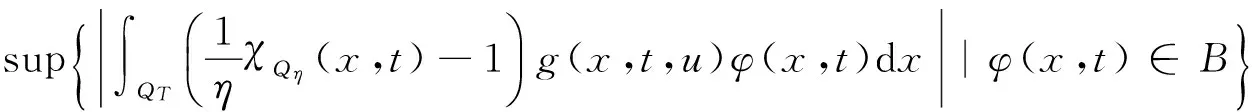
这里B为Lq(QT)中的单位球,故对任意ε>0,存在φ0(·)∈B,使得
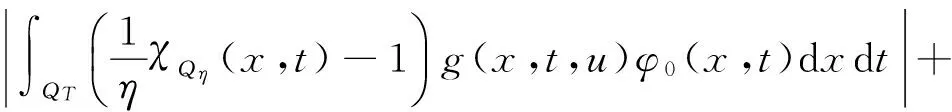
由文献[13],对任意ε>0,存在Qη⊂QT,满足|Qη|=η|QT|,有
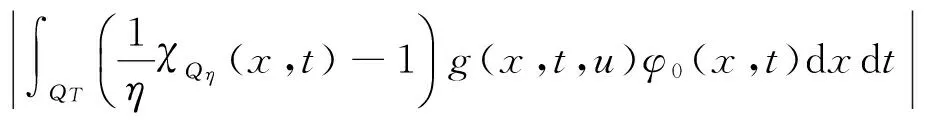
于是

(15)
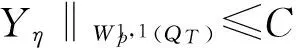
|Yη| (16) 下面证明当η→0时,Yη(·)→Yδ(·),其中Yδ(·)满足方程 (17) 将(14)与(17)式相减得 从而 于是 由(13)与(16)式得 且 令η→0,由(14)式即得(17)式为Yδ(·)满足的方程. 下面证明当δ→0时,Yδ(·)→Y(·),其中Y(·)满足方程(9). 在(17)式两端同乘Yδ,并在Ω上积分有 利用Young不等式和假设(P2)有 再由Gronwall不等式 (18) 从而存在Y(·)∈L2(QT)和Yδ(·)的一个子列,不妨记为其本身,使得 Yδ(·)→Y(·),δ→0, (19) (20) (21) (22) 由(22)式可得 (23) 令δ→0,利用(8),(19),(20)和(23)式,由(22)式可得 (24) 由(24)式即知Y(·)满足方程(9),亦称方程(9)为系统(1)的变分方程. 定理1的证明 首先证明广义解的存在性. 由文献[14]知问题(3)存在唯一的广义解yδ(·)∈L2(0,T;Ha(Ω))∩C(0,T;L2(Ω)).在(3)式两端同乘yδ并在Ω上积分有 再由Cauchy不等式,假设(P2)和Gronwall不等式有 从而 故存在y(·)∈L2(0,T;Ha(Ω))∩C(0,T;L2(Ω))及yδ(·)的一个子列,不妨记为其本身,满足: yδ(·)→y(·),δ→0; 类似引理2中证明可得 即y(·)∈L2(0,T;Ha(Ω))∩C(0,T;L2(Ω))是问题(1)的广义解. 再证广义解的唯一性. 再由假设(P2)可得 故 即 定理2的证明 对泛函作变分 令η→0,δ→0,利用假设(P3)上式化为 (25) 设变分方程(9)的对偶方程为方程(2),利用此对偶方程,(25)式可化为 再由变分方程(9)得 (26) 由(26)式可得 (27) 将(27)式除以ρ,再令ρ→0,由Lebesgue点定义得 根据H(x,t,v)的Lebesgue点集在QT中稠密有 [1] LI X J,YONG J M.Necessary conditions for optimal control of distributed parameter systems[J].SIAM J Control Optim,1991,29(4):895-908. [2] HU B,YONG J M.Pontryagin maximum principle for semilinear and quasilinear parabolic equation with pointwise state constraints[J].SIAM J Control Optim,1995,33(6):1857-1880. [3] FATTORINI H O.Optimal control problems with state constraints for semilinear distributed parameter systems[J].Optim Appl,1996,88(1):25-29. [4] CASAS E.Pontryagin’s principle for state-constrained boundary control problems of distributed parameter systems[J].SIAM J Control Optim,1997,35(4):1297-1327. [5] RAYMOND J P,ZIDANI H.Pontryagin’s principle for state-constrained control problems governed by parabolic equation with unbounded controls[J].SIAM J Control Optim,1998,36(6):1853-1879. [6] 高夯.半线性抛物方程支配系统的最优性条件[J].数学学报,1999,42(4):705-714. [7] BONNANS J F,JAISSON P.Optimal control of a parabolic equation with time dependent state constraints[J].SIAM J Control Optim,2010,48(7):4550-4571. [8] 赵坚,高夯.抛物系统的最优初值控制问题[J].东北师大学报(自然科学版),2015,47(3):1-4. [9] LENHART S M,YONG J M.Optimal control for degenerate parabolic elliptic equation with logistic growth[J].Nolinear Anal,1995,25(7):681-698. [10] WANG C.Approximate controllability of a class of degenerate systems[J].Appl Math Comput,2008,203:447-456. [11] 伍卓群,尹景学,王春朋.椭圆与抛物型方程引论[M].北京:科学出版社,2003:208-216. [12] ADAMS R A,FOURNIER J J F.Sobolev space[M].2nd ed.Singapore:Elsevier Pte Ltd,2003:79-101. [13] LI X J,YONG J M.Optimal control theory for infinite dimensional systems[M].Boston:Birkhauser,1995:163-172. [14] LADYZHENSKAVA O A,URALTSEVA A N.Linear and quasilinear parabolic equation[M].New York:Academic Press,1968:258-272. (责任编辑:李亚军) Optimal control problems for system governed by a class of degenerate semilinear parabolic equation ZHANG Jing1,GAO Hang2 (1.School of Science,Qiqihar University,Qiqihar 161006,China; 2.School of Mathematics and Statistics,Northeast Normal University,Changchun 130024,China) Optimal control problems for distributed parameter system governed by a class of degenerate semilinear parabolic equation are considered.When the measure of degenerate-points is zero,Pontryagin maximum principle for optimal control of the distributed parameter system is obtained by using regularization method and variational thought. degenerate semilinear parabolic equation;optimal control;regularization method;variational thought;Pontryagin maximum principle 1000-1832(2017)01-0001-08 10.16163/j.cnki.22-1123/n.2017.01.001 2015-08-09 国家自然科学基金资助项目(11071036);黑龙江省自然科学基金资助项目(QC2016008);黑龙江省教育厅科学技术研究项目(12541891). 张敬(1969—),女,硕士,教授,主要从事控制论与偏微分方程研究;高夯(1956—),男,博士,教授,博士研究生导师,主要从事控制论与偏微分方程研究. O 232 [学科代码] 120·30 A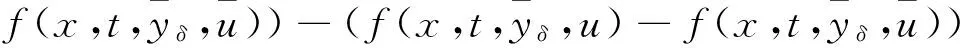
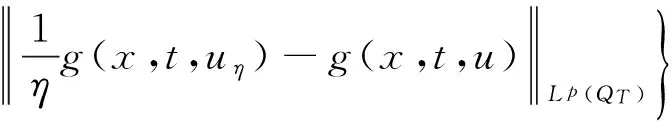

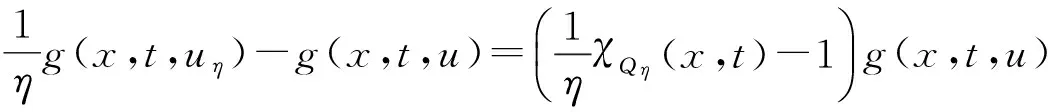
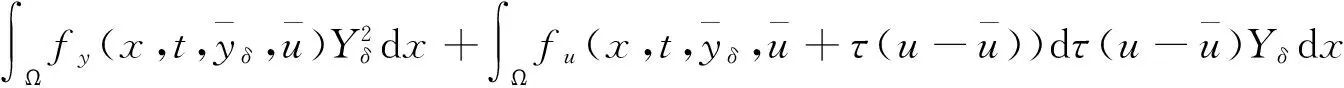
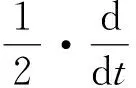
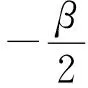
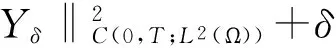
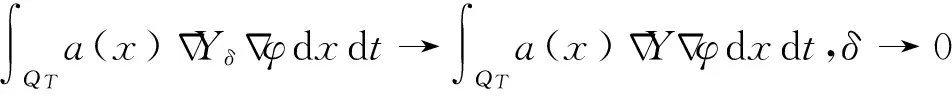
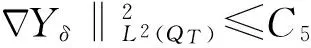

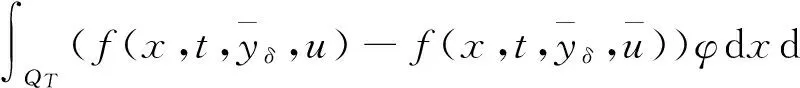


3 主要定理的证明