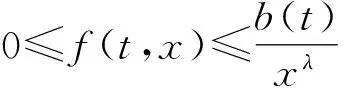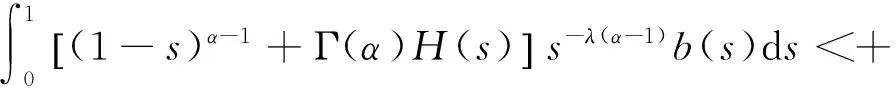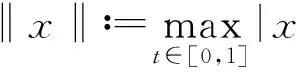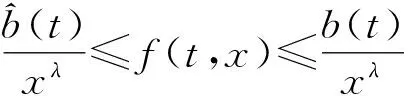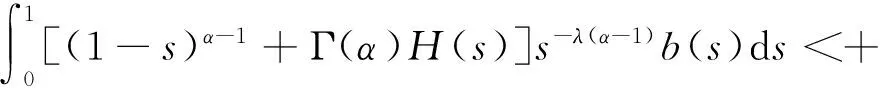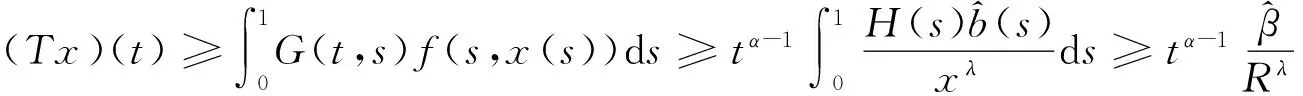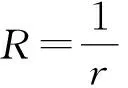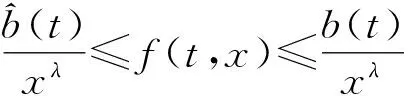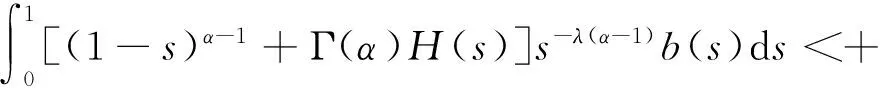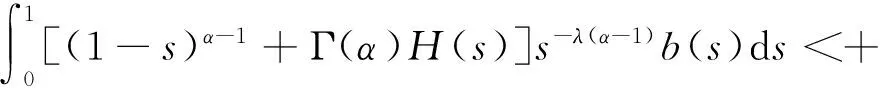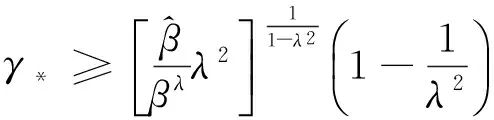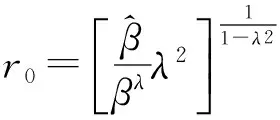Schauder不动点定理在分数阶m-点边值问题中的应用

王丽颖，许晓婕

(1.白城师范学院数学与统计学院，吉林 白城 137000；2.中国石油大学理学院，山东 青岛 266555)

Schauder不动点定理在分数阶m-点边值问题中的应用

王丽颖1，许晓婕2

(1.白城师范学院数学与统计学院，吉林 白城 137000；2.中国石油大学理学院，山东 青岛 266555)

用Schauder不动点定理研究了分数阶m-点边值问题

正解；Schauder不动点定理；m-点边值问题；分数阶微分方程

最近，分数阶微分方程引起了人们的极大关注，这不仅是其自身理论发展的需求，同时也是其广泛应用的必然结果.除了在数学各方面的应用外，分数阶微分方程还在流体力学、流变学、黏弹性力学、分数控制系统与分数控制器等方面，特别是与分形维数有关的物理与工程方面有着广泛的应用.[1-2]最近，有些学者应用非线性技巧，如Leray-Schauder定理等研究分数阶微分方程Dirichlet型等边值问题.[3-7]关于Schauder不动点定理在微分方程及分数阶微分方程上的应用已有一些结果[8-10]，但是Schauder不动点定理在m-点边值问题中的应用目前还未见相关研究.本文考虑m-点边值问题

(1)

1 预备知识

引理1[7]假设u∈C(0，1)∩L(0，1)，且其α>0阶导数属于C(0，1)∩L(0，1).则

其中N是大于或等于α的最小整数.

引理2 给定y∈C(0，1)，方程

G(t，s)=G1(t，s)+G2(t，s).

G2(t，s)=H(s)tα-1，

引理2.2的证明可由引理1得到，此处略去.

定理1 由上式定义的格林函数G(t，s)具有如下性质：

(α-1)tα-1s(1-s)α-1(1-t)≤Γ(α)G1(t，s)≤tα-1(1-s)α-1，t，s∈[0，1]；

(2)

(3)

证明 首先考虑Γ(α)G1(t，s).当0≤s

(α-1)tα-1(1-s)α-1s(1-t)≥0.

(4)

易证当0≤t

Γ(α)G1(t，s)≥(α-1)s(1-t)[t(1-s)]α-1≥0，

(5)

从而(2)式证毕.(3)式只需证明H(s)≥0.事实上，

(6)

2 主要结果

考虑m-点边值问题

如果γ*>0，则方程(1)至少存在一个正解.

Ω={x∈C[0，1]|t∈[0，1]，tα-1r≤x(t)≤tα-1R}，

其中R>r>0是待定的正常数.

定义映射T:Ω→E，

则由Schauder不动点定理知问题(1)解的存在性等价于x=Tx不动点的存在性.下面只需证T(Ω)⊂Ω.

事实上，固定r∶=γ*，由假设知r>0，a.e.t∈(0，1).∀x∈Ω，由假设可知

下面考虑γ*=0的情况.

其中

如果γ*=0，则方程(1)至少存在一个正解.

下面考虑γ*<0<γ*的情况.

其中

如果γ*<0<γ*，且

(7)

证明 使用和上面定理相同的记号和方法，为证T(Ω)⊂Ω，只要找到0

(8)

(9)

从而

令F′(m)=0，则

(10)

(11)

下面考虑γ*≤0的情况.

如果γ*≤0，且

(12)

则方程(1)至少存在一个正解.

证明 使用与上述定理相同的记号和方法，为证T(Ω)⊂Ω，只要找到0

(13)

[1] NONNENMACHER T F，METZLER R.On the Riemann-Liouville fractional calculus and some recent applications[J].Fractals，1995，3：557-566.

[2] TATOM F B.The relationship between fractional calculus and fractals[J].Fractals，1995，3：217-229.

[3] BAI ZHAN BING，LU HAI SHEN.Positive solutions for boundary value problem of nonlinear fractional differential equation[J].J Math Anal Appl，2005，311：495-505.

[4] JIANG DA QING，YUAN CHENG JUN.The positive properties of Green’s function for Dirichlet-type boundary value problems of nonlinear fractional differential equations and its application[J].Nonlinear Analysis Series A：Theory，Methods and Applications，2010，72：710-719.

[5] RAVI P AGARWAL，DONAL O’REGAN，SVATOSLAV STANEK.Positive solutions for Dirichlet problems of singular nonlinear fractional differential equations[J].J Math Anal Appl，2010，371：57-68.

[6] 胡卫敏，伊磊，陈维.一类分数阶微分方程三点边值问题的多重正解[J].东北师大学报(自然科学版)，2011，43(2):16-22.

[7] 张丽娟，胡卫敏.一类Dirichlet型非线性分数阶微分方程边值问题的正解[J].东北师大学报(自然科学版)，2012，44(2):31-35.

[8] 王丽颖，许晓婕.Schauder不动点定理在共轭边值问题中的应用[J].吉林大学学报(理学版)，2010，48(4)：551-556.

[9] 王丽颖，许晓婕.Schauder不动点定理在分数阶三点边值问题中的应用[J].吉林大学学报(理学版)，2012，50(2)：195-200.

[10] 王丽颖，许晓婕.Schauder不动点定理在分数阶三点边值问题中应用的新结果[J].吉林大学学报(理学版)，2013，51(2)：173-178.

(责任编辑：李亚军)

Applications of Schauder’s fixed point theorem to point boundary value problem of fractional differential equations

WANG Li-ying1，XU Xiao-jie2

(1.School of Mathematics and Statistics，Baicheng Normal College，Baicheng 137000，China； 2.College of Science，China University of Petroleum，Qingdao 266555，China)

The existence of positive solutions form-point boundary value problem of fractional differential equations is considerede.TheproofsrelyonSchauder’sfixedpointtheoremonfourcasesγ*>0，γ*=0，γ*<0<γ*andγ*≤0.

positive solutions； Schauder’s fixed point theorem；m-point boundary value problem； fractional differential equations

1000-1832(2017)01-0020-05

10.16163/j.cnki.22-1123/n.2017.01.004

2015-06-07

国家自然科学基金资助项目(11571207)；中央高校基金资助项目(16CX02015A).

王丽颖(1973—)，女，硕士，教授，主要从事微分方程研究.

O 175.08 [学科代码] 110·44

A