一道高考题的解答、推广和溯源

☉湖北省华中师范大学第一附属中学 骆冰翘

一道高考题的解答、推广和溯源

☉湖北省华中师范大学第一附属中学 骆冰翘

细品2015年湖北高考数学理科卷第14题：平而不俗，内涵丰富．笔者在老师的指导下进行了一次极具收获性的探究，整理出来，以引发思索．

试题如下：如图1，圆C与x轴相切于点T（1，0），与y轴正半轴交于两点A，B（B在A的上方），且|AB|=2．

（1）圆C的标准方程为_________．

（2）过点A任作一条直线与圆O：x2+y2=1相交于M，N两点，

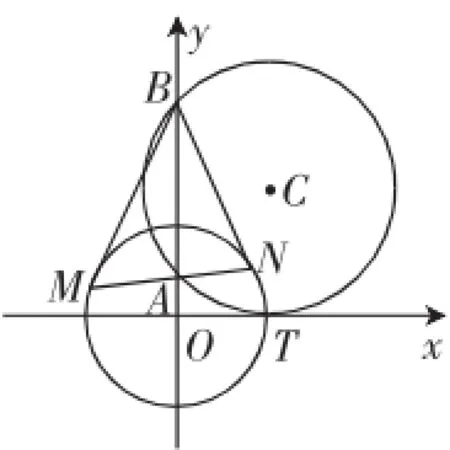
图1

其中正确结论的序号是________（写出所有正确结论的序号）．

一、问题的解答

解析：（1）不妨设圆C的标准方程为：（x-1）2+（y-r）2= r2（r＞0）．

由|AB|=2知，12+12=r2=2，则C：（x-1）2+

毋庸置疑，本题第（2）问是难点，此问对科学素养有一定的要求，很多同学难以揣摩出命题者的意图，只能蛮干甚至徒劳．对于多结论的正误判断、验证类问题，盲目逐一检验是不可取的，善于比对、分析结论间关系才是研究的第一步．之前在“抛物线的焦点弦的众多衍生性质、结论的证明”学习中已然有了经验，为何在此却全无分寸呢？只因科学的研究方法和手段还没形成“自主意识”．

我们在做题过程中，很容易集中于一个一个地去判定结论是否正确，对于①，容易想到等价证明OB是∠MBN的角平分线，而且会判断M、A、N三点共线是证明该结论必不可少的条件．于是对于①，同学有如下做法：

故OB是∠MBN的角平分线．

这样历经千辛万苦终于证明了①，但是无论①的证明过程，还是①这个结论本身，对后面②③的判断都没有本质上的帮助．因为时间的关系，我们可能只能选择取特殊情况，比如M、N关于y轴对称时，对②③的正误进行一个不保险的判断．实际上，如果能认真比较①②③的区别，不难推测此题可能是要证明为定值．于是，就有了下面的思路，看似平淡无奇，实则效果很好．

故①②③皆正确．

（2）方法2：如图2，过A点作OB的垂线交圆O于点C，D，连接OD．

图2

故OD⊥BD．

在△ODB中，由射影定理知，AD2=AB·AO，①

又AD·AC=AN·AM，即AD2=AN·AM，②

故AB·AO=AN·AM，所以O，N，B，M四点共圆，

则∠AMO=∠ABN，易得△OMA～△NBA，

二、问题的推广

推广是数学研究的重要手段之一，数学知识的完备、数学本身的发展在很大程度上都依赖于推广．通过该问题我们发现在圆的背景下对给定的两定点A，B总有坐标轴平分该张角，那我们自然会思考A，B两点坐标会满足什么一般性规律呢？

结论如图1，已知圆O：x2+y2=r2（r＞0），及点A（0，m），B（0，n）．过点A任作直线交圆O于M，N两点，AB平分∠MBN的充要条件是mn=r2．

为节约篇幅，该结论和以下三个推广的证明省略，感兴趣的读者可自行证明．

倘若在圆中有此结论，那在椭圆、双曲线与抛物线中呢？因而有了以下三个推广．

推广3如图5，已知抛物线C：x2=2py（p＞0），及点A（0，m），B（0，n）．过点A任作直线交抛物线C于M，N两点，AB平分∠MBN的充要条件是m+n=0．

图3

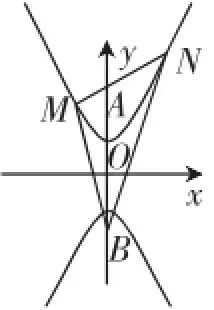
图4

图5

如2015年四川理科数学卷第20题，正是推广1的应用：

图6

（1）求椭圆E的方程．

（2）在平面直角坐标系xOy中，是否存在与点P不同的定点Q，使得恒成立？若存在，求出点Q的坐标；若不存在，请说明理由．

又如2015年全国卷Ⅰ理科数学第20题，是推广3的应用：

（1）当k=0时，分别求C在点M和N处的切线方程；

（2）y轴上是否存在点P，使得当k变动时，总有∠OPM=∠OPN？说明理由．

三、问题的溯源

阿氏圆的定义可用来求解圆的方程，还可以在证明题中运用其来通过圆上一个点与两定点距离比例从而得知另外一个圆上的点与两定点距离的比，还常常作为角度比值、共线向量的模长比值等问题的“题根”熠熠生辉．

如2013年江苏省高考数学理科卷第17题：

如图7，在平面直角坐标系xOy中，点A（0，3），直线l：y=2x-4．设圆C的半径为1，圆心在l上．若圆C上存在点M，使MA=2MO，求圆心C的横坐标a的取值范围．

又如2014年湖北省高考数学文科卷第17题：

已知圆O：x2+y2=1和点A（-2，0），若定点B（b，0）（b≠-2）和常数λ满足：对圆O上任意一点M，都有|MB|=λ|MA|，则（1）b=________；（2）λ= __________．

这里我们得到的经验就是：研究问题要注重本身，凸显关联，强调实质．解法上力争突破常规，有所创新；推广上尽力辐射出更多知识间联系，以打通知识经脉；源头上紧抓问题的本质属性，加深对知识的理解，有助于知识网络的重构与优化．正如傅种孙先生所说：“数学学习，一是知其然，二是知其所以然；三是知何由以知其所以然．”

图7