小议二次函数综合性问题突破视角

☉江苏省常熟市浒浦高级中学 夏朴

小议二次函数综合性问题突破视角

☉江苏省常熟市浒浦高级中学 夏朴

众所周知，高中数学函数问题最经典的模型是以二次函数为背景设计的，二次函数既因为在生活生产实际中有着重要体现，也是中学生能够解决的主要模型．通过二次函数可以研究函数的三要素、单调性、最值以及在问题解决过程中涉及的重要思想方法等．可以这么说，二次函数相关的综合性问题一直是学生学习的难点．

从考试要求来看，“考试大纲”明确提出了理解二次函数的定义，掌握其图像和性质，以及理解和运用二次函数、一元二次方程、一元二次不等式之间的关系去解决相关问题，在问题解决过程中能够运用思想方法将问题转化为二次函数求解．从大纲要求来看，很明显提出了二次函数学习的三个层次，其一是掌握基本知识和基本性质，这是大部分学生普遍掌握的；其二是能运用整合性的知识联系解决相关问题，这就选拔出了能力较强的学生；最后是能运用思想方法将综合性问题通过二次函数模型求解，体现了选拔最优秀学生的意图．近年来，二次函数以综合性问题呈现在试卷中，以函数、不等式、方程的相互等价转换成为命题的常规形态，以导数的介入、解析几何中的渗透成为有效的结合点．从难度来说，二次函数的深入挖掘成为区分学生能力的重要考核手段，成为教师教学关注的重点．下文从综合性问题举例来说明，教学中应该选择的突破视角．

一、图形的视角

“小题小做”一直是高考重要的命题原则，也就是说要利用更为直观、特殊的方式去解决小题．笔者认为，对于二次函数综合性小题的解决，多利用图形化的视角尝试是首要的选择，看一个例题：

分析：借助二次函数的图像，我们不难发现：值域为定值，因此其定义域可以在一定范围内变化，这种变换通过图形的视角显露无遗（如图1），借助图形的对称性可以得到两者之间的关系如图1所示．

解析：令y=3，即x2-2x=3，解得x1= 3，x2=-1．又x=1时，y=-1，因此当a=-1时，1≤b≤3都可以，即线段AB；当b=3时，-1≤a≤1都可以，即线段AD．

点评：小题小做最常用的手段是图形化视角、特殊化视角，拥有这样的思维状态对于考试有极大的帮助．本题较为合理地借助图形化视角，将图形中自变量的变换显示出来，厘清变量间的对应关系．本题还可以对相关问题进行变换：如将其变式为求|a-b|的最大值或者最小值等等．

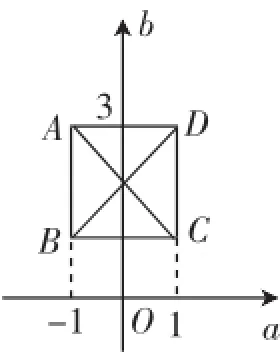
图1

二、转换主元的视角

二次函数含参变量问题是考查的难点之一，随着参数的增多，学生对于问题的处理往往陷入混沌．在思考问题过程中，我们可以转换研究主要元素的视角，让问题呈现一种清晰的突破口．

问题2函数f（x）是定义在［-1，1］上的奇函数，且f（1）=1，若a，b∈［-1，1］，且a+b≠0时，恒有

（1）判断并证明f（x）在［-1，1］上的单调性；

（2）若f（x）≤m2-2am+1对所有a∈［-1，1］恒成立，求m的取值范围．

作为一名思想政治教育者,首先要克服首因效应和近因效应所造成的认知偏见对教育者的影响，不能只凭第一印象或最新印象评价和判断人，也不能轻信任何一种关于某人的信息，而应当用全面的、辩证的观点看问题以及了解他人。教育者还可以充分利用首因效应和近因效应的积极作用,在教育内容的选择上利用二者提高教学效果。在与人相处时注意自己的仪容仪表、谈吐等，给人留下良好的第一印象，作为教育者来说，开学第一课至关重要，准备好开学第一课，给学生留下良好的印象。但更重要的是要有意识地引导教育对象用全面的观点看问题。

分析：这是一个多元参量的典型问题．对于第（2）小问，我们不难发现学生难以清晰地辨解多个参量，不少学生无从下手．从问题的剖析来看，应该是这样严密的完整表述：“若f（x）≤m2-2am+1对任意的x∈［-1，1］，a∈［-1，1］都恒成立，求m的取值范围．”因此首先研究哪个变量、进而研究哪个变量非常清晰，我们层层递进来分析．由第（1）小问单调性可知，从变量x入手，即研究m2-2am+1≥f（x）max，这里可以说不费吹灰之力；在得到m2-2am≥0时思考哪个元素已经告知？进一步研究哪个元素的问题？显然变量a的范围已经告知，进一步研究变量m的取值范围，因此转换主元的视角跃然纸上，从而多个变量的问题也层层剥离，清晰求得．

解析：（1）略．

（2）因为f（x）≤m2-2am+1对所有x∈［-1，1］，a∈［-1，1］恒成立，即m2-2am+1≥f（x）max．

因为f（x）max=f（1）=1，所以m2-2am+1≥1，所以m2-2am≥0，即g（a）=-2am+m2≥0在［-1，1］上恒成立．

点评：转换主要元素研究的视角是常见的二次函数综合性问题选择方法，通过元素主次位置的确定，将问题转换为较为容易的函数模型，上述问题经过转换主元成为一次函数的研究，使得问题的解决变得容易很多．对于学生而言，转换主元的视角是思考多元变量问题的恰当手段，教学经验也告诉我们学生对于这种转换尚不能合理接受，不少学生仍旧在二次函数的分类讨论上大做文章，这种做法不可取，加强学生解题视角的引导成为关键．

三、变量分离的视角

对于二次函数综合性问题来说，为了避免大量的分类讨论，还可以从变量分离的视角入手思考问题．变量分离是综合性问题的重要方法，即将研究的变量和参量进行合理的分离，这种分离最好是基于不用分类讨论进行．变量分离的视角是很多问题的重要选择方法，诸如恒成立问题、存在性问题、有解性问题等等．

（1）求m，n的值；

（2）当x∈［1，+∞）时，判断函数f（x）的单调性并证明；

分析：（1）略；（2）利用定义法或导数法加以证明；（3）中限制了字母参数的范围的“三个二次”问题可以转换变量来加以化解，而本题限制了自变量的范围，一个比较简洁的办法就是分离变量，将含有自变量的放在一起，构造一个新的函数然后再研究新函数的最值．

解：（1）（2）略．

（3）由题可知，2x2-2x+1＞2a（x-1）在x∈（2，4）上恒成

点评：为什么会想到利用参变分离的视角？这是教学需要向学生阐述的关键．考虑到变量x∈（2，4），显然在分离过程中不需要对其进行讨论，自然分离成为了解决问题的首选方式．此类问题单刀直入，紧抓最终的目标，先简化等式或不等式的一边，然后利用函数的性质研究新函数的最值．此法也可以推广到次数更高的问题．学生面对这类题型的最大问题：一方面在较复杂的问题情境中很难将目标字母理清楚，另一方面对于除过去的式子2（x-1）的分析，如果x∈（0，4），使得式子2（x-1）有正有负也有0，就要进行分类讨论，更要关注不等号的方向．学生常见的错误就是对不等式的两边分开讨论，但问题是两边不在同一处取得最值．当然此题也可以用分类讨论方法解决．

四、凹凸性的视角

函数凹凸性是高等数学必备的学识之一，但在中学数学中对于凹凸性的认识并不深刻，也没有特别的相关概念介绍．在导数相关知识中，对于函数研究过程中能利用凹凸性视角，大大简化了问题的求解过程．

问题4已知函数f（x）=ax2+bx+c（a≠0）的图像过（-1，0）点，则存在常数a，b，c，使不等式对一切实数恒成立．

图2

点评：本题恒成立的求解另辟蹊径，从两边夹f（1）= 1入手，思考恒成立后续问题的处理，通过思考即可发现只要找到直线与抛物线、抛物线与抛物线相切位置即可知道，其余点处恒成立．思考抛物线凹凸性可知，寻找切点必定出于两边夹的特殊值位置，即f（1）=1处，这说明函数凹凸性的理解大大简化了一般学生利用判别式法求解的过程，体现出了思维的含量、突破的新视角，可见对于上凸或下凸函数等有深刻的认知、提前的预判量，大大提高了问题解决的可能性，是引导优秀学生思维的新视角．

总之，二次函数综合性问题的处理是一个渐学渐长的过程．从本文所举的四个案例来看，对小题和多元变量的处理，灵活掌握知识、合理选择使用是综合二次函数问题的常见方法和技能，是突破的常见视角．上述问题也能从其他视角入手，有兴趣的读者也可以一试，对比文中所选视角，可能会有意想不到的收获．

1.柴贤亭.函数教学中的思维启发设计［J］.教学与管理，2013（8）.

2.郑毓信.解题教学理论在二次函数中的实践［J］.中学数学月刊，2015（1）.