例谈高考中绝对值问题的解题策略

☉江苏省泗洪中学 陈亚娟

例谈高考中绝对值问题的解题策略

☉江苏省泗洪中学 陈亚娟

含绝对值的问题呈现出命题立意新颖、思维方式抽象、解题方法灵活、综合性强等特点，是近年来高考中一颗璀璨的“明珠”，常常出现在高考的压轴题中．解决此类问题的办法一般是：数形结合或依据参数进行分类讨论等，下面笔者结合自己的教学实践谈一些想法．

一、常见含绝对值函数类型

常见的绝对值函数主要包括y=|f（x）|和y=f（|x|）两种类型，由于自变量x的取值被分成若干不同的区间，绝对值函数在不同的区间有不同的表达式：

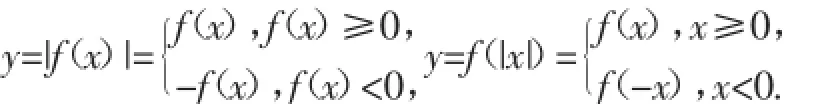
其图像作法可依不同区间分别来作：y=|f（x）|的图像可以由y=f（x）的图像在x轴上方不变，x轴下方的沿x轴向上翻折后所得；y=f（|x|）的图像可以由y=f（x）的图像在y轴右方不变，并将y轴右方的图象沿y轴向左翻折后所得．一般含绝对值的函数问题均可由以上两种基本绝对值函数组合或变换得到．

二、解题策略

（一）数形结合

华罗庚教授说：“数缺形时少直观，形缺数时难入微，数形结合千般好，隔离分家万事休．”就是说，“以形助数，以数解形”，能使复杂问题简单化，从形的直观和数的严谨两方面思考问题，能拓宽解题思路，是数学的规律性与灵活性的有机结合，利用这些特性作出函数图像，解决数学问题．

例1已知函数f（x）=|x2+3x|，x∈R．若方程f（x）-a|x-1|=0恰有4个互异的实数根，则实数a的取值范围为__________．

解法1：显然a＞0．

（i）当y=-a（x-1）与y=-x2-3x相切时，如图1，a=1，此时f（x）-a|x-1|=0恰有3个互异的实数根．

图1

图2

（ii）当直线y=a（x-1）与函数y=x2+3x相切时，如图2，a=9，此时f（x）-a|x-1|=0恰有2个互异的实数根．

结合图像可知，0＜a＜1或a＞9．

结合图3可得0＜a＜1或a＞9．

点评：利用数形结合求方程解（或函数的零点）应注意三点：

（1）讨论方程的解（或函数的零点）可构造两个函数，使问题转化为讨论两曲线的交点问题，但用此法讨论方程的解一定要注意图像的准确性、全面性，否则会得到错解或漏解．

（2）正确作出两个函数的图像是解决此类问题的关键，数形结合应以“快”和“准”为原则，不要刻意去数形结合．

（3）注意挖掘隐含条件，结合图像的临界位置，准确地界定图形的范围，图形的范围决定参数的取值范围．

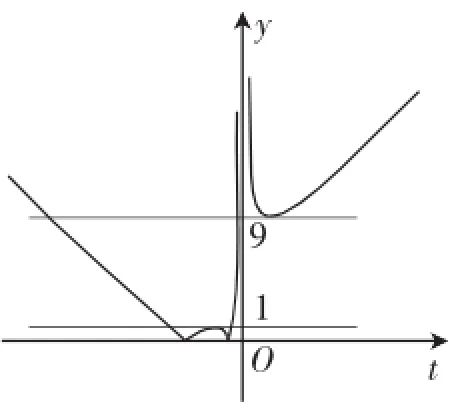
图3

（二）分类讨论，逐步转化

常见的绝对值函数问题，以考查思维能力为核心，强调探究性、综合性、应用性和创新意识．因此，教师要创新情境，引导学生在陌生情境中自我探索，独立地思考分析问题，揭示其中的联系和奥秘，在问题变化不定时，会用分类讨论等数学思想将数学对象分为不同种类，然后对划分的每一类分别进行研究或求解，从而达到“化难为易，化整为零，各个击破”的目的．

例2已知函数f（x）=x3+3|x-a|（a∈R）．

（1）若f（x）在［-1，1］上的最大值和最小值分别记为M（a），m（a），求M（a）-m（a）；

（2）设b∈R，若［f（x）+b］2≤4对x∈［-1，1］恒成立，求3a+b的取值范围．

由于-1≤x≤1，所以：

（i）当a≤-1时，有x≥a，故f（x）=x3+3x-3a，

此时f（x）在（-1，1）上是增函数，因此M（a）=f（1）=4-3a，m（a）=f（-1）=-4-3a，M（a）-m（a）=4-3a-（-4-3a）=8．

（ii）当-1＜a＜1时，

若x∈（a，1），f（x）=x3+3x-3a，在（a，1）上是增函数，

若x∈（-1，a），f（x）=x3-3x+3a，在（-1，a）上是减函数，

所以M（a）=max｛f（-1），f（1）｝，m（a）=f（a）=a3，

由于f（1）-f（-1）=-6a+2，

（iii）当a≥1时，有x＜a，故f（x）=x3-3x+3a，此时f（x）在（-1，1）上是减函数，因此M（a）=f（-1）=2+3a，m（a）=f（1）=-2+3a，故M（a）-m（a）=2+3a-（-2+3a）=4．

因为［f（x）+b］2≤4，对x∈［-1，1］恒成立，

即-2≤h（x）≤2对x∈［-1，1］恒成立，所以由（1）知，

（i）当a≤-1时，有x≥a，h（x）=x3+3x-3a+b在［-1，1］上是增函数，h（x）在［-1，1］上的最大值是h（1）=4-3a+b，最小值是h（-1）=-4-3a+b，则-4-3a+b≥-2，且4-3a+b≤2，即-3a+b≥2，-3a+b≤-2矛盾．

＜a＜1时，h（x）在［-1，1］上的最大值是h（-1）=3a+b+2，最小值是h（a）=a3+b，所以a3+b≥-2，3a+ b+2≤2，解得

（iv）当a≥1时，有x＜a，h（x）=x3-3x+3a+b在［-1，1］上是减函数，h（x）在［-1，1］上的最大值是h（-1）=3a+b+2，最小值是h（1）=-2+3a+b，所以3a+b+2≤2，-2+3a+b≥-2，解得3a+b=0．

综上，3a+b的取值范围-2≤3a+b≤0．

点评：本题主要考查函数最大（最小）值的概念、利用导数研究函数的单调性等基础知识，同时考查推理论证、分类讨论、分析问题和解决问题等综合解题能力．分类原则：（1）所讨论的全域要确定，分类要“既不重复，也不遗漏”；（2）在同一次讨论中只能按所确定的一个标准进行；（3）对多级讨论，应逐级进行，不能越级；（4）总结概括，得出结论．

（三）反客为主，运用反解系数解决

一类定区间上二次函数含绝对值的最值问题频频出现在模考、高考、竞赛试题中，许多学生会无从下手．有时将所求的参数反解出来，揭示这类最值问题的背景及内涵，并发现其中蕴涵的规律和方法，就可以达到触类旁通、举一反三的效果，真正让学生从题海中解放出来．

例3已知函数f（x）=ax3+bx2+cx+d（a≠0），当0≤x≤1时，|f′（x）|≤1，试求a的最大值．

解：由f′（x）=3ax2+2bx+c，得

点评：问题中f′（x）=3ax2+2bx+c是二次函数，求a的最大值是单个系数的最值处理方法，解题时用区间［0，1］上的两个端点和中点函数值来反解表示系数a，同时利用绝对值函数性质|a±b|≤|a|+|b|进行求解，就获得了解决．

（四）活用圆锥曲线的定义

类似椭圆类不等式|x-c|+|x+c|≤2a（a＞c）的解为-a≤x≤a或|x-c|+|x+c|≥2a（a＞c）的解为x≤-a或x≥a；类似双曲线类不等式||x-c|-|x+c||≤2a（a＜c）的解为x≤-a或x≥a或||x-c|-|x+c||≥2a（a＜c）的解为-a≤x≤a．常常可以利用圆锥曲线定义解一类绝对值不等式．

例4不等式|x-1|+|x+2|≥5的解集为________．

此题为椭圆类不等式．问题关键：用椭圆的定义求出它的“中心”、“顶点”即可．

解：根据椭圆类不等式2a=5，2c=1-（-2）=3，“中心”

故由圆锥曲线定义易得不等式|x-1|+|x+2|≥5的解集为

（五）利用绝对值三角不等式

绝对值三角不等式在解决一些含绝对值问题中起着非常重要的作用．

例5求函数y=|2x-1|+|x-1|+|x-2|的最小值．

三、结束语

含绝对值的函数题型综合性很强，它常常综合二次（或三次）函数图像与最值、函数的单调性、绝对值不等式的性质、线性规划等知识的综合考查，同时考查数形结合思想、分类讨论思想、转化与化归思想等数学思想以及运算求解能力．从以上的解题策略来看，我们主要采用绝对值不等式的性质即纯代数方法来解题和结合图像的数形结合的思想来解．借助于分类讨论，将问题条理化、系统化、清晰化，然后运用函数、方程及不等式的思想，灵活转化，解决运动和变化中出现的问题，给学生提供思考的空间，使他们的聪明才智在解题中得到充分的展示，进而体现了高考数学“考素质，考能力”的要求．因此，在复习时，教师要特别强调“形”与“数”的灵活转化及分类讨论的思想方法，它不仅是我们解题的一种思想方法，更是我们进一步学习、研究数学的有力武器．