三点共线向量式藏在深闺人未识巧用解题有优势

☉西南大学附属重庆市梁平实验中学 蒋明建

三点共线向量式藏在深闺人未识巧用解题有优势

☉西南大学附属重庆市梁平实验中学 蒋明建

一、三点共线向量式定理的背景

人教A版普通高中课程标准实验教科书《数学·4》（必修）第二章向量中有这样的结论（第99页例8）：如图1所示，设点P是线段P1P2上的一点，P1，P2的坐标分别是（x1，y1），（x2，y2）.

图1

（1）当点P是线段P1P2的中点时，则O →P=

（2）当点P是线段P1P2的一个三等分点（不妨取

二、三点共线向量式定理及证明

由于这一结论隐藏在普通例题之中，不深入挖掘难以发现，一般很少将其视为定理直接用于解题，真让人有“未展芳容缘何来，藏在深闺人未识”之感.事实上，注意挖掘利用三点共线向量式这一定理（以下简称“定理”）解决有关问题，往往能收到事半功倍的效果，令人拍案叫好！本文通过运用“定理”对一些典型问题的求解，展现了“定理”在解题运用中的美妙与神韵.

三、定理的巧妙运用

（一）在三点共线判断问题中的巧妙运用

三点共线问题，如果条件是向量形式给出的，就可根据三点共线向量式结论直接判断.

例1已知A，B，C是直线l上的不同三点，点O不在l上，则关于x的方程的解集为_______.

已知A，B，C三点共线，根据“定理”知，（1-2x2）+（-x） =1，解得x=0

评注：题目已知条件明显具备三点共线特征，直接运用“定理”求解，一步到位，简洁明快．

（二）在用基向量表示其他向量问题中的巧妙运用

用基向量表示其他向量是平面向量的常见问题，利用“定理”能使问题求解变得十分简便．

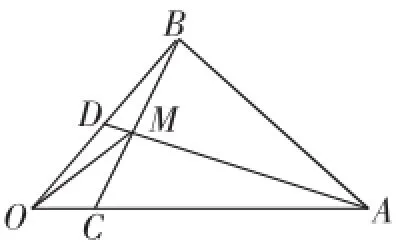
图2

解：如图2，因为A，M，D三点共线，由“定理”知，存在实数λ，使得

（三）在求值问题中的巧妙运用

1．求三角形面积

例3（2004年全国高中数学联赛题改编）已知P是△ABC内一点，且，△PBC的面积是2015，则△PAB的面积是_______．

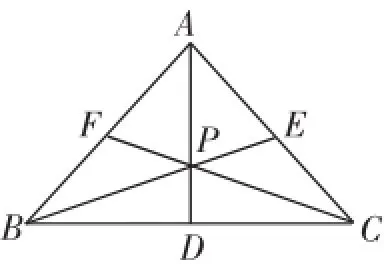
图3

(3)所检桥梁部分支座挡块有开裂、破损、与梁体间隙过小及露筋现象，支座挡块与盖梁连接处存在较多的混凝土破损、开裂现象。

同理，延长BP，CP分别交AC，AB边于E，F（图3），算xy≠0），且x+2y=1，求cos∠BAC的值．

2．求三角形的角

例4已知O为△ABC的外心，AB=2，AC=3，若

3．求最值

S′（α）=-sinα-sin2α+cos2α=-2sin2α-sinα+1．

4．求比值

例6设M，N分别是正六边形ABCDEF的对角线AC，CE的内分点，且若B，M，N三点共线，求λ的值．

解：如图4，延长EA，CB交于点P，不妨设正六边形的边长为1，易知△ECP

图4

评注：以上几个例题，充分运用三点共线向量式定理求解，思维起点低，思路直接，有效避免了向量回路法运算的烦琐，使问题求解简便易行．

（四）在求数列问题中的巧妙运用

例7（2015重庆一中高考模拟试题第9题）如图5，已知点D为△ABC的BC边上一点En（n∈N+）为边AC上的一列点，满，其中实数列｛an｝中an＞0， a1=1，则数列｛an｝的通项公式为（）．

图5

A．2·3n-1-1B．2n-1 C．3n-2D．3·2n-1-2

因为A，C，En（n∈N+）三点共线，所以，根据“定理”，，即an+1+1=3an+3，则an+1+1= 3（an+1），数列｛an+1｝是以2为首项，3为公比的等比数列，求得an=2·3n-1-1，选A．

评注：注意挖掘题目中的三点共线条件，灵活运用“定理”，以静制动、化陌生为熟悉，给我们求解带来了极大方便．精妙之极，展现了“定理”在解题中的神奇功效与魅力．

（五）在几何证明题中的巧妙运用

对一些比较复杂的几何证明题，善于挖掘三点共线条件，利用“定理”解决，不仅是一种全新的解题思路，更是一种有效的捷径．

1．平面几何问题的证明

例8如图6，在△ABC中，设D，E是BC的三等分点，D在B，E之间，F是AC的中点，G是AB的中点，又H是线段EG和DF的交点，求证：

图6

因为E，H，G三点共线，所以，依据“定理”，存在唯一实数λ，使得

因为D，H，F三点共线，所以，依据定理，存在唯一实数μ，使得

由①②，得

2.立体几何问题的证明

例9（2013年浙江卷理科20题）如图7，在四面体A-BCD中，AD⊥平面BCD，BC⊥CD，AD=2，，M是AD的中点，P是 BM的中点，点Q在线段AC上，且AQ=3QC.求证：PQ∥平面BCD.

证明：这是一道典型的将立体几何问题转化为平面几何问题证明的题目，但若用三点共线向量式来证明，过程会变得更加简洁明了.

连接A，P，交BD于N，连接CN，设A →P=λA →N（λ∈R），由P是BM的中点，有

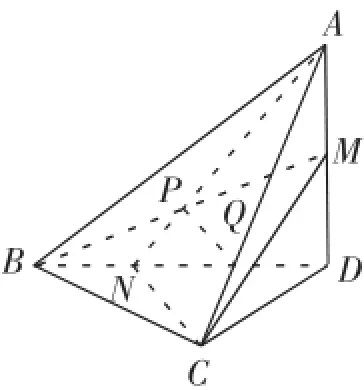
图7

评注：以上两个题若用平面几何知识证明，显得比较困难、烦琐，用向量法证明平面几何问题，把几何证明转化为向量运算，特别是三点共线向量式定理的充分运用，达到了化难为易，化繁为简的目的，大大缩短了解题过程，真可谓“四两拨千斤”.

（六）在解决有关范围问题中的巧妙运用

例10（重庆高2015级学业水平测试题第25题）已知P是

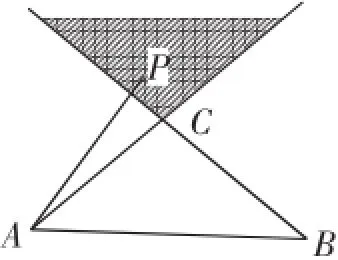
图8

解析：根据所给题目，容易看出这是一个“变异”的线性规划问题，即约束条件隐藏于向量条件之中.掀起向量盖头，挖掘隐藏在条件中的x，y满足的关系，是解决问题的突破口.

评注：本题中x的范围的确定是一个难点，但根据平面向量加法运算的平行四边形法则和三点共线向量式定理来确定，可谓行云流水，事半功倍，充分展现了“定理”在解题运用中的魅力与神韵.

通过以上各题解答我们看到，充分运用三点共线向量式定理这个基本工具来解决有关三点共线的方程、三角形、数列、几何、线性规划等题目时，大大简化了采用常规方法而产生的复杂的运算，使得过程简洁流畅.这种将平面向量的思想延伸到数学其他多个分支中，体现了“定理”在数学解题中极其重要的地位与作用，不仅仅是知识层面上的交汇，更重要的是思想上、方法上的交汇；不仅有效实现了数学知识和方法的整合，同时对于学生创新意识的培养大有裨益，值得大家认真领会与进一步探索.

1.蒋明建.善用“1”巧解数学题［J］.《高中数学教与学》，2010（4）.

2.蒋明建.破解向量难题挖掘潜在信息［J］.《中学数学》（上），2013（5）.

3.吴成强.三点共线向量式的巧妙运用［J］.《中学数学教学》（高中版），2010（5）.