基于变论域模糊控制的大豆种植灌溉控制算法

王 健，谢 南

(东北林业大学信息与计算机工程学院，哈尔滨 150040)

0 引 言

大豆是我国仅次于水稻，小麦，玉米的主要经济作物[1]，在全国范围内均有广泛种植，其中以东北地区最为出名。大豆是需水较多的喜温作物，每形成1 g干物质将消耗600～700 g水分，积温一般需要2 400～3 800 ℃[2]，对土壤条件的需求较低，对土质的适应能力较强。

以色列，美国，荷兰等农业发达国家早已将计算机，自动化控制等技术应用于农业生产过程中，已经形成了高投入高产出的生产模式[3]，而目前我国大豆种植过程中还多以大水漫灌，间歇灌溉等人工灌溉方式为主，自动化普及程度较低[4]。现有的自动化灌溉又多以传感器采集当前土壤墒情并与给定阈值进行对比灌溉的方式为主[5]，而阈值多采用符合作物生长规律的分段函数表示，与实际作物生长规律有一定差距。除此之外，由于作物灌溉所依赖的环境因素较多而大田环境又复杂多变，不易预测，是一种非线性、大惯性延时系统[6]，因此难以建立精准的数学灌溉模型。模糊控制是在专家经验的基础之上，能够在不依赖被控对象精准数学模型的情况下对被控对象实施操作的技术[7]，虽然它可以解决由于无法建立精准灌溉模型所带来的难题，但是其结构参数的选择往往相对固定，这导致在进行高精度控制时会出现控制规则过多，系统稳定性差，控制误差大等问题，因此无法进行精准灌溉[8]。

本文针对以上问题提出了一种将大豆各生长时期的需水规律和降雨量作为参考因素，通过变论域模糊控制技术动态调节灌溉时间的智能灌溉控制算法。本文控制算法在考虑了作物所处生长时期适宜土壤墒情的情况下，判断是否需要进行灌溉，如需灌溉则通过变论域模糊决策得到符合作物生长所需的灌溉时间并按值进行灌溉，执行灌溉的同时监测降雨量以便及时对灌溉进行调控；如不需要灌溉，则继续监测土壤墒情直至到达灌溉阈值，在等待过程中自动检测周期变化以便改变阈值。该算法可以有效改善因未考虑降雨量而未对灌溉进行动态调节所导致的过量灌溉问题，提高了自然降雨的利用效率，降低了水资源的浪费，保证了水资源的最大利用。

1 适宜土壤墒情的确定

大豆在不同的生长时期，对土壤的适宜墒情范围各不相同，因此为了制定符合大豆不同生长时期需水规律的灌溉制度，必须对大豆不同时期的需水规律进行了解。大豆的生长时期大体分为萌发期，幼苗期，分枝期，花荚期，鼓粒期以及成熟期这6个时期，根据文献[9]-[12]，我们总结出大豆各生长时期的持续天数以及根系主要分布土壤层的适宜土壤墒情范围(本文的土壤墒情均用土壤含水量与田间持水量的百分比来表示)，本文使用各土层适宜土壤墒情范围的平均值作为整个作物生长的适宜土壤墒情范围，具体如表1所示。

表1 大豆各生长时期持续天数及适宜土壤湿度范围Tab.1 Duration and suitable soil moisture range ofsoybeans each period

通过表1中各时期的适宜土壤墒情范围我们可以获得大豆生长的最佳土壤墒情变化曲线。最佳土壤墒情变化曲线是决定灌溉阈值的重要标准，传统的墒情变化曲线大多采用分段函数的形式表示，随生长时期的变化会表现出一定的跳跃性，但实际的土壤墒情变化应该是一个连续不间断的变化过程。比起间断跳跃的分段函数，处处连续的多项式函数可以更好地反应土壤墒情的变化，所以为了达到精准的效果本文使用多项式函数来表示土壤最佳墒情的变化曲线。

根据文献[13]的研究我们选取大豆生长的几个关键时期的最佳土壤墒情作为曲线拟合的关键点，设关键点的坐标为pi(xi,yi)(其中i=1,2,…,m)，原始曲线为y=F(x)，拟合的近似曲线为yi=P(xi)，令δi=P(xi)-F(xi)为曲线yi=P(xi)与曲线y=F(x)的偏差值。为了使偏差值的平方和I达到最小，即：

I=min∑mi=0δ2i=min∑mi=0[P(xi)-F(xi)]2

(1)

令多项式P(xi)=∑nk=0akxki式中n(n≤m)为多项式的最高阶数，得出：

I=min∑mi=0(∑nk=0akxki-yi)2

(2)

对项数aj(j≤n)求偏导数可得：

(3)

推导可得：

∑mi=0(∑nk=0xk+ji)ak=∑mi=0yixji

(4)

表示成矩阵形式可得到如下矩阵：

由于该矩阵是一个对称的正定矩阵，解是唯一的，所以可以通过该矩阵求得a0,…,an从而求得拟合的多项式yi=P(xi)。通过关键点的分布情况，设n=8，将n带入到上式中得到最佳墒情的拟合多项式曲线：

y=(2.192 e-13)x8-(1.255 e-10)x7+(2.926 e-08)x6-

(3.584 e-06)x5+0.002 497x4-0.010 21x3+0.248 2x2-

3.149x+79.88R2=0.957 8

(5)

具体曲线如图1所示。

图1 最佳土壤墒情变化曲线Fig.1 Change curve of optimum soil moisture

2 灌溉控制算法

2.1 变论域模糊控制

变论域模糊控制是具有自适应性的模糊控制，在保证控制规则数目不变的前提下，通过在传统模糊控制器中加入伸缩因子，以此对标准论域进行压缩(扩展)变相增加控制规则的数目，从而提高了整体的控制精度，增加了系统的稳定性，减小了控制误差[14-16]。因此为了实现精准灌溉，本文使用高控制精度的变论域模糊控制对灌溉时间进行控制。

2.1.1 变量论域

本文所使用的变论域模糊控制器是一个双输入单输出的模糊控制器，输入变量分别为土壤墒情传感器实际采集到的土壤墒情与该时刻最佳墒情的差值E以及土壤墒情的变化率ET，输出变量为灌溉操作的执行时间T。设变量E的取值范围在最佳墒情上下浮动10%，所以基本论域为[-10,10]，通过公式(6)。

(6)

将其转换到标准论域[-2,2]上，语言变量取值为负大(NB)，负小(NS)，适中(ZO)，正小(PS)，正大(PB)5个等级，论域量化值取{-2,-1,0,1,2}；ET的基本论域范围由专家经验获得，语言变量取值为小(NB)，较小(NS)，中(ZO)，较大(PS)，大(PB)，论域量化值取{0,1,2,3,4}5个等级；灌溉操作的执行时间T的语言变量取值为零(0)，短(NB)，较短(NS)，中 (ZO)，较长 (PS) 以及长 (PB)，论域量化值取{0,1,2,3,4,5}六个等级。各变量具体的赋值表如表2～表4所示。

表2 土壤墒情的赋值表Tab.2 Assignment table of soil moisture

表3 土壤墒情变化率的赋值表Tab.3 Assignment table of soil moisture change rate

表4 灌溉时间的赋值表Tab.4 Assignment table of irrigation time

为了获得模糊蕴涵关系RT(E,ET)，本文通过公式：

μ(x,y)=μ(x)∧μ(y)

(7)

式中：μ(x)与μ(y)表示模糊集合E与ET的隶属度函数；μ(x,y)表示其蕴含的模糊关系RT的隶属度函数；符号∧为取最小笛卡尔积对输入变量进行模糊推理。为了将模糊变量还原为准确的数值，本文通过公式：

μAi(U0)=max{μA1(U0),μA2(U0),…,μAn(U0)}

(8)

式中：集合Ai满足Ai∈F(U)，其中F(U)为所有模糊集合的隶属度函数，U0∈U对得出的模糊关系进行解模糊处理。

2.1.2 伸缩因子

有α(x)对于∀x∈X，满足α(x)=α(-x)，|x|<α(x)E且α(0)=ε,(且ε>0是一个非常小的数)对于∀x1,x2∈X，若|x1|<|x2|，则α(x1)<α(x2)，且α(±E)=1(其中X=[-E,E]是变量x的论域),则称α(x)为X上的伸缩因子。在控制规则数目不变的情况下，伸缩因子可以在不考虑隶属度函数形状的同时使论域随误差的减少(增加)而收缩(扩展)，相当于在局部范围内增加了模糊控制规则的数量，使插值节点更为紧密，大幅度提高了控制的精度。

求解伸缩因子是变论域模糊控制的关键步骤，常使用的计算方法包括比例形式法和指数形式法两种[17]，本文使用比例形式法进行伸缩因子的计算。设输入变量E,ET的伸缩因子分别为α(e)与β(et)，输出变量T的伸缩因子为γ(e,et)，通过公式(9) (10)

(10)

式中：τ,ε≥0分别对输入输出变量的伸缩因子进行求解。再通过公式(11):

(11)

求出新的输出变量。这样可以得到改变后的新论域范围，即<-α(e)E,α(e)E>,<-β(et)ET,β(et)ET>以及<-γ(t)T,γ(t)T>。

本文中调节的论域原则是当土壤墒情误差较小时对标准论域进行压缩，当土壤墒情误差较大时不对标准论域进行操作，这样可以使压缩论域集中在零点附近。伸缩因子的调节公式如(12)所示：

(12)

式中：θ为范围偏差的设定值；xb为标准值。

根据实际灌溉情况分析，本文取θ=1，β(et)=1，α(e)与γ(e,et)均按调节公式进行计算，这样我们可以通过论域细分有效解决传统模糊控制控制精度低，稳定性差等的问题。

2.1.3 模糊控制规则

当土壤墒情差值较大时，无论墒情变化率的多少都应及时进行补水灌溉(或是停止灌溉)；当土壤墒情差值较小时应根据墒情变化率的大小进行适当灌溉。根据上述内容，本文选用模糊条件语句IfxisA1andyisB1thenzisC1来进行模糊规则的表述，根据领域专家的经验我们总结出25条灌溉规则，具体如表5所示。

表5 模糊决策表Tab.5 Table of Fuzzy decision

根据表5的灌溉规则，我们可以获得如下查询表。

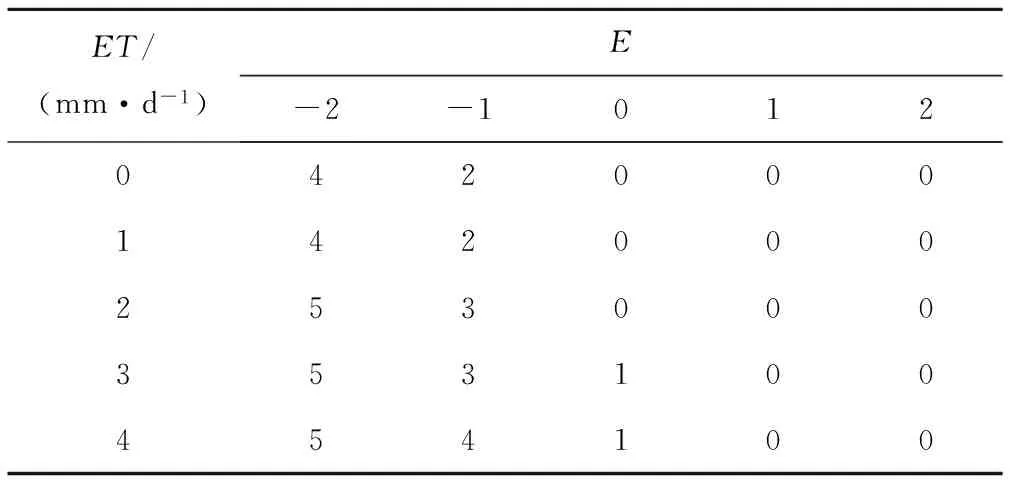
表6 模糊控制查询表Tab.6 Table of Fuzzy control inquiry

2.2 灌溉阈值的确定

大豆各生长时期的适宜土壤墒情以及对水分的敏感程度各不相同，充分利用作物的需水规律以及适宜土壤墒情来设定灌溉阈值是节水灌溉的关键所在。

(1)萌发期，出苗期前期，花荚期后期，鼓粒期以及成熟期是随日期的增加，对土壤墒情的需求呈下降态势，对土壤水分缺失的敏感程度较弱的时期。根据文献18的研究表明，萌发期进行轻度水分胁迫有利于前期干物质的积累；而出苗期前期进行轻度水分胁迫有利于大豆根系的深度生长；花荚期后期与鼓粒期进行轻度水分胁迫有利于干重增加，因此在以上时期对作物进行轻度水分胁迫不但不会抑制作物生长，还会在一定程度上促进作物发育。因此我们选择以上时期对应的适宜土壤墒情的下限值作为灌溉阈值(下限值如表1所示)，该数值为是否进行水分胁迫的临界值，选择该数值可以视为对作物进行轻度水分胁迫，可以有效减少灌溉次数，降低灌溉用水量，还可以在一定程度上防止由周期变换所导致的土壤墒情过高现象。

(2)出苗期后期，分枝期以及花荚期前期是随日期的增加，对土壤墒情的需求呈上升态势，对土壤水分缺失较为敏感的时期，应注意及时补水灌溉，使土壤墒情保持在较高的环境下。如果以最佳湿度作为灌溉阈值将导致灌溉操作执行过于频繁，增加系统耗能，降低整体的经济效益；而阈值选择过低将无法满足土壤高墒情的需求。为了使土壤墒情保持在较高的数值且在适宜墒情范围之中，我们选取以上时期的最佳土壤墒情向下浮动2%作为灌溉阈值(最佳土壤墒情由最佳土壤墒情变化曲线计算获得)，这样可以有效防止由于周期变换所带来的暂时性缺水问题。

2.3 灌溉控制算法

算法输入为播种后天数D，算法输出为灌溉时间T，具体描述如下：

(1)根据输入变量D判断大豆的生长时期是否结束，结束则算法结束，否则执行(2)；

(2)根据输入变量D确定作物当前所处的生长时期，执行(3)；

(3)根据生长时期查询对应的适宜土壤墒情范围以及最佳土壤墒情，执行(4)；

(4)根据生长时期选择灌溉方式并且确定灌溉阈值Ef，执行(5)；

(5)判断生长时期是否发生变化，发生变化执行(1)，否者执行(6)；

(6)监测当前土壤墒情E，执行(7)；

(7)判断E与阈值Ef的大小关系，小于则执行(8)，否则执行(16)；

(8)监测当前土壤墒情变化率ETC，执行(9)；

(9)判断ETC是否大于0，如果是则执行(10)，否则执行(15)；

(10)通过模糊决策计算灌溉时间T，执行(11)；

(11)按T进行灌溉，执行(12)；

(12)测得灌溉执行后的土壤墒情变化率ETB，并执行(13)；

(13)监测当前土壤墒情变化率ET，判断ET是否小于等于ETB-δ，如果是则执行(9)，否则执行(14)；

(14)判断灌溉操作是否执行完毕，是则执行(5)，否则执行(13)；

(15)停止当前一切灌溉操作，继续监测ET，执行(5)；

(16)判断E是否大于100%，是则执行(17)，否则执行(6)；

(17)执行排涝操作，执行(6)。

算法中δ是降雨的评判因子，如果δ较小表示当前降雨对土壤墒情变化的影响较小，可以按计算得出的时间执行灌溉操作，如果δ较大表示当前降雨对土壤墒情变化的影响较大，应该停止灌溉等待降雨停止再重新进行判定，根据实际种植环境，本文取δ=0.125。

具体算法流程图如图2所示。

图2 控制算法流程图Fig.2 Flow chart of control algorithm

3 仿真与实验

首先，在系统的响应时间以及稳定性方面，将本文的变论域模糊控制方案与传统PID控制方案以及传统的模糊控制方案进行对比，通过MatLab进行仿真实验，得到仿真曲线如图3所示。通过仿真曲线我们可以得出传统PID控制的响应时间为38.2 s，最大超调量为21.75%；传统的模糊控制的响应时间为26.7 s，最大超调量为14%；本文的变论域模糊控制方案的响应时间为14.3 s，最大超调量为9.75%。于此得出，相比于传统PID控制和传统的模糊控制方案，无论在系统的响应时间还是系统的稳定性方面，本文的变论域模糊控制方案均具有较好的控制效果。

图3 系统响应曲线Fig.3 Curve of system response

于2015年4月下旬在肇东市长富村进行灌溉试验，实验大豆品种为东升1号，播种开始前测得试验区域的土壤墒情为72%，气温为21 ℃ ，空气相对湿度为53%，西南风3～4级，具体灌溉方式以及参数如表7所示。图4为灌溉操作执行后实验大豆全生育周期内的土壤墒情变化情况，由图可知本文算法可以使实验大豆60%左右的时期生长在适宜墒情范围内；由于不同程度降雨的影响，剩余40%左右的时期土壤墒情超过了对应时期的适宜范围。全生育周期中累计有效降雨量约为367 mm，共执行6次灌溉操作，具体灌溉时间与灌溉量如表9所示。相比于表8所示的同时期该地区其他区域人工控制灌溉方式所用的灌溉量，本文方法可以节约20%的灌溉用水。

表7 灌溉参数Tab.7 Irrigation parameters

表8 人工控制灌溉量Tab.8 Irrigation volume of manual control

表9 本文方案灌溉量Tab.9 Irrigation volume of variable-universe fuzzy control

图4 土壤墒情变化曲线Fig.4 Change curve of soil moisture

4 结 论

本文在对大豆不同生长时期的需水规律进行分析的基础之上，结合降雨量提出了一种基于变论域模糊控制理论的大豆智能灌溉控制算法；首先使用多项式曲线拟合获得土壤最佳墒情的变化曲线，再通过大豆的生长时期确定灌溉阈值，最后结合降雨量运用变论域模糊控制技术对灌溉时间进行控制。通过仿真实验可以得到初步试验结论：

(1)本文通过多项式拟合得出的土壤最佳墒情变化曲线，相关系数为0.957 8，变化规律符合大豆不同时期的需水规律，可以较好地反映出土壤最佳墒情的变化过程。

(2)在响应时间方面，本文的变论域模糊控制方案的响应时间仅仅是传统PID控制方案的37.43%，是传统的模糊控制方案的53.56%；在最大超调量方面，本文方案的最大超调量仅仅是传统PID控制方案的44.83%，是传统的模糊控制方案的69.64%。因此，无论在系统响应时间还是系统稳定性方面本文方法均具有较好的控制效果，可以有效提高系统的稳定性以及控制的精度。

(3)通过模拟灌溉实验，本文的控制算法在考虑自然降水的情况下可以使大豆全生长周期55%以上的时期保持在适宜墒情范围内，相比于传统的人工控制灌溉方式可以有效地提高自然降雨的利用率，节约20%的灌溉用水，为大豆的节水灌溉提供了一条新的途径。

□

[1] 杨兆岿. 黑龙江省应对进口大豆产品影响的对策研究[D]. 哈尔滨：哈尔滨工业大学, 2010.

[2] 赵恩龙. 不同水分处理对大豆物质积累及土壤水分变化的影响[D].哈尔滨：东北农业大学,2014.

[3] 孙 静. 基于模糊控制的智能灌溉系统的研究[D].济南：山东大学,2014.

[4] 杨 晶. 基于MATLAB的智能灌溉模糊控制系统的研究[J]. 电脑知识与技术,2011,(9):2 143-2 144,2 147.

[5] 潘永安. 温室作物水分亏缺智能诊断系统研发[D].北京：中国科学院研究生院(教育部水土保持与生态环境研究中心),2014.

[6] 匡迎春,沈 岳,段建南,等. 模糊控制在水稻节水自动灌溉中的应用[J]. 农业工程学报,2011,(4):18-21.

[7] 李家春,王永涛,张 萍,等. 基于PC和C8051F的模糊灌溉控制系统[J]. 中国农村水利水电,2012,(4):61-63,71.

[8] 谢守勇,李锡文,杨叔子,等. 基于PLC的模糊控制灌溉系统的研制[J]. 农业工程学报,2007,(6):208-210.

[9] 王 丹,南 瑞,高永刚,等. 黑龙江省大豆产量与土壤湿度关系的研究[J]. 东北农业大学学报,2012,(5):105-109.

[10] 由剑波,陈志东,高兴民. 基于干旱区的大豆高效节水灌溉制度制定[J]. 黑龙江水利科技,2012,(1):82-83.

[11] 葛慧玲. 水分处理对大豆物质积累的影响及土壤水分模型构建[D].哈尔滨：东北农业大学,2013.

[12] 武荣盛,吴瑞芬,孙小龙,等 内蒙古东北部大豆灌溉动态预报模型[J]. 干旱地区农业研究,2015,(3):35-39.

[13] 毛洪霞. 滴灌大豆需水规律及灌溉制度的研究[D]. 陕西杨凌：西北农林科技大学,2008.

[14] 李洪兴. 变论域自适应模糊控制器[J]. 中国科学E辑:技术科学,1999,(1):32-42.

[15] 牛 寅,张侃谕. 轮灌条件下灌溉施肥系统混肥过程变论域模糊控制[J]. 农业机械学报,2016,(3):45-52.

[16] 李 琳,周国雄. 基于逆模型解耦的绿茶烘焙变论域模糊控制[J]. 农业工程学报,2014,(7):258-267.

[17] 邵 诚,董希文,王晓芳. 变论域模糊控制器伸缩因子的选择方法[J]. 信息与控制,2010,(5):536-541.

[18] 庞艳梅. 水分胁迫对大豆生长发育、生理生态特征及养分运移的影响[D].北京：中国农业科学院,2008.