例谈数列通项公式的求法

☉山东省肥城市泰西中学 王瑛泽

例谈数列通项公式的求法

☉山东省肥城市泰西中学 王瑛泽

数列在理论上和实践中均有较高的价值，是培养学生观察能力、理解能力、逻辑思维能力的绝好载体.高考对数列知识的考查逐渐升温，随着与大学知识的接轨，竞赛题的释放，很多省市的高考数学卷都把数列题作为压轴题，而数列通项公式的求法又成为一个热点.笔者通过多年的教学实践，总结一下在高中阶段，求数列的通项公式的常用方法和策略.

一、公式法

直接利用等差数列或等比数列的定义求通项，或者已知第n项与前n项和的关系求解，用公式法求数列通项公式包括三种类型：

（1）用等差数列的通项公式an=a1+（n-1）d求解；

（2）用等比数列的通项公式an=a1qn-1求解；

例1等差数列｛an｝是递增数列，前n项和为Sn，且a1，a3，a9成等比数列.求数列｛an｝的通项公式.

解：设数列｛an｝公差为d（d＞0），

由于a1，a3，a9成等比数列，则=a1a9，

即（a1+2d）2=a1（a1+8d）⇒d2=d.

又d≠0，故a1=d.①

因为S5=·d=（a1+4d）2.②

例2已知数列｛an｝的前n项和Sn满足Sn=2an+（-1）n，n≥1，求数列｛an｝的通项公式.

解：由a1=S1=2a1-1⇒a1=1.

当n≥2时，有an=Sn-Sn-1=2（an-an-1）+2×（-1）n，

所以an=2an-1+2×（-1）n-1，an-1=2an-2+2×（-1）n-2，…，a2= 2a1-2.

所以an=2n-1a1+2n-1×（-2）n-2+…+2×（-2）n-1

=2n-1+（-1）n［（-2）n-1+（-2）n-2+…+（-2）］

经验证a1=1也满足上式，所以

二、模型法

当所给数列的递推式满足一定的模型，可以按照一定的方法解决.

1.形如an+1=ban+c或an+1=ban+f（n）或an+1=ban+cn

递推式形如an+1=ban+c或an+1=ban+f（n）或an+1=ban+cn，其中b，c为不相等的常数，f（n）为一次式，可以构造等比数列.原数列｛an｝既不等差，也不等比，若把｛an｝中每一项添上一个数或一个式子构成新数列，使之等比，从而求出an.

例3设数列｛an｝的首项a1∈（0，1），an=，n≥ 2，n∈N*，求｛an｝的通项公式.

解：构造新数列｛an+p｝，使之成为的等比数列，即（an-1+p），整理得p满足an=，故p=-1，即新数列｛an-1｝首项为a1-的等比数列，则

2.形如an+1=ban+bn+1+f（n）

递推关系式形如an+1=ban+bn+1+f（n），可以构造等差数列.数列｛an｝既不等差，也不等比，那么把两边同时除以bn+1后，想方设法构造一个等差数列，从而间接求出an.

例4数列｛an｝满足an+1=-2an+（-2）n+1（n∈N*），首项为a1=-2，求数列｛an｝的通项公式.

解：an+1=-2an+（-2）n+1，两边同时除以（-2）n+1，得

故an=n（-2）n.

3.形如an-an-1=f（n）（n≥2，n∈N*）

对于形如an-an-1=f（n）（n≥2，n∈N*）且f（1）+f（2）+…+f（n-1）可求时，则用累加法求an.有时若不能直接用，可变形成这种形式，然后用这种方法求解.

例5在数列｛an｝中，a1=1，an-an-1=n-1（n≥2，n∈N*），求｛an｝的通项公式.

解：当n=1时，a1=1；

4.形如an+1=anf（n）

对于递推公式为an+1=anf（n）的形式，采取累乘法.一般把原递推公式转化为=f（n），利用累乘法求解.

例6已知数列｛an｝满足求an的通项公式.

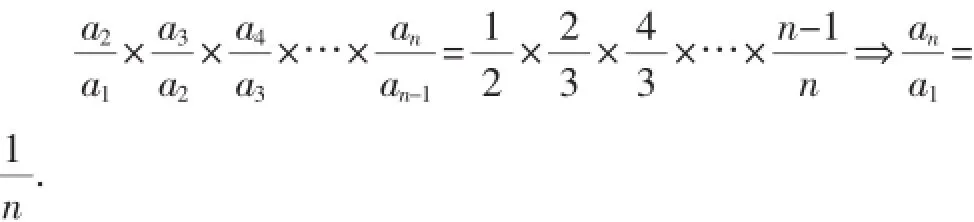
例7已知数列｛an｝，a1=-1，an+1=，n∈N*，求数列通项an.

解：把原式变形得an+1-an+1·an=an，两边同时除以anan+

1，得+1，所以是首项为-1，d=-1的等差数列，故=-1+（n-1）（-1）=-n，因此

6.形如an+1=f（n）.

对于形如an+1=f（n）的递推式要用到对数进行转化，两边取常用对数lgan+1=lg（fn）+Algan.

例8在数列｛a｝n中，an+1=2·3n·，a1=7，求数列｛a｝n的通项公式.

解：因为an+1=2·3·n，a1=7，所以an＞1.

在an+1=2·3n·两边取常用对数lgan+1=lg2+nlg3+5lgan，令bn=lgan，余略.

例9在数列｛an｝中，a1=1，8an+1an-16an+1+2an+5=0，求an.

（此处可以利用函数的不动点知识对题中的λ的求法进行算法改进，它的不动点为

以下可参照形式5，求出bn，从而得到

由数列的递推关系求通项公式的情况很复杂，立足于等差、等比数列的基础，借助线性关系、对数关系、倒数关系、函数知识等，进行数学问题的化归转化，就能将问题很好解决.

三、解方程组法

例10已知数列｛an｝，｛bn｝满足a1=300，求数列｛an｝，｛bn｝的通项公式.

解：当500λ+μ≠0时，可得

（1+λ）an+λbn+μ=0.8an-1+0.3bn-1+500λ+μ.

1.6an+0.6bn-600=

由1.6a1+0.6b1-600=1.6×300+0.6×200-600=0，得1.6an+0.6bn-600=0，1.6an+0.6bn=600.

四、构造常数列法

例11在数列｛an｝中，a1=1，其前n项和Sn满足nSn+1-（n+3）Sn=0，求数列｛an｝的通项公式.

解：把nSn+1=（n+3）Sn，（n+1）Sn+2=（n+4）Sn+1相减，得

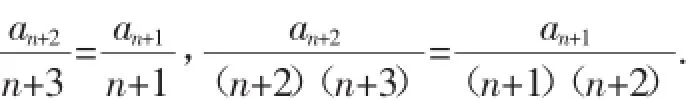
总之，求数列通项公式的方法并不满足以上所述，对于同一问题的求解也不仅是一种方法，只有在平时学习与探究过程中不断地体会与总结，将知识与方法学活，才可以做到游刃有余.