一次“微”教研引发的思考——基于一道题解法的讨论

☉江苏省南京市大厂高级中学 仝 建

一次“微”教研引发的思考
——基于一道题解法的讨论

☉江苏省南京市大厂高级中学 仝 建

一、问题提出

教师需要在教学实践中不断反思、研究，教师的教研活动可以渗透到工作的每一个环节，可以是饭桌旁与同事的聊天，可以是批改试卷时的讨论，我们不妨称之为“微”教研.在一次学校例会间隙，一位年轻的H教师对一道题目的答案不太确定，向邻座的老教师C请教，旁边的Z老师也参与其中（我校开会时，同学科老师坐在一起）.笔者倾听并参与讨论，深有感触，随后整理成文，谈谈自己的几点思考.

二、题目及解法讨论

题目过椭圆x2+2y2=a2（a＞0）的右焦点F作斜率大于0的直线与该椭圆相交于A，B两点.若点F将线段AB分成2∶1两段，则直线AB的斜率为___________.

这是笔者所在学校高三一轮复习讲义上的一道题.

Z老师首先对这道题谈了自己的做法和遇到的困难.

Z教师：我是设AB的方程为点斜式，然后联立直线与椭圆的方程，如果求出点A、B的坐标再用两点间距离公式的话，计算量太大，所以想借助韦达定理，对点A、B的坐标设而不求，但发现“点F将线段AB分成2∶1两段”不太好用韦达定理，况且会产生三个方程，四个未知数，所以没算出来.

评析：Z教师草稿纸如下：不妨设点A在x轴上方，设直线AB的方程为y=k其中k＞0，记A（x1，y1），B（x2，y2），联立直线AB和椭圆的方程，消去y得（2k2+1）x2-k2ax+k2a2-a2=0，由韦达定理得x1+x2=②，由BF=2AF，结合图形知y2=-2y1，所以有ka-x2=③（下面没有写下去）.笔者后来演算发现Z教师的解法可以继续下去，关键是如何由①②③式求出k的值，虽然三个方程含有四个字母，但估计a不会影响k的值，所以有信心算出k.由③式得x2=a-2x1代入整理得x1=④，从而x2=⑤，这样消掉了两个未知数x1，x2，将④⑤代入②可以消去a，得（说明前面的估计是正确的）.又因为k＞0，所以直线AB的斜率为这样用Z教师的方法就算出了答案.事实上，若设直线AB的方程为x=my+，其中m为直线AB的斜率的倒数.再联立直线AB和椭圆的方程，计算量要比Z老师的方法要小一些.

评析：与Z老师的设直线方程法相比，H老师的向量法计算量要小一些，我们通过演算得到方程组⑥的解为，即A所以直线AB的斜率kAB=kAF=，从而得出答案.H老师出现了一个计算的错误，并且发现结果有问题，所以才向C老师请教的.

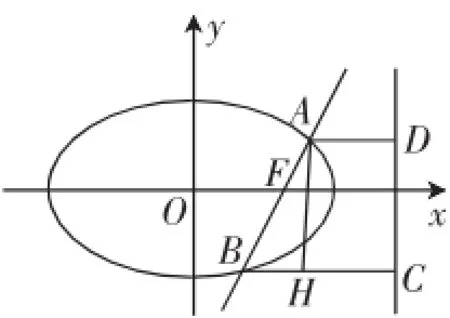
图1

C教师：我是借助圆锥曲线的统一定义，然后再构造直角三角形来做，可以口算出来.如图1，过A，B两点向右准线作垂线，垂足分别为D，C，再过点A作AH⊥BC，垂足为H.不妨设AF=1，由BF=2AF，得BF=2，AB=3，由圆锥曲线的统一定义，知，所以AD=，同理BC=2，所以BH=，AH=.得tan∠ABH=，从而得直线AB的斜率.

评析：C老师的解法借助平面几何的知识（构造了直角三角形）和圆锥曲线的统一定义，极大地简化了计算量，其中还采用了“不妨设AF=1”，用小量表示大量的技巧，所以可以快速口算出.

T教师（笔者）：我想到过焦点之弦，极坐标为宜.所以我是用极坐标做的，以椭圆的右焦点为极点，以x轴正向为极轴建立极坐标系，则椭圆的极坐标方程为ρ=.不妨设点A在x轴上方，记直线AB的倾斜角为，由BF=2AF，得.又由椭圆的离心率为，解得cosθ=，所以得tanθ=，即直线AB的斜率为

评析：极坐标方程解决圆锥曲线与焦点有关的弦长问题时，颇有优势，T教师和C老师的解法都避免了椭圆方程中参数a的干扰，简化了运算.

笔者在会后又得出另一解法，过已知点直线，可以借帮助直线参数方程中t的几何意义处理，为减少运算量，不妨设a=2，得点F的坐标为（，0），直线AB的参数方程为（t为参数），其中θ为直线AB的倾斜角.代入椭圆方程整理得（cos2θ+2sin2θ）t2+2cosθ·t-2=0，由韦达定理及BF=2AF，知t2=-2t1，t1·t2=，消去t1，t2得tan2θ=.又因为直线AB的斜率大于0，所以tanθ=，得解.

评析：过已知点直线有关线段长度问题，可以借助直线参数方程中t的几何意义去处理，但这种方法会涉及三角计算，有时会有一定的计算量，上述五种方法比较来看，C老师的平面几何结合圆锥曲线统一定义法与T教师的极坐标方程法较为简捷.

三、几点思考

1.解题方法的选择总是基于解题者已有的知识结构

拥有不同的知识结构，会选择不同的方法，特别是对于方法多样的问题尤为如此.Z老师和H老师一直教文科，对理科的极坐标方程法和直线的参数方程法不熟悉，自然不易想到，或即使想到，因为缺少此种方法的解题经验，也不敢在时间紧张的时候使用.学生在高三复习阶段更是如此，很少有学生愿意在一道题目上耗大量的时间思考.C老师有几年初中数学的教学经验，特别擅长平面几何，所以在解题时，他更容易想到借助平面几何简化运算.T老师刚教过一轮理科，对理科的极坐标方程法和直线的参数方程法应于解决解析几何问题情有独钟.教师对解题方法的选择是基于自己的知识结构，学生自然也是如此.

2.切实提高教师自身的解题、研题能力

《孟子·尽心下》中说“贤者以其昭昭，使人昭昭.”要引导学生学会解题，必然要求教师对题目有深入的理解，有较强的解题、研题能力.古人云，打铁还需自身硬，我们无法交给别人自己没有的东西.若教师的解法少，甚至只是看看参考答案，不进行独立的解题活动，研题能力不强，势必导致解题教学时捉襟见肘.文科教师懂得一些理科的方法，对深化自己对学科知识的理解，预见解题方向会有一定的帮助.教师独立解题经验越丰富，解法越多样，研题越深刻，在解题教学中，越能信手拈来，腾出更多的时间和精力关注到学生，进行教学艺术处理.

3.教解题要考虑学生的实际状况

H老师和Z老师的解题方法是不少文科学生“想得到”、“下不去”、“易出错”的方法，学生的真正困难在哪里？（看着目标消元与解方程组）教师要深入研究，争取给予学生必要的指导，帮助学生走出计算繁杂的泥潭.切不可置学生的真困难于不顾，另辟“蹊径”，教给学生新方法.否则，教师的新方法无法融入学生的认知结构中，学生的解题能力无法得到有效提升.

4.寻求“通法”和“巧法”的平衡

用代数的方法解决几何问题（几何问题代数化）是求解析几何问题的通法，如本文中H老师和Z老师的解法和笔者借助椭圆极坐标方程的方法.借助平面几何的知识求解析几何看似是巧法，如C老师的解法.但在求解析几何问题时，采用纯代数化的方法，有时会出现，理论上是对，但由于计算繁杂，耗时，导致中途出错，无法求出最终结果的情形.这就需要通法与巧法的平衡，既要关注通法，也不忽视巧法，实际上巧法在某种意义下也是通法，只是这种方法在某种情景下使用的频率少一些罢了.Z老师的解法中就需要加入一些“巧法”（如，估计a不会影响k的值，对a取特殊值，看着目标消元，设直线AB的方程为x=my+等），否则计算就难以到底.C老师的“巧法”借助平面几何知识（“巧法”）和圆锥曲线的第二定义，和T老师的“焦点之弦，极坐标为宜”（也是“巧法”）简化了计算.教师在解题中，要寻求“通法”和“巧法”的平衡.

5.注重新课教学的纵横交错

新课教学，切莫忽视用新方法解决老问题，这也是智慧发展的渠道之一.事实上，较少教师（即使是理科教师）采用椭圆极坐标方程法、直线参数方程法解题.不少教师在选修4-4极坐标和参数方程教学时，认为只需让学生学会参数方程、极坐标方程与普通方程的互化，会把参数方程、极坐标方程问题化为普通直角方程解决就可以了，淡化了参数方程、极坐标方程在研究解析几何问题中的作用，未能注意知识间的纵横联系，缺乏用新方法解决旧问题的意识，约束了学生解题时的思维触角.

四、结束语

做好解题教学，首先要求教师有较高的解题能力，需要老师勤于解题、研题，提高自己的解题功力，深化对数学学科的理解和掌握，肚子里要有货.好的解题教学，更要契合学生的实际情况，能和学生原有的认知结构搭上桥，还要考虑学生的情绪和情感状态，要“贴地”而行，接上学生的“地气”.好的解题教学，还要寻求恰当的方式保证教学渠道的畅通、有趣、积极、高效，这需要教师在解题教学过程中“各显神通”，进行艺术的处理.F