巧用构造法证明竞赛中的不等式

江西省新干中学 (331300) 曾自根

巧用构造法证明竞赛中的不等式

江西省新干中学 (331300) 曾自根

不等式的证明方法很多，巧而且灵活，其中构造法是不等式证明中的一种重要方法，即引入适当的恒等式，结合函数、图形、数列等辅助手段，将命题转化，变成较为直观和本质的形式，进而使不等式获证.本文撷取竞赛题中的几道不等式加以说明.

一、构造恒等式

证明：由海伦公式，有

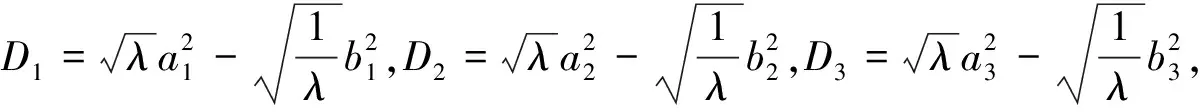
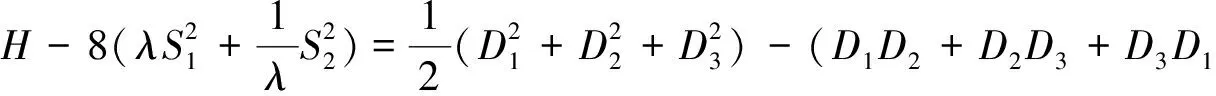
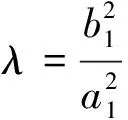
故结论成立.

评注：恒等式可以看作是最强的不等式，有时候，通过补充不等式中省去的那些项或因式，可以得到隐藏在其背后的恒等式，这样往往可以找到证题的突破口，因为恒等式的结果是显然的.

二、构造函数

我们可以根据代数式的特征，构造适当的函数.如一次函数，二次函数再利用函数性质证明不等式.

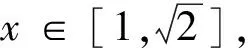
评注：通过换元，简化了欲证不等式.利用函数的单调性，以及求函数最值的方法使不等式简捷获证.

三、构造图形

若问题中的数量关系有明显的几何意义或以某种方式可与几何图形建立关系，那么可以通过作图构造图形，然后在图形中寻找所证的结论.

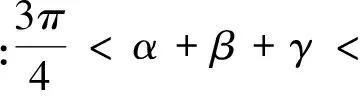
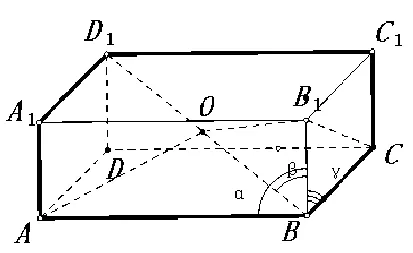
图1

证明：由条件，作一个长、宽、高分别为cosα、cosβ、cosγ的长方体ABCD-A1B1C1D1.如图1所示，AB=cosα，BC=cosβ，BB1=cosγ.则此长方体对角线长恰为1.同时，易见∠ABD1=α，∠CBD1=β，∠B1BD1=γ.

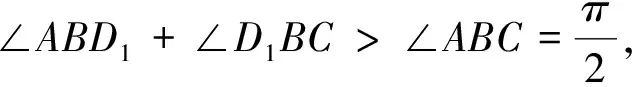
评注：有时可以观察所证不等式结构和特点，通过构造适当几何图形来辅助证明.

四、构造数列

例4 设ai为正实数(i=1，2，…，n),令kbk=a1+a2+…+ak(k=1,2,…n),Cn=(a1-b1)2+(a2-b2)2+…+(an-bn)2，Dn=(a1-bn)2+(a2-bn)2+…+(an-bn)2，求证Cn≤Dn≤2Cn.

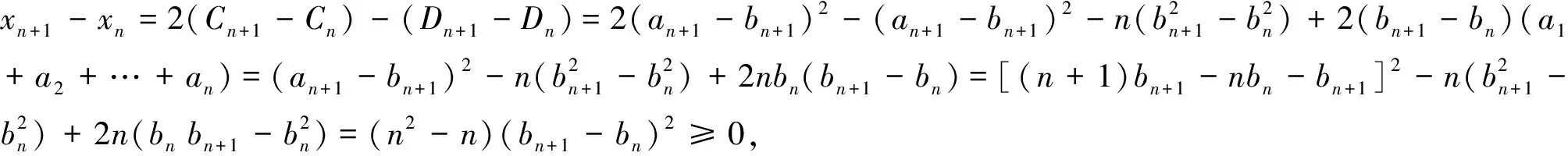
又由于x1=2C1-D1=(a1-b1)2=0，故对一切n，xn≥0.

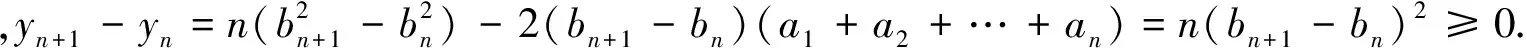
∴yn+1≥yn.

又y1=b1-c1=0，故对一切n∈N+,yn≥0.

综上所述Cn≤Dn≤2Cn.

评注：在遇到与自然数n有关的命题时，可以考虑构造辅助数列，并利用数列的性质证明与其相关的不等式.