改造陈题 推陈出新——2016年全国卷Ⅰ理科20题简析

福建省龙岩第一中学 (364000) 章金玲

改造陈题 推陈出新
——2016年全国卷Ⅰ理科20题简析

福建省龙岩第一中学 (364000) 章金玲

题目 设圆x2+y2+2x-15=0的圆心为A，直线l过点B(1,0)且与x轴不重合，l交圆A于C，D两点，过B作AC的平行线交AD于点E.

(Ⅰ)证明|EA|+|EB|为定值，并写出点E的轨迹方程；

(Ⅱ)设点E的轨迹为曲线C1，直线l交C1于M,N两点，过B且与l垂直的直线与圆A交于P,Q两点，求四边形MPNQ面积的取值范围.

2016年全国卷Ⅰ理科第20题，以圆为载体、课本中的轨迹问题为基本素材、类似于2005年全国卷中的一道四边形面积求解问题为主体，对其进行了合理的加工、重组、改造、“包装”.一方面，开辟了椭圆生成方法的新途径；另一方面，又将圆与椭圆(圆生成的轨迹)有机地融合在一起(全国卷的鲜明特点)，为考生创设了一个陌生的情景，考查学生将已有知识与方法灵活运用于新情境的迁移能力，真正做到了“以本为本、陈题不旧、推陈出新”，堪称一道“源于课本，高于课本”，自然、和谐，让人耳目一新的一道好试题．

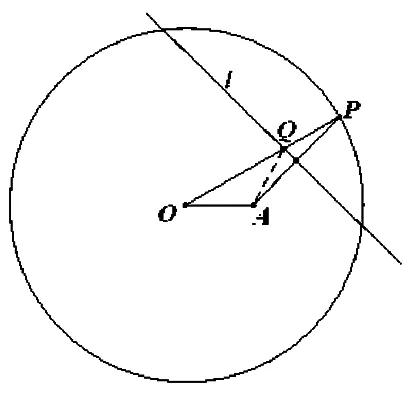
图1

一、试题背景探究

背景1 (人教A选修2-1P49习题2.2A组第7题)如图1，圆O半径为定值r，A为圆O内一个定点，P为圆上任意一点，线段AP的垂直平分线l与半径OP相交于点Q，当点P在圆上运动时，点Q的轨迹是什么？

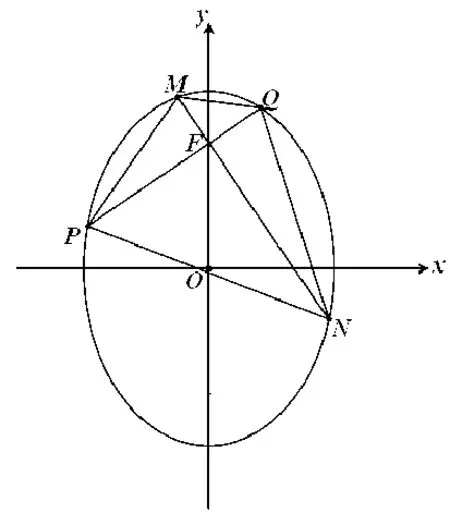
图2

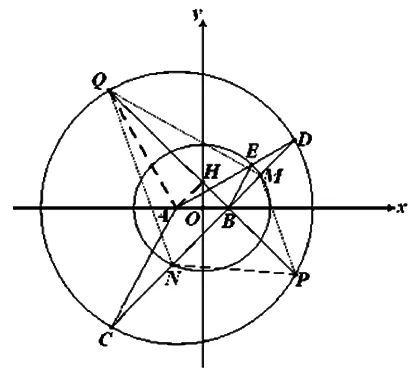
图3

简析：本题的第一问或取材于背景1，如图3，将课本习题中的图，延长PA交圆O于点B，连结OB，QA，再删掉直线l.明显的，两种轨迹的生成方法具有等效性，事实上，根据线段垂直平分线的性质，得|QA|=|QP|，∴∠P=∠QAP，又OP=OB，∴∠B=∠P，于是∠QAP=∠B，因此BO∥AQ，反之亦然．…如此形成的高考题第(Ⅰ)小题，注重平面几何知识的灵活运用，具有一定的新意，同时又为第(Ⅱ)小题的命制铺平了道路，过渡非常自然，衔接得非常完美.

本题的第Ⅱ问或来源于背景2，其四边形面积表达式的探求，以及取值范围的求解方法，两道试题大致相同.

二、解题方法探究

本题的第(Ⅰ)小题，着重考查学生对椭圆定义的理解，以及轨迹问题的求解方法，它具有很好的区分功能.第(Ⅱ)小题，主要考查直线与圆锥曲线的位置关系，以及最值的计算，考生既要计算椭圆中的焦点弦长，又要计算圆中的弦长，对他们的运算求解能力、综合分析能力等都提出了较高的要求.本小题解法多种多样，考生若用传统方法，计算比较繁琐，苦不堪言；若用参数方程或极坐标的知识去求解，则简洁得多.

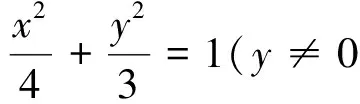
(Ⅱ)(法一)当l与x轴不垂直时，设方程为y=k(x-1)(k≠0)，M(x1,y1)，N(x2,y2).

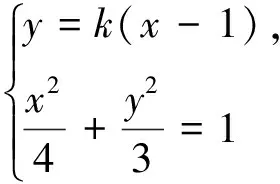
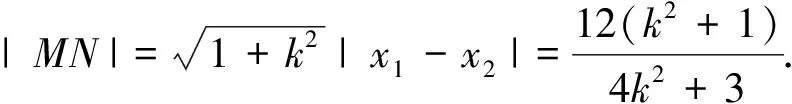
(法二)设直线l的参数方程为

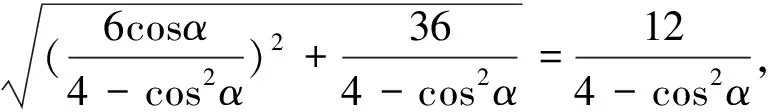
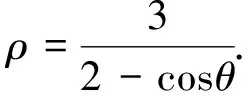
三、试题的引申

根据上面的几种解法及讨论，我们不难将它推广到一般情形，即

性质1 设圆(x+c)2+y2=4a2(a>0,c>0)的圆心为A，直线l过点B(c,0)且与x轴不重合，l交圆A于C，D两点，过B作AC的平行线交AD于点E.

(Ⅰ)证明|EA|+|EB|为定值；

(Ⅱ)设点E的轨迹为曲线C1，直线l交C1于M,N两点，过B且与l垂直的直线与圆A交于P,Q两点，则四边形MPNQ面积的取值范围为[4b2,4ab).

证明：(Ⅰ)因为|AD|=|AC|，EB∥AC，故∠EBD=∠ACD=∠ADC，所以|EB|=|ED|，故|EA|+|EB|=|EA|+|ED|=|AD|=2a，为一定值.

∴0≤cos2α<1，∴S∈[4b2,4ab).

性质2 设圆(x+c)2+y2=4a2(a>0,c>0)的圆心为A，直线l过点B(c,0)且与x轴不重合，l交圆A于C，D两点，过B作AC的平行线交AD于点E.

(Ⅰ)证明|EA|+|EB|为定值；

(Ⅱ)设点E的轨迹为曲线C1，直线l交C1于M,N两点，过A且与l垂直的直线与圆A交于P,Q两点，则四边形MPNQ面积的取值范围为[4b2,4a2).

证明留给读者.