“为迁移而教”
——以基本不等式教学设计为例*
华中师范大学数学与统计学学院 (430079) 王 静华中师范大学教师教育学院 (430079) 胡典顺
“为迁移而教”
——以基本不等式教学设计为例*
华中师范大学数学与统计学学院 (430079) 王 静华中师范大学教师教育学院 (430079) 胡典顺
一、引言
学习是一个连续的过程,任何学习都是学习者在已有知识经验基础上进行的,学习者原有的认知结构、知识经验、技能和态度对新的学习产生影响,新知识的学习过程及结果又会对学习者原有的认知结构进行改组,对原有知识经验进行扩充,对原有技能进行强化,这种新旧学习的相互影响就是学习的迁移,准确地说,一种学习对另一种学习的影响叫做学习迁移[1].可见,迁移贯穿于学生的学习过程中,学生的学习离不开迁移.教师不可能将学生需要掌握的所有东西一一教给学生,很多的学习过程可以通过迁移来实现.学习者已经具有的经验可能有助于顺利解决当前的问题,也有可能会起阻碍作用,因此,在教学中,如何促进学生产生更多的正迁移、避免负迁移是教师值得深思的问题.
数学知识具有内在的逻辑性、系统性,教材编写遵循循序渐进、螺旋上升的原则,前面学习的内容对后面的内容都有直接或间接的影响;高中阶段的四大数学思想方法:数形结合、分类讨论、函数与方程、转化(化归)以及换元法、数学归纳法、参数法、反证法等数学方法也都是在不同的知识内容中有相应的用法,学生如果掌握得好就会对后面的学习产生正迁移.除知识、思想、方法之外,技能、能力、情感、态度的学习同样可以通过迁移实现.课堂教学是学生学、教师教的主阵地,把以上这些内容的迁移设置在课堂教学的各个环节中,是培养学生学习迁移能力的一种有效方式.在课题导入环节,要精心设计问题的情境,激发学生求知的兴趣并创设学习的疑问;探究新知环节,使探究和迁移紧密联系,深化对新知识的理解;在练习巩固环节中,可以从与例题相似的题目入手,设置变式让学生更好地掌握新知识,防止学生运用新知识时犯错误;在拓展延伸环节中,可以拓展学生的思维,有效地优化数学教学的效果,引导学生总结归纳、完善数学认知结构.
二、基本不等式教学设计
1.情境迁移,导入新课
(1)展示第24届国际数学家大会的会标并介绍设计的相关背景(图1),引导学生找出这个会标中包含的几何图形,它的设计依据是赵爽弦图(图2).

图1 图2 图3
(2)利用几何画板改变弦图中直角三角形的两条直角边边长,展示变化过程,让学生观察、归纳出S大正方形≥4S直角三角形这个不等关系,即a2+b2≥2ab,引导学生分别从式子中和图形中探究等号成立的条件.图中a、b为直角三角形的边长,因此是正实数,设置问题“对任意实数a、b,a2+b2≥2ab都成立吗?”学生用配方法很快能完成证明.


2.知识迁移,形成结论
(1)探究1:基本不等式的证明
让学生自主探究,预设三种证明方法:作差法;分析法;综合法.
(2)探究2:基本不等式的代数意义与几何意义


(3)探究3:基本不等式链
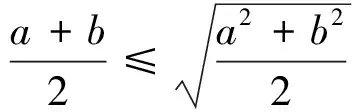
设计意图:探究1引出基本不等式的概念及式子之后,引导学生对基本不等式进行自主证明、交流讨论,让学生在相互交流中掌握不同的证明方法.探究2从代数和几何两个方面探究基本不等式,“数”和“形”是数学学习的两个重要对象,两者的相互转化可以为数学问题的研究提供广阔的思路.借助图形形象直观地促进学生对基本不等式的代数理解,基本不等式的代数式则有助于更深入地理解其几何意义,“数缺形时少直觉、形缺数时难入微”正是对“数”与“形”相互迁移的描述,两者之间的这种正迁移能帮助学生更好地理解基本不等式.探究3的设置旨在让学生掌握基本不等式链,揭示几个不等式之间的联系,优化学生关于不等式的数学认知结构,有利于学生在后面的学习中更好地实现数学知识的迁移.
3.习题迁移,深化认识




例2 (1)用篱笆围一个面积为100m2的矩形菜园,问这个矩形的长、宽各为多少时,所用篱笆最短,最短的篱笆是多少?
(2)一段长为36m的篱笆围成一个矩形菜园,问这个矩形的长、宽各为多少时,菜园的面积最大,最大面积是多少?
设计意图:学习迁移现象在数学教学中广泛存在,学习兴趣、学习态度、学习方法、知识、技能、数学思想、能力等都是可以迁移的.习题的迁移也是常见的,我们常说的举一反三、触类旁通在数学解题中就是对习题迁移的描述.例1之后设置三个变式让学生注意基本不等式使用的条件“一正二定三相等”,防止学生在运用基本不等式时忽略使用条件,避免负迁移的产生,尽可能地防止学生在后面的解题中犯错误.通过例2概括出基本不等式中“积定和最小、和定积最大”的规律,培养学生的概括能力.学生对已有知识的概括水平越高,就越能揭示同类知识的实质,把新知识纳入已有的数学认知结构中,实现对新知识的同化或顺应,从而发生正迁移.
4.能力迁移,发展思维


设计意图:不等式是高中数学的重、难点,在基本不等式的教学中,让学生了解与基本不等式相关的其他不等式有利于更好地掌握知识的内在结构,在数学教学中,教师应启发学生掌握知识的内在结构的相互联系.让学生了解柯西不等式、重要不等式、基本不等式、均值不等式之间的关系,可以让学生对不等式这个内容有更高层次的理解,从而优化学生对不等式的认知结构,在后面的学习中产生更多的正迁移.
三、结语
迁移的实质是概括,概括性越强迁移范围就越广;迁移的基础是联系,只有相互有联系才能相互影响;迁移的实现是联想,只有从问题联想到已经掌握的知识技能,才能找到解决问题的策略[2].因此,教师应该注重培养学生的概括能力,学生对已有的知识、经验的概括水平越高,就越能把新知识纳入已有的认知结构中,促进正迁移的产生.在数学教学中,教师应启发学生找出那些具有高概括性、包摄性的基本概念和原理,掌握知识的内在结构的相互联系,这样既可以简化知识,又可以灵活运用知识和产生新知识[3].教师还应强调基础知识和基本技能的获得,因为要学习的新东西与学生已经掌握的基础知识和基本技能之间存在联系,只有掌握好基础知识和基本技能,作为迁移的基础的这种联系才能促进正迁移.同时,基础知识和基本技能还是实现联想的基础,没有扎实的基本功,学生很难由问题联想到认知结构中相关的知识、技能、方法等,问题就难以得到解决.迁移现象存在于课堂教学的各个环节,教师可以将各种迁移的策略、迁移理论融入进高中数学教学的过程中提高学生的学习迁移能力.教师无法代替学生习得迁移能力,需要做的是在课堂教学中为学生提供更好的迁移条件,精心设计好每一堂课,鼓励学生发现问题、提出问题,为学生指明迁移的方向.
总之,作为教学活动的组织者、学生学习的促进者,教师要遵循“为迁移而教”的教学理念,创设高效率的课堂教学活动.让课堂多一些有意义的学习,少一些机械的学习,在最近发展区中最大限度地促进学生知识、技能、情感、态度等方面的迁移,创造迁移氛围、提高学生的学习迁移能力.
[1]喻 平.数学教育心理学[M].南宁:广西教育出版社,2004.
[2]马 波.迁移规律在中学数学教学中的运用[J].课程·教材·教法,2003(12):29-32.
[3]朱华伟,张景中.论数学教学中的迁移[J].数学教育学报,2004,13(4):17-19.
全国教育科学规划教育部重点课题——TPACK视角下卓越教师培养的理论研究与实践探索(课题编号DHA150287).

