例谈一题多变与一题多法的解题教学*——消除“懂而不会”现象的两种有效教学方法

江苏省睢宁高级中学北校 (221200) 徐存新 武瑞雪

例谈一题多变与一题多法的解题教学*
——消除“懂而不会”现象的两种有效教学方法

江苏省睢宁高级中学北校 (221200) 徐存新 武瑞雪

1 一题多变

1.1 “一题多变”含义、作用及案例点评

“一题多变”是指变换原题目的条件或结论，得到一些新题目，是对某一类题目固化某一种解法，利于加深学生对所涉数学思想、方法的理解和掌握，利于拓展学生思维的深度和广度.

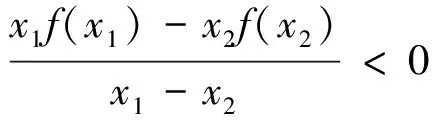
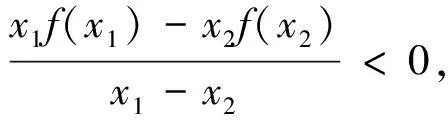
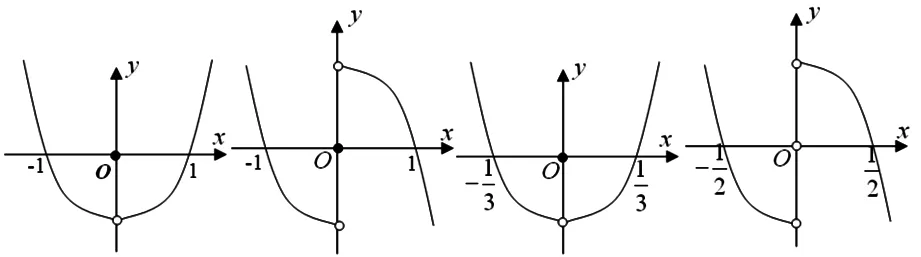
图1 图2 图3 图4

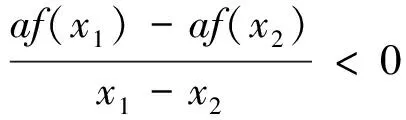
简解:由已知，可得a≠0，y=g(x)=af(x)为R上的奇函数，在(-∞，0)和(0，+∞)上均为减函数，g(-1)=g(1)=g(0)=0，画函数y=g(x)=af(x)草图，如图2，点(0，0)在函数的图像上，得不等式af(x)≤0的解集为(-1，0)∪(1，+∞)，不等式af(x)≤0的解集为[-1，0]∪[1，+∞.

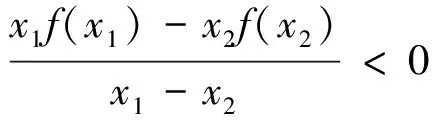
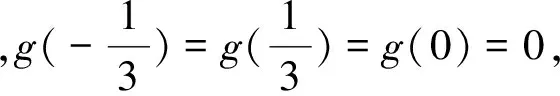
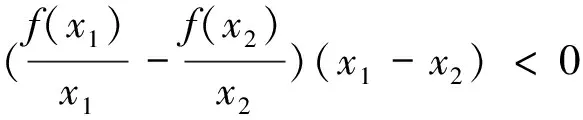
点评:以上四道题，各题本质相同，具有通性，涉及的都是抽象函数问题，综合考查函数的奇偶性、单调性、不等式性质等，都可用“数形结合”思想解决，让抽象的“数”的问题，转化为具体的“形”的问题.

1.2 “一题多变”解题教学的注意点

(1)杜绝教师的直接告知

课堂上，一道变式题目出来之后，要留有足够的时间让学生思考、探究，并且最好让学生先说出解题思路，让学生体会自行解题的成就感，应杜绝缺少学生思考探究的直接告知.

(2)避免变式题过多过滥

进行“一题多变”解题教学时，要避免变式题过多过滥，哪怕只有一、两道变式题，只要讲足讲透，让学生清楚其中所蕴含的思想、方法，有时也是高效的，而变式题目过多的教学后果往往是囫囵吞枣，效果不佳.

2 一题多法

2.1 “一题多法”含义、作用及案例点评

“一题多法”是从不同的角度去分析、解决同一个问题，利于加深学生对基础知识、基本方法的理解，利于培养学生思维的发散性和求异性.

案例2 已知a>0，b>0，ab=a+b+3，求ab的取值范围.

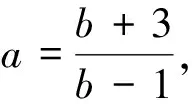
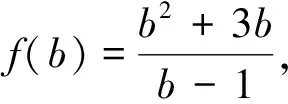
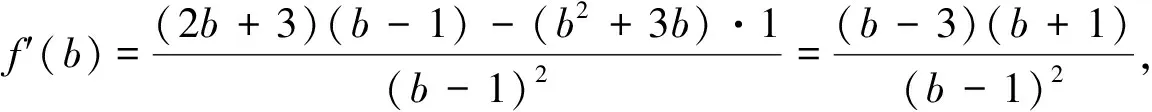
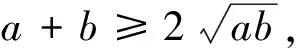
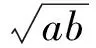
2.2 “一题多法”解题教学的注意点

(1)方法数量适中

课堂教学时，对同一题解法不宜讲解太多，否则，学生会分不清主次，对于有多种解法的题目，课堂上选择2至3种常规性和普适性解法讲解即可.

(2)谨慎选讲“巧解”

对于学生“蹦一蹦，跳一跳”可以理解的巧解可以选讲，但一定不要讲解那些教师“很得意”而学生感觉似“从天而降”的巧解，这些巧解只能让学生惊叹、欣赏，很难学会、领悟，浪费时间.

(3)舍得放弃“繁解”

不能为体现一种解法的巧，而故意挖掘一种繁解，否则，既不利于培养学生的思维能力，也不利于提高学生的解题能力.

(4)解法不能“硬塞”给学生

各种解法不应是由教师“硬塞”给学生，而是应由教师引导学生发现，或由学生完全独立探究而得到，否则，学生会“消化不良”，极易产生“懂而不会”现象.

(5)考试中学会采撷优法

在考试中，对多法题目，要学会在脑海中进行筛选，最终选择哪种方法，要根据自己适应哪种解题思路，对哪种方法理解得更透彻进行选择[1].

(6)根据学情确定是否要“一题多法”

在课堂上，如果学生对于某题，全都会用某种简捷方法解决了，那就没有必要为了“一题多法”，而再要求学生说出别的方法.从认知心理学角度看，找到简便方法后，学生心理缺口已经补好，他心理上满足了，也就丧失进一步探求的动力，这时，你再要求他探究新方法，这是不自然的[2]，也是低效的，浪费时间的.

3 结束语

经常进行“一题多变”和“一题多法”的解题训练，利于学生“跳出题海”，达到事半功倍的教学效果，确保学生再遇类似题目时能将方法顺利迁移，消除“懂而不会”现象，实现有效教学；利于优化学生的思维的深刻性、敏捷性、发散性、求异性等品质，对学生终身发展都有积极的影响，实现数学教育教学的长期有效性.

[1]王 千.如何认识一题多解的教育功能[J].数学通报，2004(9)：10-12.

[2]刘鸿春.追求自然 唤醒认知—“数学归纳法”的教学设计与思考[J].中小学数学，2014(11)：27-29.

江苏省中小学教学研究第十一期重点课题《数学有效教学行为的研究——数学学习中懂而不会现象的研究》的阶段性成果，课题编号：2015JK11-Z024.