留白 游戏 享受
——高中数学课堂追求本真、灵动三例
江苏省常熟市中学 (215500) 吴旭红
留白 游戏 享受
——高中数学课堂追求本真、灵动三例
江苏省常熟市中学 (215500) 吴旭红
2016年6月16日参加了常熟市中学数学特级教师工作室2016年第三次活动,聆听了苏州市教育科学研究院吴锷主任的《构建本真灵动的苏式数学课堂》,对于数学课堂的本真——本质是什么?核心是什么?思维是什么?思维方式是什么?思维品质到思维品格的提升需要灵动的生命气象,让研究成为一种常态,让课堂成为学生为主体,师生共同的舞台,让每个学生可以自由思想,独立思考,勇敢尝试,迸发出生命的智慧潜能,体验生命成长的幸福感觉等有了更深的认识.
本文通过三节课简录或部分片段,展示教师如何设计实施来体会高中数学课堂的本真与灵动.
一、留白显创造,归纳是本质,感悟在探究
案例一 (高一)浒浦中学高一(8)班借班上课(常熟市中学沈宏《数列通项公式的求法》2016.6.16)
引入:裴波拉契数列引出数列递推公式的概念,指出数列重点研究递推关系,数列的通项是数列学习的核心问题.
温故知新1 已知数列{an}中,a1=1,an+1=an+2,则an= .
生集体回答结果,某生具体回答思维过程,复习了等差数列定义、通项公式的求解方法(叠加法),n=1的检验,教师引导学生观察可以这么做的原因(右边可以求和),问怎样的式子可以求和呢?请同学们创造可以求和的题,并自行解决.
已知数列{an}中,a1=1, ,则an= .
学生开始创造.本人坐在两列中间,周围有四个同学,左边两位女生,右边两位男生(下文记为左1左2右1右2).创造如下.左1:an+1+2=an+4,右1:an+1-an=2n-1,右2:an-an-1=n,左2好不容易写了个Sn=2n-1,却没有做下去,作为听课老师我觉得她出的也不错,跟左1类似.可见部分学生对于常数可以求和,等差数列印象深刻,部分学生已经学会变通.
教师投影的是位女生甲的作品:an+1-an=2n.教师跟学生一起检查书写过程,要求大家检验n=1规范完整,引导学生感悟归纳出an+1-an=f(n)型(可求和),可用叠加法,友情提示——验证首项.
温故知新2 已知数列{an}中,a1=1,an+1=2an,则an= .
同法处理本问题.教师引导学生观察出原理——相乘可以上下相消,请学生构造,提醒学生重视乘积可求或者平时作业中遇到怎样的问题可以用这个来求解.
已知数列{an}中,a1=1, ,则an= .

思维拓展探究1:已知数列{an}中,a1=1,an+1=2an+2,求an.
教师引导学生分析猜测可能是什么数列?怎么创造条件,学生乙回答,师板书.归纳an+1=pan+c型,适用待定系数法.

学生探究.左1左2右1右2四位同学皆直接取倒数,构造得出.说明学生掌握得很好.

本题取倒数与构造(待定系数法)相结合.左1左2右1右2四位同学皆正确完成.
探究3 已知数列{an}中,a1=1,Sn=2an-1,求an.

思考题:已知数列{an}中,a1=3,an+1=2Sn,求an.
左1左2同学皆用Sn+1-Sn=2Sn,先证{Sn}为等比数列,再求解an,皆为分段形式.右1由an+1=3an,a1=3≠0,得{an}为等比数列,右2类似,投影的同学丁亦是如此,说明学生仅记忆了要检验n=1,却不重视条件对式子的约束.教师的分析到位,之后总结本节收获,求解数列通项公式的常见方法.
点评:诗云“如切如磋,如琢如磨”,沈宏老师通过“切”——温故知新,思考初始情境,学生既复习了基础知识,又理解了其适用的内涵;“磋”——探究新知,大胆留白,鼓励创造,激活了学生头脑中已有旧知,进行意义建构,在思维的锻炼中提高能力;“琢”——思维拓展,逐步深入,放手学生构建新数列,学生凭直觉获得宝贵经验,并由表及里,深入理解后解决了取倒数和构造两者结合的思考题.“磨”——精雕细刻在细微处,沈宏老师根据教学经验,结合课堂实际,抓住学生在数列学习中对n=1,n≥2等认识上的不足,给出思考题,大胆留给学生处理,让学生出错,并在探究3的基础上,引领学生逐步理解递推含义,及检验的本质——完备性.
二、游戏进课堂,数学映生活,本真引思想
案例二 (高二)2016年4月26日,启发深度思考,实践深度教学——常熟市中学数学 “双主课堂”教学研讨活动(江苏省常熟中学朱峰《基本不等式》)


朱峰老师后来介绍了他设计游戏引入法的原因:通过对教材的分析,感觉无论天平称重还是弦图,调价或者用不等式a2+b2≥2ab类比引入,皆感觉学生不好进入角色,后受“女儿跟同学猜拳赢蚕宝宝”的启发,结合纸牌这个大家都喜欢的工具,设计了纸牌游戏法.
江苏省教育厅教研室李善良博士点评:本课有四个难点——引入,猜想(成立条件),证明,几何解释,还有各种变式应用.朱峰老师情景创设有趣简单,猜想结果一定是教师引导,学生归纳出抽象结果,证明方法多,通过这堂课学习,学生对原结构印象深刻,结构变式就强化这个基础.教师的任务就是教会学生用数学的眼光观察世界,用数学的思维思考世界,用数学的语言表达世界,关注数学本质的揭示,与学生的思维相匹配.
本节课给了“我们要培养学生发现问题,提出问题的能力”一个很好地示范,学生主体得到了充分的体现,增加了基本经验的积累,智慧逐步生成,师生充满激情,与实际生活很好地链接在一起.通过学生的直观感受,观察发现,理解顿悟,深入认识.课堂上有疑问,有猜想,有笑声.通过体验生活,让每一个学生都成为实践者.
三、学生为主体,配角作引导,自主即享受
案例三 (高三)南京二模试卷讲评课片段(常熟市中学高三(10)班 本人2016.4.15)

高三的三轮复习中,有时候,学生做的试卷中一些题目正确率很高,也许有的老师认为学生掌握得不错,没有再评讲的必要了,但是实际上可以平淡中见神奇,以这些题目为例,复习基础知识,基本技能,方法选择,甚至简化,变化,进行思维训练,让学生相互交流,互相评价,让每一位学生仍有所获.阅卷过程发现学生本题完成得很好,仅3位同学出现了计算错误.即使正确率很高,结合之前学生的复习状况,学生题目边上留下的做题痕迹,加之向量兼具数与形的特征,也是知识交汇点,本人仍觉得很有探究一番的必要.
课堂开始,师表扬大家前10题做得很好,11题仅三位同学出错(错误学生开始自己订正),首先我们请张译夫同学上台给大家介绍他的求解方法(该生以前此类问题常错,并且喜欢表现,即通常说的常需鼓励,肯定).
他在台上自信地说:我是用基底表示的,我给大家分析一下:

师:嗯,张同学的方法怎样?
生:挺常规的,两个向量夹角知道,一边知道,只是要用到解方程.
师:对,比平时的题稍难一点,但是按常规方法处理也是可行的.那么你还会用什么方法来处理呢?
徐露同学:坐标法.师:请徐露同学给大家看看她的想法.

师:徐露的方法你想到了吗?(很多学生附和),没想到这么做的同学是否已经思考求解了一遍呢?
张文钧同学提出了不同的意见:老师,把C放在x轴正半轴上,B点坐标是明确的,根据向量相等的关系,也可以求出D点的坐标啊.
师:大家说呢?生:倒也是,反正都是求点的坐标,本质是一样的.

桂裕华同学:老师,直接用余弦定理就好了!

图1
师:桂同学什么意思呢?有请桂同学给大家展示.
桂裕华龙飞凤舞的字瞬间就出现在黑板上,而且写得超简洁.

大家:哦!我也这么做的,桂哥强!
师:嗯,不错.抓住角互补,余弦值相反,设了两个变量,解方程,基本功不错,不愧为课代表!大家要向他学习,认真解方程啊!
大家笑了,马上有学生提醒:老师,海波还有妙法!原来学生正相互积极地探讨着呢!
师:大家欢迎陶海波同学!
学生鼓掌欢迎,倒把大个的海波同学弄得有点不好意思了.
陶海波同学:我倒是既没有基底法,也没用建标法,解三角形我觉得烦,然后根据向量关系,我发现很多边可以直接求出来,大家看看好不好?

图2

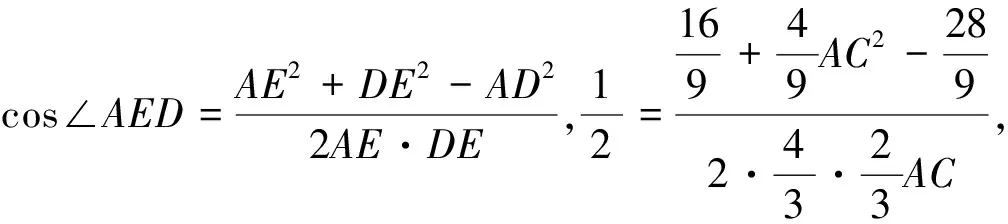
师:大家说好不好?生集体回答好!师问,不妨也起个名字?生:几何法!师竖起了大拇指.
海波同学开心的走下去了,平时做题一丝不苟的男生唐若诚说:“老师,我的也是几何法,不过跟海波不一样”.于是我们聆听了唐同学的思路,他给大家投影了他的做法.

图3


师:大家讲得都不错,向量问题的常规思路大家掌握得很好了,它的数形特征让我们入手方法多样,牵涉的知识公式也多,希望大家以后碰到向量题大胆地向它进攻,选择最好的你最喜欢的方法,迅速准确地解出来.大家要在课后做好整理.子曰:“学而时习之,不亦说乎?”同学们经常归纳整理,“联点成线,联线成面,最终归为一点”,要有自我建构数学知识的意识.(课后,让课上回答的同学把各自方法,张贴于教室,供大家参考欣赏)
自评:高三的三轮复习,似乎学生都会了,又似乎学生什么都忘了,课堂往往是试卷的评讲,那么讲得精彩,讲清关键点,谁讲?怎么激发学生以及教师自己的热情?教会学生对数学思想方法的娴熟使用?怎样提高运算求简能力,达到高效解题?本人认为要重基础,抓主干,悟规律,求实效.把课堂还给学生,本人觉得学生讲比较能激励学生,让学生能够有表现自己的机会,与同学分享自己的成果,让大家进行比较,享受数学的奇妙.教师仅需创造良好的环境氛围,适当穿针引线,提高学生的参与度,思维广度,激发学生的自主性,创造性.更可以通过拓展,变式,提高阅读,分析计算能力,注重养成教育,培养习惯,形成规范,培养学生良好的心理素质,发展学生的思维能力,布鲁诺说:发现学习,探究学习,再发现,再创造.学生通过不同角度分析、解决问题,围绕一个数学问题复习多块知识,多种思想方法,促使学生根据自己的认知基础和思维特点进行选择,探索去解决问题的有效方法.

教学的根本目的在于丰富学生的知识,发展学生的数学思维,提高学生的数学素养,培养学生的理性精神,让学生学会发现问题本质,学会分析,解决问题,在此过程中掌握思考,感悟问题解决的数学思想与数学方法.李善良博士提倡:把精彩留给学生,凡学生能做的留给学生.
用吴锷主任对苏式课堂教学的核心“立本求真”作为本文的结束语:遵循教学规律,从学生认知特点出发,顺应学生思想意识,通过数学活动,获得经验积累,自我构建数学知识,拓展空间,让探究成为习惯,让学生享受数学.

