一道高中联赛题的探究及其一般化*

●梁昌金 (寿县第一中学 安徽寿县 232200)

一道高中联赛题的探究及其一般化*

●梁昌金 (寿县第一中学 安徽寿县 232200)

文章给出2016年全国高中数学联赛辽宁赛区预选赛第13题的4种证明，然后对结论作了类比，获得3个新命题，最后对获得的结论进行了一般化的探究，通过合理的证明，进而得到更完美的结论.

高中联赛；几何不等式；类比探究；一般化

题目 如图1所示，△ABC为锐角三角形，外接圆圆心为O，半径为R，AO的延长线交△BOC的外接圆于点A′，BO的延长线交△AOC的外接圆于点B′，CO的延长线交△AOB的外接圆于点C′，求证：OA′·OB′·OC′≥8R3.

(2016年全国高中数学联赛辽宁赛区预选赛试题第13题)

试题图形简洁优美，激发了笔者的探究欲望.从不同的角度运用图形特征，建立相关量之间的联系，可以得到不同的证明方法.

1 证法探究

以下证法1～证法3是对结论的一种等价性变换代数化证明[1]，证法4是通过添加辅助线，利用三角法的直接证明.

证法1 如图2所示，设AO,BO,CO分别交对边BC,CA,AB于点D,E,F.由点B,O,C,A′共圆，知

∠OBD=∠OCB=∠OA′B,

从而

△OBD∽△OA′B，

于是

即

同理可得

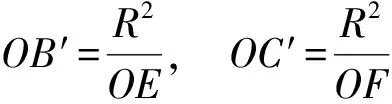
因此

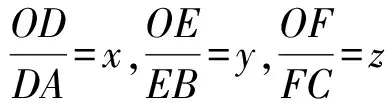
x+y+z=1.

同理可得

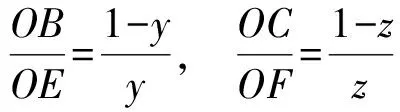
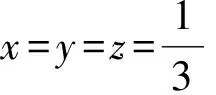
OA′·OB′·OC′≥8R3，

当且仅当△ABC为等边三角形时等号成立.

证法2 如图2所示，设AO,BO,CO分别交对边BC,CA,AB于点D,E,F，△OBC，△OCA,△OAB的面积依次为x，y，z,则

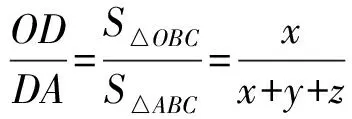
从而

同理可得

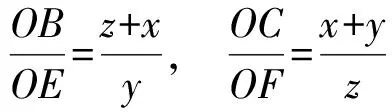
同证法1可得

当且仅当x=y=z时等号成立，此时△ABC为等边三角形.故OA′·OB′·OC′≥8R3，当且仅当△ABC为等边三角形时等号成立.

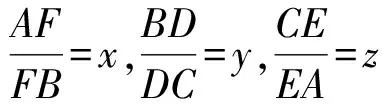
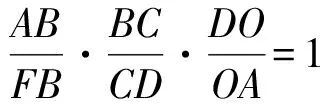
从而

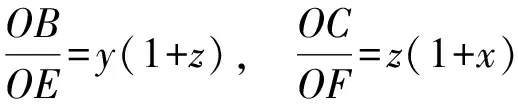
同证法1可得

x(1+y)·y(1+z)·z(1+x)=

xyz(1+x)(1+y)(1+z)≥

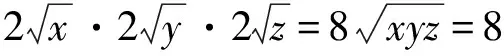
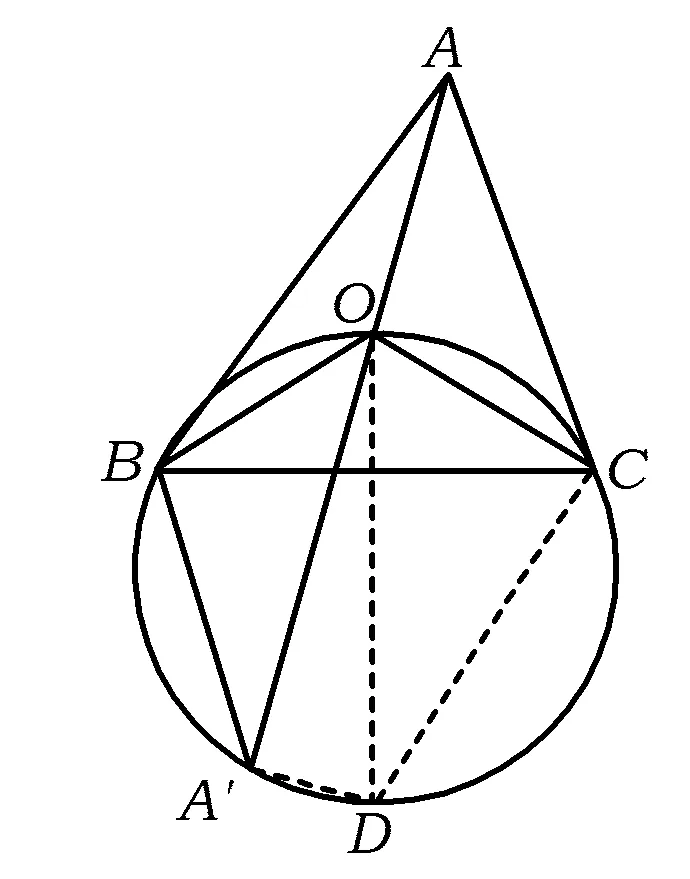
图3

当且仅当x=y=z时等号成立，此时△ABC为等边三角形.于是

OA′·OB′·OC′≥8R3，

当且仅当为△ABC等边三角形时等号成立.

证法4 如图3所示，作△BOC外接圆的直径OD，联结A′D，CD，则

∠OA′D=∠OCD=90°,

从而

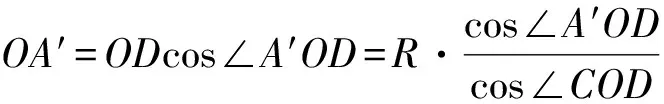
又易知OD⊥BC，得

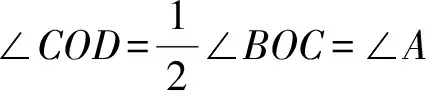
从而 ∠A′OD= 180°-∠COD-∠COA=

180°-∠A-2∠B=

∠C-∠B,

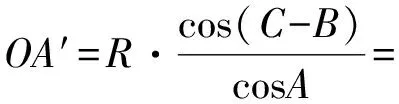
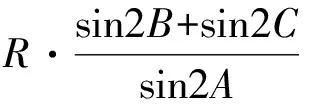
同理可得

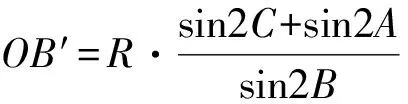
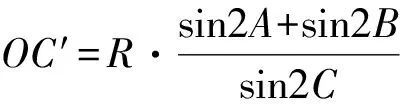
sin2A>0, sin2B>0, sin2C>0,

于是，由均值不等式得

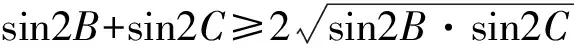
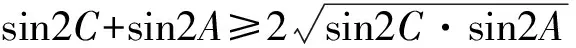
以上3个式子相乘得

(sin2A+sin2B)(sin2B+sin2C)(sin2C+sin2A)≥

8sin2A·sin2B·sin2C,

当且仅当A=B=C时等号成立，此时△ABC为等边三角形.故

OA′·OB′·OC′≥8R3，

当且仅当△ABC为等边三角形时等号成立.

2 类比探究

类比是一个伟大的引路人.联赛题给出了锐角三角形外心的一个优美几何不等式，若将外心O替换成△ABC的垂心H、内心I、重心G，是否具有相似的结论呢[2]？答案是肯定的，以下笔者给出垂心时的证明，限于篇幅，内心、重心相关结论的证明不再赘述，留给有兴趣的读者探究.

命题1 若点H为锐角△ABC的垂心，AH的延长线交△BHC的外接圆于点A′，BH的延长线交△AHC的外接圆于点B′，CH的延长线交△AHB的外接圆于点C′，则

HA′·HB′·HC′≥8HA·HB·HC.

命题2 若点I为锐角△ABC的内心，AI的延长线交△BIC的外接圆于点A′，BI的延长线交△AIC的外接圆于点B′，CI的延长线交△AIB的外接圆于点C′，则

IA′·IB′·IC′≥8IA·IB·IC.

命题3 若点G为锐角△ABC的重心，AG的延长线交△BGC的外接圆于点A′，BG的延长线交△AGC的外接圆于点B′，CG的延长线交△AGB的外接圆于点C′，则

GA′·GB′·GC′≥8GA·GB·GC.

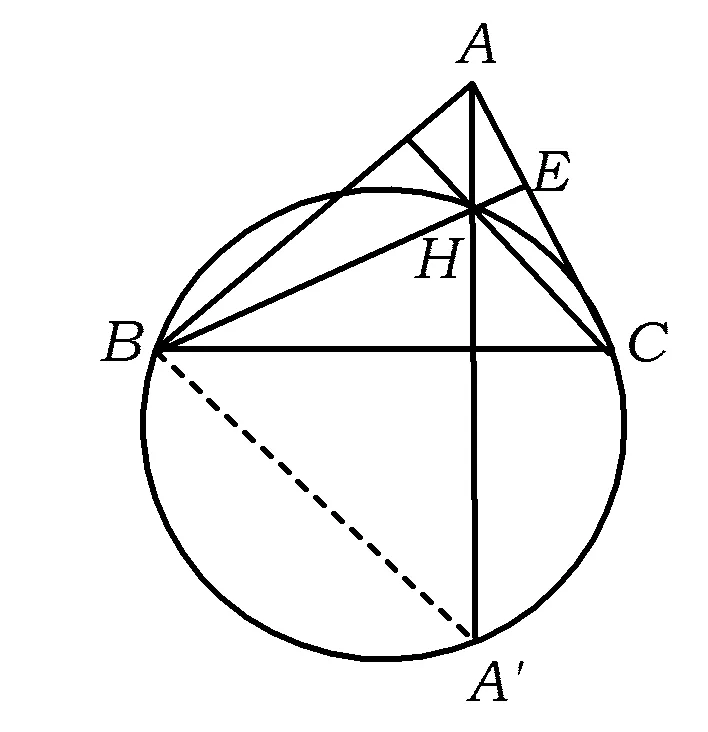
图4

命题1的证明 记△ABC的外接圆半径为R.如图4所示，设BH与AC相交于点E.

在Rt△AEH中,

2RcosA,

同理可得HB=2RcosB，HC=2RcosC.

在△A′BH中，易知

从而 ∠A′BH= ∠A′BC+∠CBH=

∠A′HC+∠CBH=

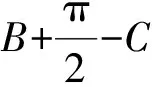
在△A′BH中，由正弦定理得

从而

HA′=2Rcos(B-C),

同理可得HB′=2Rcos(C-A),

HC′=2Rcos(A-B).

于是

同理可得

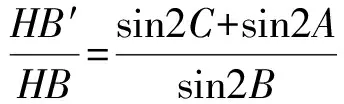
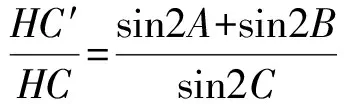
因此

HA′·HB′·HC′≥8HA·HB·HC，

当且仅当△ABC为等边三角形时等号成立.

3 一般化的结论

上述联赛题和3个命题给出了三角形4个特殊点的一种统一结论.一个自然的想法是:若将外心O、垂心H、内心I、重心G一般化为锐角△ABC内任意一点P，是否具有相似的结论？即PA′·PB′·PC′≥8PA·PB·PC是否成立[3]？答案是肯定的.

命题4 若点P为锐角△ABC内任意一点，AP的延长线交△BPC的外接圆于点A′，BP的延长线交△APC的外接圆于点B′，CP的延长线交△APB的外接圆于点C′，则

PA′·PB′·PC′≥8PA·PB·PC.

图5

证明 如图5所示，设∠BPA′=α,∠CPA′=β,∠CPB′=γ,由托勒密定理知

PA′·BC=PB·A′C+PC·A′B.

在△A′BC中，应用正弦定理得

从而

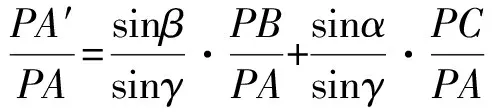
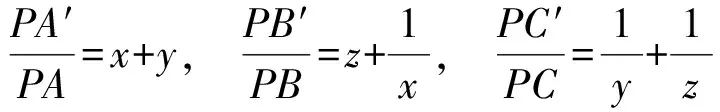
于是

PA′·PB′·PC′≥8PA·PB·PC.

[1] 梁昌金.一类几何竞赛题的代数化证明[J].数学通讯：下半月，2015(12):57-59.

[2] 梁昌金.第2130号数学问题的简证及其类比[J].数学通讯：下半月，2016(4):63-65.

[3] 梁昌金.2道数学竞赛题的证明[J].中学教研(数学)，2016(6):48-封底.

��2016-10-21；

2016-11-25

梁昌金(1981-)，男，安徽寿县人，中学一级教师.研究方向：数学教育.

O123.1

A

1003-6407(2017)03-48-03