例谈2个动点间距离最值问题的几种解题途径*

●杨伟达 (花都区第二中学 广东广州 510820)

例谈2个动点间距离最值问题的几种解题途径*

●杨伟达 (花都区第二中学 广东广州 510820)

有关距离的最值问题在中学数学中占有举足轻重的地位，在全国各地的高考试题中也频频出现.它呈现出变化多、涉及面广、形式灵活的特点，分值影响着数学高考的难度，其出现常常成为数学高考难度的“风向标”.

动点;距离;最值;解题途径

众所周知，距离问题本是一个古老的话题[1].但在每年的高考中，它常常成为专家命题的第一视角，是许多学生在数学考试中的绊脚石.因此，在解题中若能处理好有关距离的最值问题，则将对快速解题产生事半功倍的效果.下面是笔者从不同角度对2个动点间距离最值问题进行析疑解惑，凸显“动”的魅力，焕发出“新”的活力.

1 借助特殊曲线，寻求等价替换

有这样的一类题：2个动点分别在常见的特殊曲线上，且该特殊曲线具有特殊的性质.此时可以通过观察图形，利用图形的特殊性质求得最值.

例1 已知⊙C的方程：x2+y2+2x-4y+3=0.

1)略;

2)从⊙C外一点P(x,y)向圆引一条切线，M为切点，O为坐标原点，且|PM|=|PO|，求使|PM|最小的点P坐标.

分析 一个动点在圆外，另一个在圆上，且这2个动点的连线恰好是圆的切线(特殊).解决此题的关键在于利用圆的特殊性质，找到切线长作为等价替换，问题即可解决.

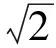
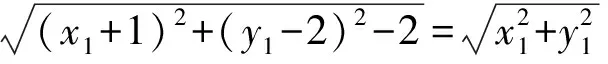
化简得2x1-4y1+3=0(这就是点P满足的轨迹方程).

因为|PM|=|PO|，所以|PM|的最小值就是|PO|的最小值.而|PO|的最小值可转化为原点到直线2x1-4y1+3=0的距离，即

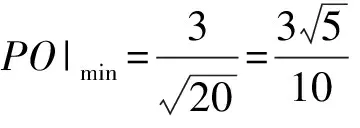
联立方程组

解得

( )

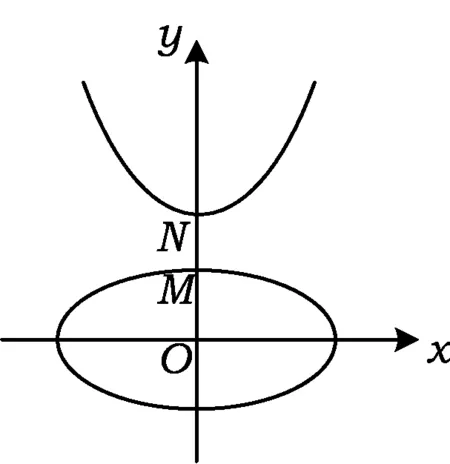
图1

分析 如图1，画出草图，不难发现2条曲线相离，且位置比较特殊.观察可知，曲线上2个动点的最短距离转化为2个顶点(定点)间的距离，此时问题就变得简单了.

解 因为M,N间距离的最小值是5,所以椭圆与抛物线不相交.

如图1，此时抛物线的顶点与椭圆上顶点的距离就是动点M,N之间距离的最小值.抛物线的顶点N(0,2m2)，椭圆的顶点M(0,3)，从而动点M,N之间距离的最小值为5,于是

2m2-3=5,

解得m=±2.故选B.

2 借助三角函数，寻求合二为一

1)将曲线C和直线l化为直角坐标方程;

2)设点Q是曲线C上的一个动点，求它到直线l距离的最大值.

(2016年广东省广州市第二次数学测验理科试题第23题)

分析 此类型题在数学高考全国卷的选做题中常常出现.比较快捷的解决方法是利用参数方程表示曲线上的某一动点坐标，再根据条件转化为求三角函数的最值问题.

3 借助数形结合，凸显直观形象

有这样的一类题：它们的一个动点在某区域内，另一个动点在某特殊曲线上.此时2个动点间的距离问题可转化为一个定点到区域内某一动点的距离最值问题.

( )

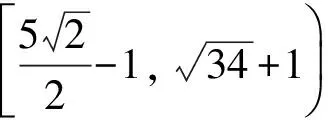
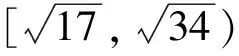
分析 此题涉及线性规划问题.先将不等式组表示成平面区域，再根据圆的特殊性质,通过数形结合可解决问题.

图2

解 由题意：平面区域D表示△ABO(含边缘)的阴影部分，且A(0，3)，O(0，0)，B(1，1)；圆心C的坐标为(5，0)，半径为1(如图2所示).要求2个动点间的距离，可转化为求定点到动点的距离,即先求圆心C到△ABO的阴影部分内任一动点的距离.经观察可知，BC距离为最小,AC距离为最大,于是

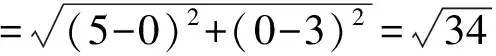
4 借助二次函数，寻求配方到位

有这样的一类题：2个动点分别在常见的特殊曲线上，且这些动点均可以用含参坐标表示.此时可以直接运用距离公式，把它转化为一元二次函数然后求得最值.

例5 如图3，以正方体的3条棱所在直线为坐标轴建立空间直角坐标系O-xyz，点P在正方体的对角线AB上，点Q在正方体的棱CD上.当点P在对角线AB上运动，点Q在棱CD上运动时，探究|PQ|的最小值.

(人教版《数学(选修2-1)》第113页习题B组的

第2题)

图3

分析 这是一道课本习题.2个动点分别在2条异面直线上，关键是把动点用含参坐标表示出来，再转化为一元二次函数求最值.

解 设正方体的边长为a.点P在对角线AB上运动，从而可设P(λ,λ,a-λ)(其中0≤λ≤a).又点Q在棱CD上运动，从而可设Q(0,a,μ)(其中0≤μ≤a),于是

|PQ|2= (0-λ)2+(a-λ)2+(μ-a+λ)2=

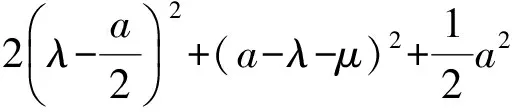
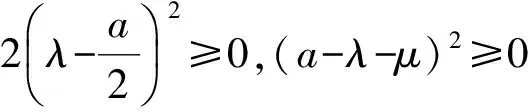
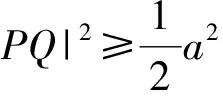
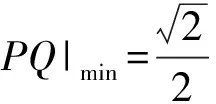
5 借助导数工具，寻求转换条件

有这样的一类题:它们的一动点在一个函数图像上，另一动点在另一个函数(分段函数)图像上.若运用两点间距离公式，则方法简单，但运算复杂，只能可望而不可及；此时若能借助导数这一工具，利用切线间的距离，则比较容易求得最值.

( )

分析 此题涉及到2个函数图像上的2个动点问题，关键在于分别求出2条曲线上切线的最值，此时2条切线互相平行.此类问题要注意进行检验，防止“多一个”或“漏一个”.

解得a=2.

图4

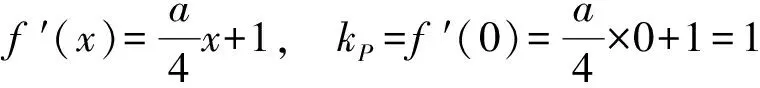
[1] 杨伟达.浅谈解析几何中几种常见的最值问题[J].中学生数学，2014(7)：15-16.

��2016-09-14；

2016-10-28

杨伟达(1973-)，男，广东广州，中学一级教师.研究方向：数学教育.

O123.1

A

1003-6407(2017)03-06-03