一道高考试题的探源及推论的应用

北京市陈经纶中学 (100020) 张留杰江西省萍乡中学 (337055) 黄贤锋

一道高考试题的探源及推论的应用

北京市陈经纶中学 (100020) 张留杰江西省萍乡中学 (337055) 黄贤锋

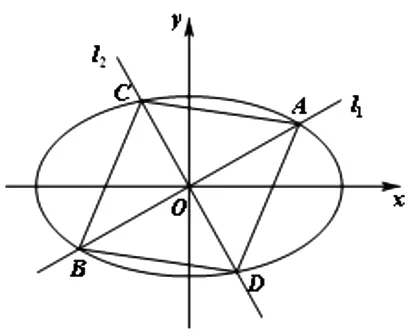
图1

题目 (2015年上海高考数学第21题)已知椭圆x2+2y2=1，过原点的两条直线l1和l2分别于椭圆交于A、B和C、D，记得到的平行四边形ABCD的面积为S(如图1)．

(1)设A(x1,y1)，C(x2,y2)，用A、C的坐标表示点C到直线l1的距离，并证明S=2|x1y2-x2y1|；

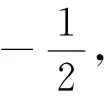
一、试题的根源探究

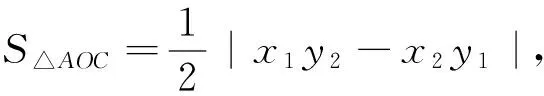
此高考题让笔者联想到北师大版高中数学教材《必修5》第48页例3，也正是本题的题根所在．我们不妨把它作为本文的定理．

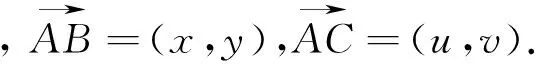
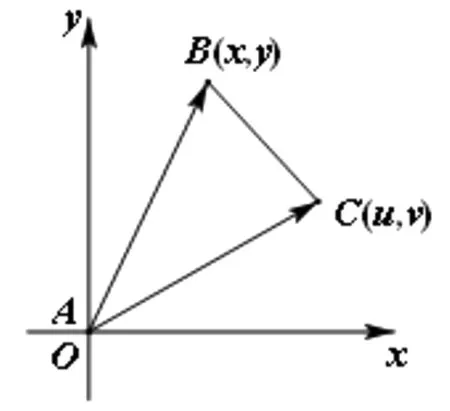
图2

证明：如图2，以点A为坐标原点，建立平面直角坐标系，

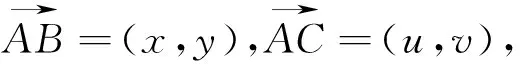
我们可以称该公式为三角形面积公式的向量形式(坐标形式)，它和三角形面积的行列式形式也是一致的．

能否根据上述三角形面积公式求解任意四边形的面积呢？经过探究，得出如下推论．

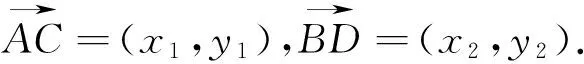
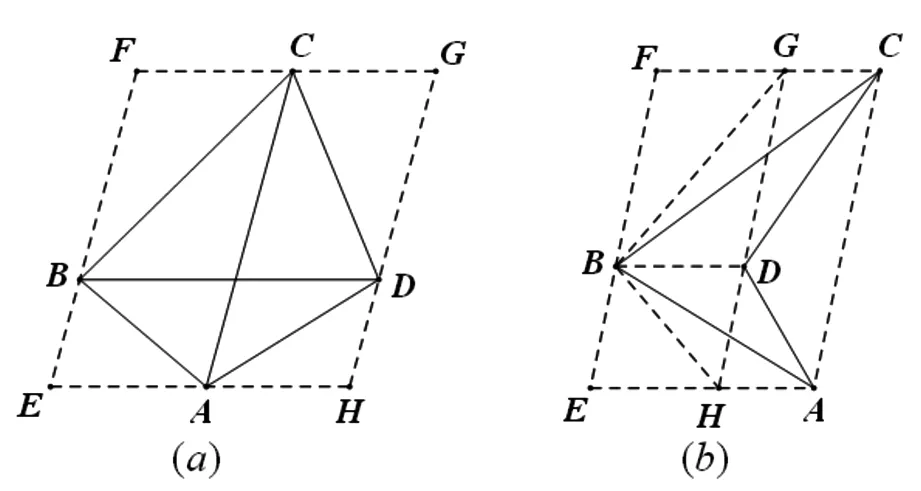
图3

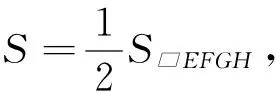
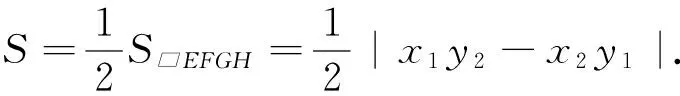
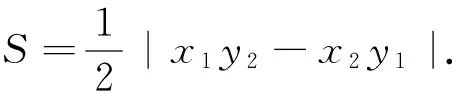
二、推论的应用举例

本文的推论为解决圆锥曲线中四边形面积问题提供了一种有力的工具，下面结合两道高考真题谈谈它的应用．

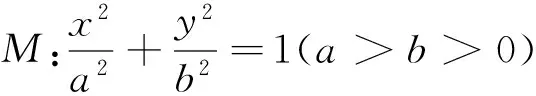
(1)求椭圆M的方程；

(2)C，D为M上的两点，若四边形ACBD的对角线CD⊥AB，求四边形ACBD面积的最大值．

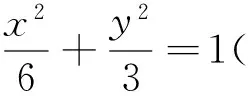
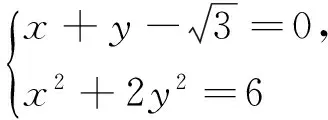
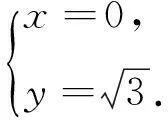
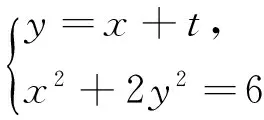
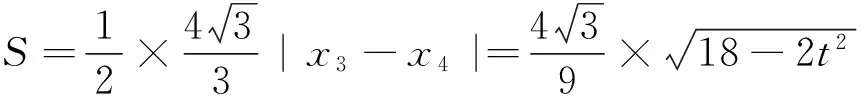
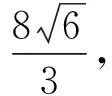
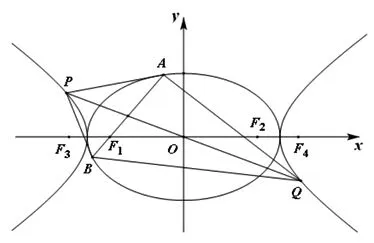
图4

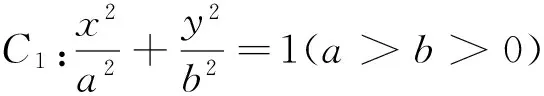
(1)求C1，C2的方程；

(2)过F1作C1的不垂直于y轴的弦AB，M为AB的中点．当直线OM与C2交于P，Q两点时，求四边形APBQ面积的最小值．

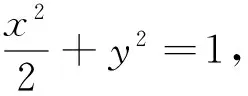
(2)设A(x1,y1)，B(x2,y2)，P(x3,y3)，Q(-x3,

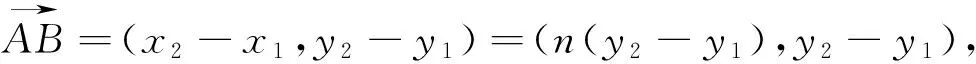
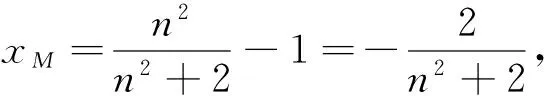
所以当n=0时，Smin=2．故四边形APBQ面积的最小值为2．