变“瑕不掩瑜”为“金镶玉”
江苏省江阴市华士高级中学 (214421) 费振东
变“瑕不掩瑜”为“金镶玉”
江苏省江阴市华士高级中学 (214421) 费振东
在高中数学教学的各个环节中,时常会涌现出一些预设之外的错误,有的错误会被我们一带而过,有的错误则反复在学生的作业或考试中“借题发挥”,成为“玉上的瑕疵”. 对那些一而再的错误,我们通常会指责学生“榆木”脑袋,很少向内归因:是否我们的教学设计或教学组织出了问题?能否把以前学生出现过的错误和现在学生在探究过程中出现的错误作为课程资源,加以开发利用呢?让“错误的瑕疵”成为整体教学上的点缀,变“瑕不掩瑜”为“金镶玉” ,变“错误”为“悟错”,科学而艺术的变缺为好,实现教学中的民主互动,促进高中生的深度学习.为此,我用了近三年的时间,对这一课题进行教学试验,取得了很好的教学效果,现总结如下,以期抛砖引玉.
一、利用错误,激发探讨兴趣
在每节新课开始,我都会设置一个典型的案例,这个案例可能是前面作业中的典型错误,也可能是引入新课题时的材料分析中故意设计的错误,利用学生天性中的纠错因子,激发学生探究的兴趣.这些材料来自于学生,贴近学生,通过辨析,既强化了已学概念和规律的理解,又为学习新知识做好了必要的铺垫.
教学案例一 过点(0,1)且与抛物线y2=2x仅有一个交点的直线方程是 .
错因分析:此处解法易犯三处错误:
第一,设所求直线为y=kx+1时,没有考虑k=0与斜率不存在的情形,实际上就是承认了该直线的斜率是存在的,且不为零,这是不严密的.
第二,题中要求直线与抛物线只有一个交点,它包含相交和相切两种情况,而上述解法没有考虑相切的情况,只考虑相交的情况.原因是对于直线与抛物线“相切”和“只有一个交点”的关系理解不透.
第三,将直线方程与抛物线方程联立后得一个一元二次方程,要考虑它的判别式,所以它的二次项系数不能为零,即k≠0,而上述解法没作考虑,表现出思维不严密.
正确答案:①当所求直线斜率不存在时,即直线垂直x轴,因为过点(0,1),所以x=0,即y轴,它正好与抛物线y2=2x相切.
②当所求直线斜率为零时,直线为y= 1平行x轴,它正好与抛物线y2=2x只有一个交点.

分析与反思:每一个错误的背后,都应隐藏着思维的缺陷:有的是基础知识理解不清,感知粗略,不精细;有的是思维定势,不发散;有的是注意失调,不集中;有的是记忆还原,不深刻.如何开发和利用好学生自身的错误资源,用错误来取得突破,是复习巩固的最好策略.
二、利用错误,激活创新思维
在新课学习时,学生头脑中的前科学概念中有很多错误的观点或认识,如果不让这些观点或认识得到纠正和完善,肯定会影响重要知识点的学习质量,这时就需要老师通过“设疑自探——解疑合探——质疑再探”,使学习过程中认识上的错误得以充分暴露,适时、适度地给予点拨和鼓励,能帮助学生突破眼前的思维障碍,进入创新求异的新境界,让学生体验到思维的价值,享受到思维的快乐.
教学案例二 设数列的前n项和为Sn=n2+2n+4,求这个数列的通项公式.
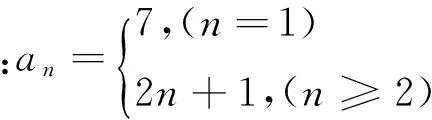
错因分析:易缺失n=1的情况,以偏概全,误认为任何情况下都有an=Sn-Sn-1.
分析与反思:学生犯错误的过程,其实正是不断改正错误,完善方法的过程.对学生学习来说,所有的错误都可以转化为尝试后找到新的出发点,他们需要从错误中产生动力的能力,并且能从中找到一些有价值的东西.
三、利用错误,调整教学方案
在对难点学习的组织中,课堂教学充满着许多变数,也会出现诸多错误.有的错误具有比较高的生成价值,有效利用,将错就错,及时调整教学设计,就可以创造教学精彩.

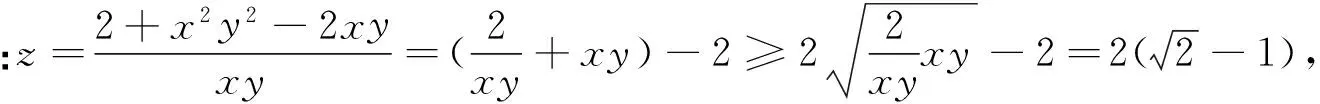

分析与反思:在这道题目上我放手让学生去做,让他们从错中反思,错的明白.有效教学的鼓锤敲在学生发展的需要和愿望的鼓点上,才能奏响动听的旋律,这时候需要切记:该出手时才出手!出手的“手段”要缓一些,不牵着学生思维走,多用眼神期待学生;出手的“手法”要放一些,不直接给出他们急于想得到的答案,多用话语激励;出手的“手气”要柔一些,不碰伤学生的心灵,尊重学生.尤其是那些学困生,需要花更长的时间去苦苦思索,记住给他们时间,不要急于把那些本来可以自行调整的事情看作问题.
四、利用错误,提高反思能力.
在作业设计中,根据以前学生暴露的错误,适当地布置一些“陷阱”题,进一步促进学生充分认识错误、认识自己,达到“吃一堑长一智”的目的.
教学案例四 已知数列{an}中,an=n2-kn(n∈N*),且{an}单调递增,则k的取值范围是________.正确答案:(-∞,3).

在渡槽通水运行不卸荷加固条件下,渡槽碳纤维贴片加固后槽身裂缝得到抑制,且具有投资少,效果好,有效解决了实际工程问题,值得借鉴。
正确解析:由于an+1-an=(n+1)2-k(n+1)-n2+kn=2n+1-k,且{an}单调递增,故有an+1-an>0,即2n+1-k>0恒成立,分离变量得k<2n+1,所以k<3.
分析与反思:基础好的学生在解答时很容易用二次函数的性质解题,忽略其定义域为正整数集从而出现错误.这个阶段的错误往往只是因为他们掉进了自己设置的思维陷阱里,我们要做的是通过交流,引起学生重新思考,让他们通过自己的努力从思维陷阱里走出来,从而在他们的方法论体系中种下发展的种子,明白“欲速则不达”的道理,注意区别形似质异题.
五、利用错误,培养质疑意识
在习题分析或试题讲评的教学设计中,故意设置一些以前学生出现的“错误”,让学生顺着错误的思维,最终得出错误的结论或矛盾的结果,再反过来让学生反思错误所在,既培养学生不迷信老师的质疑精神,又让学生有自我展示的成就感.
教学案例五 设f(x)=ax2+bx,且1≤f(-1)≤2,2≤f(1)≤4,求f(-2)的取值范围.
错因分析:此题极易由已知二不等式求出a、b的范围,然后再求4a-2b即f(-2)的范围,这种解法错在已知二不等式中的等号成立的条件不一定相同,它们表示的区域也不一定相同,用待定系数法则容易避免上述错误.
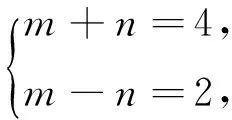
∴f(-2)=3f(-1)+f(1),∵1≤f(-1)<2,2≤f(1)≤4,∴5≤3f(-1)+f(1)≤10,即5≤f(-2)≤10.
分析与反思:IBM创始人华特说过一句或许有点极端的话:“成功的法则就是把犯错的速度提高一倍.”在教学中,巧妙地人为制造“错误”,以“错”引知,以“错”强知,能起到比常规教学更好的教学效果.
回顾课堂教学,以前总是好心地为学生斩断了无数荆棘,给学生架设平坦的学习空间,本身便是一种“低级错误”, 教学设计的这种思维惯性,不仅使老师自身产生了“路径依赖”,而且使学生的问题解决也产生了“路径依赖”,依赖的结果,是老师的外部强化和学生的自发探索的“临界点”无法被有效突破.学生的每一次学习,都是“摸着石头过河,错误不可避免,至多只是证明某种想法或做法的可行性和不可行性.错误之后的喜悦才称得上惊喜,痛苦思索后的快乐才是痛快.
课程资源开发不仅仅是一种技巧,更应是师生心灵间自发的合作与交流.教学过程中出现的很多错误不仅给学生留下很好的思考标本,值得认真探究;更使老师能从学生的视角重新审视自己的教学设计:原先“你们怎么会这样想?”的惊讶和不可思议,便逐渐变成“哦,原来你是这样看”的理解和发现,变成“当初我在这个学习阶段也会犯这样错误”的同感和了然.
“相聚在错误树下”让学生习惯了在改正错误中前行;“相约错误”使学生思维的灵动得以展示;“相伴磨题”习得学习真功夫.他们的知识不再是只泅渡题海经验的结果,更多的是反思与提炼的结晶,在解题时也不会瞻前顾后,而是放手去做,提升自己的信心和实力.学生的课堂学习也不再是被动的浅层学习,而是真正的深度学习,成为学习的主人.我也更好的驾驭课堂,在新课改下提高了课堂教学效率,整体教学上变“瑕不掩瑜”为“金镶玉”,在教学管理上自己也由之前“拉牛上树”的纤夫变成了组织他们学习生活的领头羊,收获了更深层次的职业幸福.

