利用三角方法证明平面几何问题
浙江省绍兴市鲁迅中学 (312000) 陈少春 虞关寿
利用三角方法证明平面几何问题
浙江省绍兴市鲁迅中学 (312000) 陈少春 虞关寿
三角法证明平面几何问题就是利用正弦定理、余弦定理将平面几何中的边角关系互相转化、通过三角函数的变形公式达到证题的目的.本文通过一些数学竞赛试题,作一些探索.
1.证明平面几何中线段相等或成比例关系
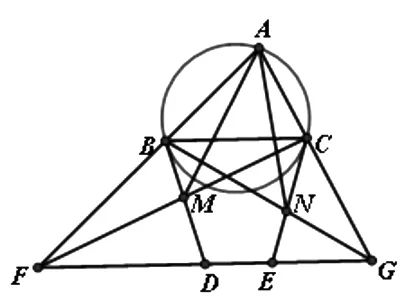
图1
例1 如图1,在锐角三角形ABC中,∠BAC≠60°,过点B,C分别作三角形ABC的外接圆的切线BD,CE,且满足BD=CE=BC.直线DE与AB,AC的延长线分别交于点F,G.设CF与BD交于点M,CE与BG交于点N.证明:AM=AN.(2014年全国高中数学联赛试题)
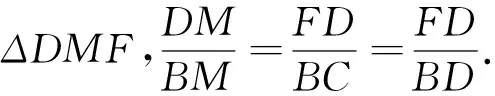
例2 如图2,PA,PB为圆O的切线,点C在劣弧AB上(不含点A,B).过点C作PC的垂线l,与∠AOC的平分线交于点D,与∠BOC的平分线交于点E.求证:CD=CE.(2013年西部数学竞赛试题)
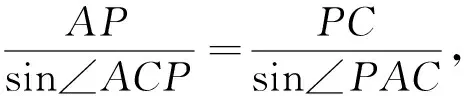
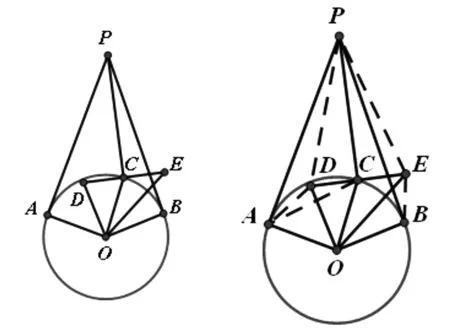
图2 图3
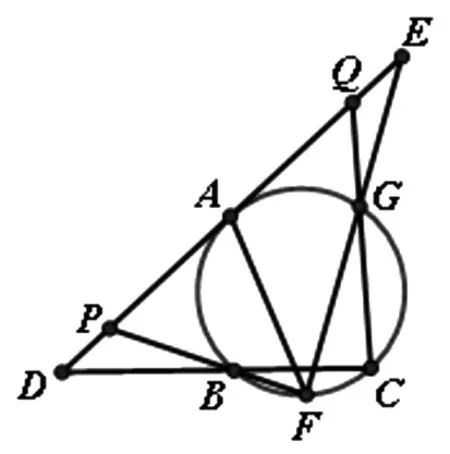
图4
例3 如图4,锐角△ABC的外接圆为圆O,过点A作圆O的切线l,l与直线BC交于点D,E是DA延长线上一点,F是劣弧BC上一点,直线EF与优弧AB交于点G,直线FB,GC分别与l交于点P、Q,证明:AD=AE的充要条件为AP=AQ.(第五届陈省身杯试题)
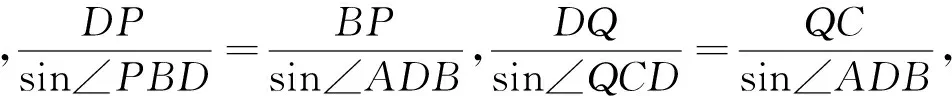
例4 如图5,AB是圆ω的一条弦,P为弧AB内一点,E、F为线段AB上两点,满足AE=EF=FB.连接PE、PF并延长与圆ω分别相交于点C、D.求证:EF·CD=AC·BD.(2013年全国高中数学竞赛试题)
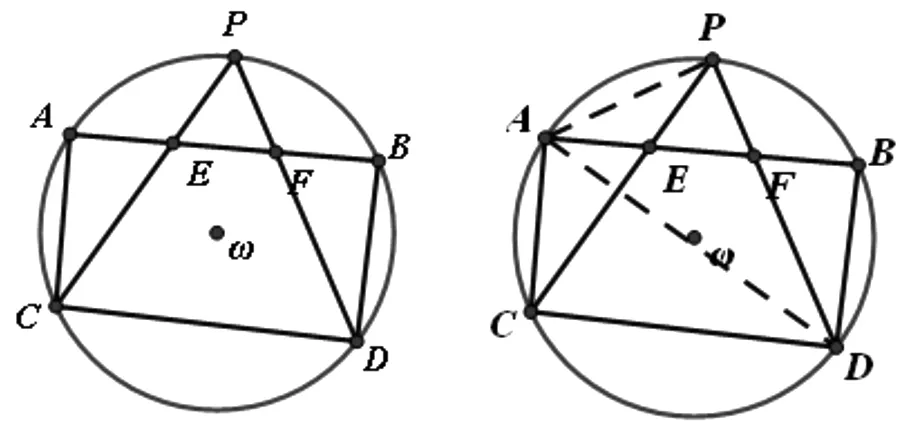
图5 图6
例5 如图7,已知ΔABC的内切圆与三边BC、CA、AB分别切于点D、E、F,AD与EF交于点G.证明:EB平分∠CEF的充分必要条件是FG=4GE.(2014年中等数学第六期)[1]
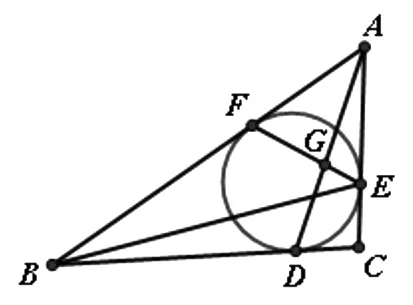
图7
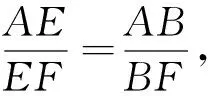
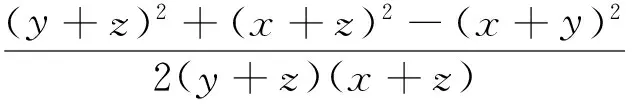
评注:①三角法解决平面几何的关键是敏锐的发现角度、边之间的关系.
②三角法的最大优点是添加的辅助线较少,当图形比较简单、角与角之间的联系比较紧密、边角关系处理比较方便时,三角法不失为一种好方法.
2.证明平面几何中的不等式
例6 在ΔABC中,已知I为内心,记ΔABC的外接圆、内切圆半径分别为R、r.证明:AI2+BI2+CI2≥6Rr.(2014年中等数学第6期)[1]
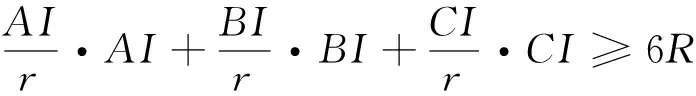
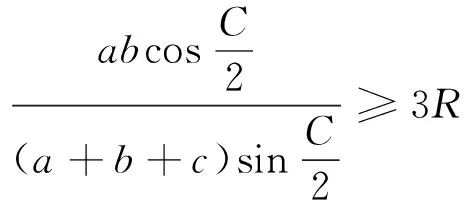
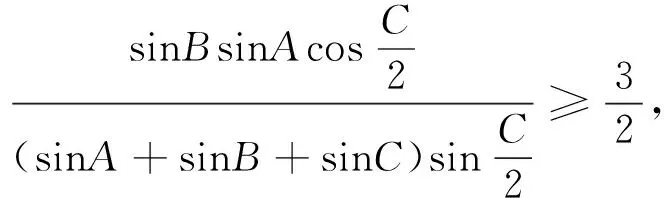
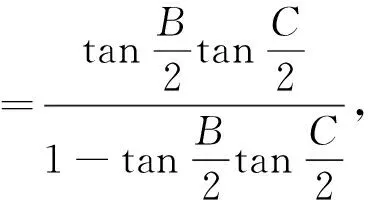
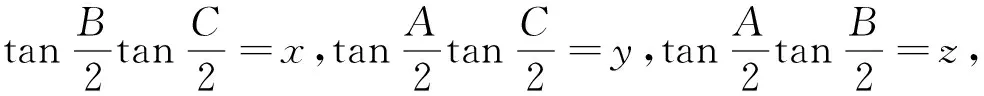
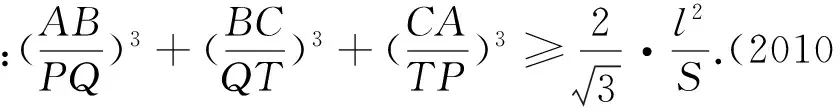
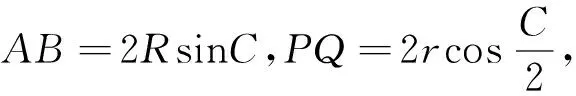
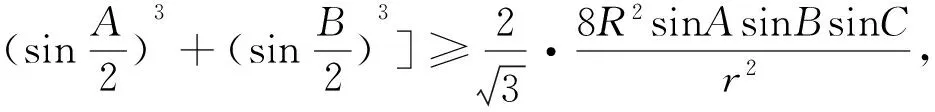
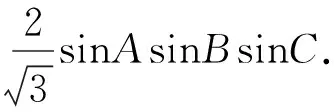
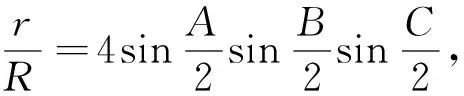
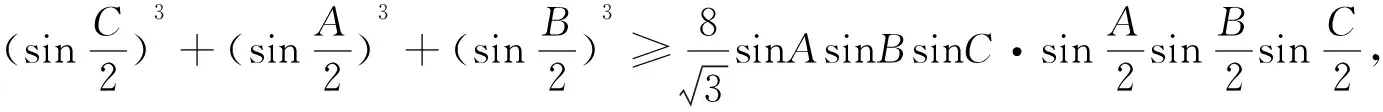
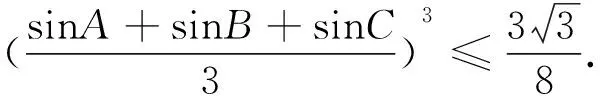
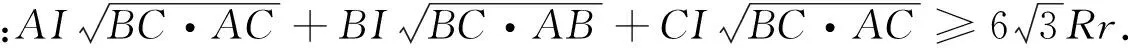
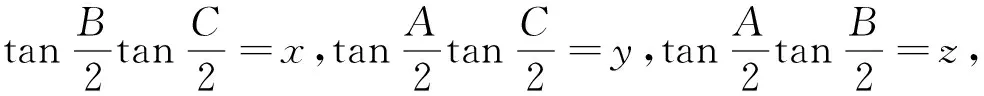
评注:利用三角法证明不等式问题需要比较扎实的三角函数基础,一些三角定理(张角定理、角平分线定理、斯德瓦特定理)和三角恒等式要会熟练运用,常用的恒等式有:
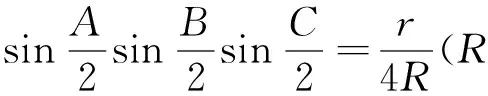
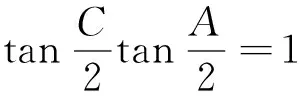
[1]数学奥林匹克问题[J].中等数学,2014(6).
[2]黄志军译.第23届韩国数学奥林匹克(2010)[J].中等数学,2011(增刊2).

