从一道高考题的教学谈数学直觉思维能力的培养

江西省南昌外国语学校 (330008) 周科春

从一道高考题的教学谈数学直觉思维能力的培养

江西省南昌外国语学校 (330008) 周科春

数学直觉思维是指对数学对象(结构及关系)进行某种直接的领悟和洞察的思维，它没有明显的根据和思索的步骤，具有跳跃性、简约性、综合性、或然性、创造性等特征．数学直觉思维能力强的人，能够快速发现数学问题的本质，切入数学问题的关键，找到解决数学问题的方法．

学生数学直觉思维能力的强弱直接影响到解题能力的指向性、多向性与敏捷性．徐治利教授曾经指出：“数学直觉是可以后天培养的，实际上每个人的数学直觉也是不断提高的”．教师在平时的教育教学过程中，特别是在解题教学过程中，应通过引导学生多方联想，整体结构上考虑问题，注意挖掘问题内部的本质联系，借助对称、和谐等数学美感，养成解题后反思的习惯等途径加以培养．以下仅通过一道立体几何高考试题的教学，谈谈如何培养学生的数学直觉思维能力．

高考真题 (2012上海理14)如图1，AD与BC是四面体ABCD中互相垂直的棱，BC=2，若AD=2c，且AB+BD=AC+CD=2a，其中a、c为常数，则四面体ABCD的体积的最大值是________．

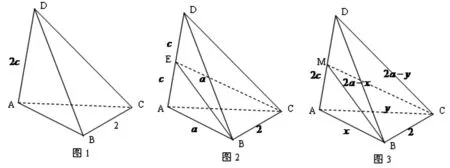
一、把握整体，敏锐观察，不以一叶障目

数学直觉思维的重要特征，是思维形式的整体性．对问题做局部的考察是必要的，但必须有整体考察的环节．放在解决数学问题时，就是要抓住问题的要点，撇去一些次要因素，放眼整体，引导学生多方位感受条件与结论，充分发挥想象力，进行大跨度、大步骤思维，着眼于从整体上揭示出问题的本质与内在联系，往往可以激发直觉思维，使得问题的解决变得简单易行．

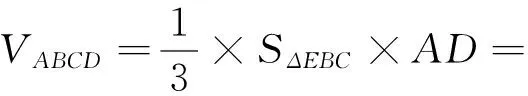
值得注意的是，直觉的发现并不能取代严格的数学证明，而只能作为后者的必要补充．因为数学是一门严谨的学科，所以许多直觉洞察的空隙必须要用逻辑推理来填补．所以在直觉发现后，要加以严格的逻辑证明，这对一个人的思维能力的发展至关重要．

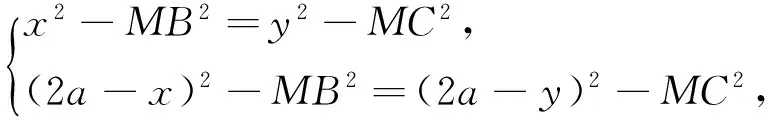
二、打破常规，巧建模型，寻求别具匠心

建立数学模型是一种重要的数学应用能力，它打破了代数与几何以及各个章节、各个知识模块之间的界线，根据题设所提供的情景，抓住问题特征，建立合适的数学模型就能够化繁为易，推陈出新，达到简化思路、出奇制胜的目的．而数学上的直觉，可以快速感知所研究的数学问题与某种数学模型的联系，感受直觉思维的别具匠心之美．

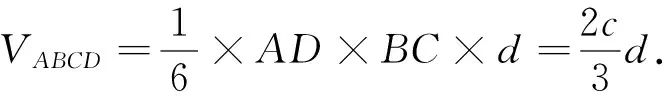
通过数学直觉思维直达有效的数学模型，还有赖于自身的数学知识的储备和思维能力的丰富和完备程度，决不可能是空穴来风．

三、探索联想，不拘一格，抓住一闪之念

联想是思维的基础，没有联想就没有创造．利用已有的知识类比联想，灵活变通，使思维处于“追求转向另一角度思考问题”的动态之中，在不断寻求的过程中通过观察、联想、类比、归纳、特殊化等方法，不放过思维的每一次闪光点，大胆的进行猜想，找到问题解决的一条又一条捷径．

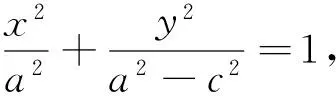
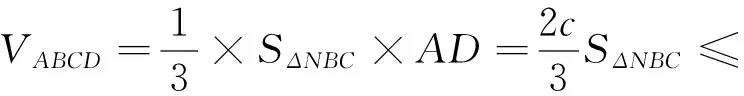
联想的角度与方向是发散的，任何条件与结论的特征都可触发联想．如由本题的空间几何体的特性，就可联想到空间直角坐标系，进而考虑利用建立空间直角坐标系的方法来求解．正所谓“联想无止境，方法无穷境”．

总之，数学直觉思维的培养是一个高品味的心智技能活动，又是一个长期渐进的过程．只有在教学活动中，时时刻刻对学生多角度、多层次的对直觉思维的过程进行展示与诱导，坚持不懈，持之以恒，一定会收获理想成效．