一维波动方程混合问题的通解

樊龙

(山西大同大学煤炭工程学院，山西大同037000)

一维波动方程混合问题的通解

樊龙

(山西大同大学煤炭工程学院，山西大同037000)

一维情形下波动方程的混合问题(初边值问题)是一类重要的物理模型，常用求解方法是波的反射原理，计算特征线在边界上的反射次数得出问题的解，但是弊端在于计算量大，且没有通用的求解公式，并不能反映出波的反射实质，另一种方法是Fourier级数法，利用分离变量将原方程化为常微分方程组，再利用常微分方程特征理论得出级数解，同样不易计算。为了简化计算过程，先对初值条件φ(x),ψ(x)根据边值条件进行相应的奇偶性延拓，可将原问题化简为初值问题，由D’Alambert公式给出问题在R上的解，再将问题的全局解限定在有限区间[0,l]上得出通解公式，结果具有一般性。

波动方程；D’Alambert公式；延拓

引言

本文主要讨论以下两类混合问题，

(1)

边值条件为

ux(0,t)=0，ux(l,t)=0，t≥0

(2)

或者边值条件为

u(0,t)=0，ux(l,t)=0，t≥0

(3)

对于以上问题求解，常用的方法有波的反射原理[1]以及Fourier级数方法(分离变量法)[2-3]。文献[4]利用特征线法，给出方程在可解区域内的通解公式，提供了另一种计算方法，文献[5]中提及了通过将函数延拓，将求解区域进行划分，然后逐个进行讨论，利用波的反射原理，给出各个可解区域内解的显示表达，最近，在文献[6]中，利用分离变量方法求解了几类特殊的波动方程，在文献[7]中利用Laplace变换对有限一维空间弹性动力学边值问题给出解的严格推导。

以往的工作都集中在具体的求解过程及方法，并未给出一个确切的解的表达式，本文的工作完善了波动方程在通解公式方面的内容，并且采用不同于以往的方法，直接利用D’Alambert公式计算，从而避开各区域讨论的繁琐过程，直接给出方程在各个区域的解的显示表达，且结果具有一般性。

1 主要结论

引理1对于问题(1)，若初始函数φ(x),ψ(x)都是关于x0的奇函数，则方程的解在任何时间都有u(x0,t)=0。

证明由达朗贝尔公式，方程的解为

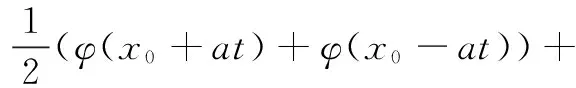
由于φ(x),ψ(x)都是关于x0的奇函数，有

φ(x0+C)=-φ(x0-C)，ψ(x0+C)=-ψ(x0-C)

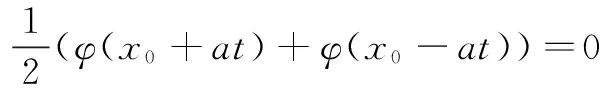
令τ=2x0-ξ

证毕。

引理2对于问题(1)，若初始函数φ(x),ψ(x)都是关于x0的偶函数，则方程的解在任何时间都有ux(x0,t)=0。

证明

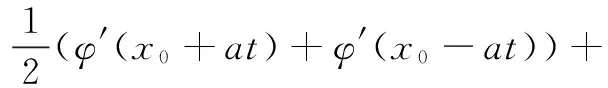
φ(x)为关于x0偶函数，则φ′(x)为关于x0的奇函数，所以ux(x0,t)=0，证毕。

由引理1和引理2，问题(1)、(2)以及(1)、(3)可对初始函数φ(x),ψ(x)进行相应的延拓，再利用达朗贝尔公式得出通解。

定理1对于问题(1)、(2)，对函数φ(x),ψ(x)对于点x=0,x=l均作偶延拓，即

(-1)m-1(m+δm)l]+φ[(-1)n(x-at)+

(-1)n-1(n+δn)l]}+

定理2对于问题(1)、(3)，对函数φ(x),ψ(x)关于x=0作奇延拓，对函数φ(x),ψ(x)关于x=l作偶延拓即

u(x,t)=

其中δk定义同定理1。

2 结论证明

定理1的证明：首先问题(1)、(2)的解可用达朗贝尔公式表示

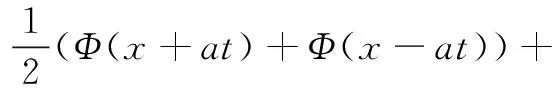
(4)

由引理1、引理2以及Φ(x)，Ψ(x)均为关于x=1,x=l的偶函数，可知ux(0,t)=0，ux(l,t)=0，满足边值条件。

由Φ(x),Ψ(x)的定义，容易得到

(5)

(6)

分析积分部分，将问题分情况讨论：

(1)n为偶数，m为偶数

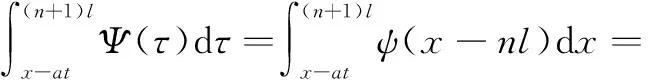
由于Ψ(x)是关于x=0,l的偶函数，所以对于k∈Ζ有

进而

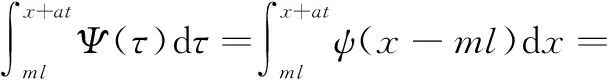
综合

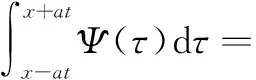
(2)n为奇数，m为偶数

同理，

(3)n为偶数，m为奇数

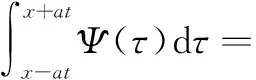
(4)n为奇数，m为奇数

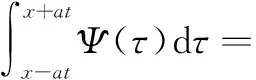
所以

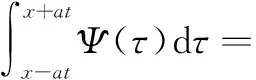
(7)

将式(5)、式(7)代入式(4)，定理1证毕。

定理2的证明：方法类似于定理1，由引理1、引理2以及Φ(x)，Ψ(x)的定义，可知u(0,t)=0,ux(l,t)=0；易知

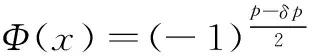
(8)

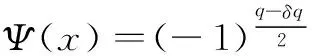
(9)

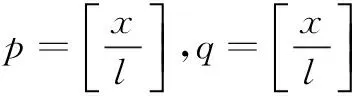
(1)n为偶数，m为偶数

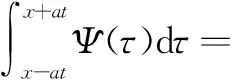
由(9)式可知

因为Ψ(x)是关于2kl(k∈Z)的奇函数，且m,n均为偶数，所以

同理

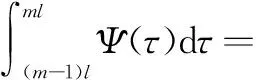
所以可得

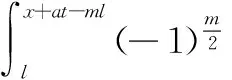
(2)n为奇数，m为偶数

同理，

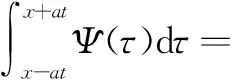
(3)n为偶数，m为奇数

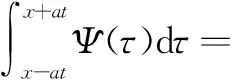
(4)n为奇数，m为奇数

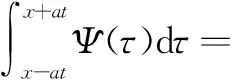
综合可得

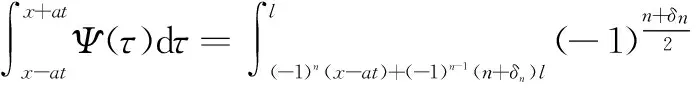
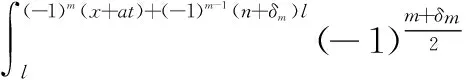
(10)

将式(8)、式(10)代入式(4)，定理2证毕。

推论1当边值条件为u(0,t)=0，u(l,t)=0，t≥0，解为

u(x,t)=

(-1)nφ[(-1)n(x-at)+(-1)n-1(n+δn)l]}+

推论2当边值条件为ux(0,t)=0，u(l,t)=0，t≥0，解为

u(x,t)=

证明过程类似定理1，定理2，在此省略。

3 实例

求解如下混合问题

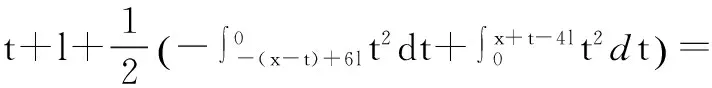
其他区域同理，这也体现了在不同区域，由于沿各边界反射次数不同，所以得到不同形式的解，反映出波的反射原理的实质。

[1]朱长江,邓引斌.偏微分方程教程.北京:科学出版社,2005.

[2]谷超豪,李大潜,陈恕行,等.数学物理方程.2版.北京:高等教育出版社,1996.

[3]陈恕行,秦铁虎,周忆.数学物理方程.上海:复旦大学出版社,2003.

[4]姜玲玉.关于波动方程混合问题的特征线方法.数学杂志,2004,24(5):577-580.

[5]赵天玉,毛占军.求解波动方程混合问题的通解函数延拓法.长江大学学报:自然科学版,2005,2(1):4-9.

[6]王心平.分离变量法在求解波动方程中的应用.科技视界,2014,35:60-61.

[7]赵福垚,宋二祥.有限一维弹性波动问题的公理化求解及其在自由场中的应用.工程力学,2015(4):47-53.

[8]杜心华.一类非线性波动方程混合问题整体解的存在唯一性.四川师范大学学报:自然科学版,1994(4):10-14.

[9]杨萌.可控一维波动方程的边值混合问题.湖北理工学院学报,2008(6):55-58.

[10]梁志辉,李之杰.一维波动方程混合问题的差分解.内蒙古民族大学学报,2009(2):5-6.

[11]赵天玉.求解波动方程混合问题的曲线积分法.长沙大学学报,2005(2):1-3.

[12]林琼桂.高维波动方程与热传导方程非齐次边界条件的一般处理.大学物理,2015(5):1-4.

[13]WALTER A S.Partial Differential Equations-An Introduction.New York:John Wiley&Sons Inc,1992.

[14]RAUCH J.Partial Differential Equations.New York:Springer-Verlag,1991.

[15]洪洁.一类非线性波动方程混合问题解的爆破.兰州理工大学学报,2004(3):124-126.

The General Solution to Mixed Problem of a 1D Wave Equation

FANLong

(School of Coal Engineering, Shanxi Datong University, Datong 037000, China)

The mixed problem of 1D wave equation is an important model in physics. The most commonly used method is the principle of reflection wave, which calculates the number of reflection on the boundary to obtain the solution of the problem, but the disadvantage of this method is that the scale of calculation is large and general formula is not given, at the same time, the essence of reflection is not reflected. Another method is the Fourier series which is also hard to calculate. With method of Fourier series, ordinary differential equations can be obtained by separation of variables, then the problem is solved by using characteristic method. In the purpose of simplifying the calculation, taking corresponding extension of initial valueφ(x),ψ(x)accordingtotheboundaryvalue,theproblemcanbesimplifiedintotheformofinitialproblem,thenthesolutioninRcanbegotbyusingD’Alambert’sformula,andthegeneralsolutionistherestrictionofglobalsolutionon[0,l],meanwhiletheresultisgeneral.

wave equation; D’Alambert’s formula; extensions

2016-11-27

山西大同大学教学改革项目(XJY2013211)

樊 龙(1989-)，男，山西忻州人，助教，硕士，主要从事偏微分方程方面的研究，(E-mail)fanlongmath@163.com

1673-1549(2017)01-0092-05

10.11863/j.suse.2017.01.18

O175.27

A