具有二维间隙非线性的全动舵面动力特性研究

陈识， 李秋彦， 冉玉国

(成都飞机设计研究所， 成都610091)

具有二维间隙非线性的全动舵面动力特性研究

陈识， 李秋彦， 冉玉国

(成都飞机设计研究所， 成都610091)

由于存在不同方向的间隙非线性因素，在飞机全动舵面GVT试验中发现：激励点不同，测试得到的模态结果有较大差异。通过分析全动舵面操纵系统各个环节对间隙的影响，在特定的激励点采用渐进加力法进行GVT试验，研究了旋转和弯曲二维间隙对旋转和扭转模态的影响。运用MSC.NASTRAN软件建立FEM模型进行了模态分析，研究间隙对其动力特性的影响，并与试验结果进行对比。研究结果表明，GVT试验与FEM模型分析结果有较好的相关性，并给出了不同方向的间隙非线性对全动舵面固有振动特性的影响。

二维间隙非线性；全动舵面；固有振动特性； GVT试验；变参数分析

引言

由于生产中的超差、装配误差以及运动过程中的磨损等因素，间隙非线性[1-3]是飞行器中最常见的一种结构非线性。全动舵面操纵系统同样不可避免地存在着间隙，这会导致支持系统刚度下降，从而影响其动力特性。然而，现代歼击机的设计广泛采用了直轴与电传伺服操纵系统的全动舵面，通常该结构布局的颤振安全余量处于临界状态，颤振速度随弯曲模态、扭转模态变化十分敏感。因此，在分析计算和地面共振试验(GVT)中，获得全动舵面准确、合理的固有振动特性一直是型号设计与试验单位重点关注的难题。

为了预防和消除不希望发生的气动弹性不稳定现象，同时也为先进飞行器设计提供理论依据，含间隙结构的非线性动力学问题成为近年来国内外学者以及工程人员的研究热点[4-7]。但是大多数研究都局限于一维旋转间隙，并且自由度较少的简单结构系统，很难有效地解决实际工程中复杂结构问题。目前在试验方面，国内处理具有间隙非线性特征全动舵面主要是采用渐进加力法来克服间隙非线性的影响。在试验过程中，通过增加激振力的方式可绘制出“力-频”(激振力-频率)曲线，把大激振力下模态指示函数较高并且稳定的频率、振型作为它的固有振动特性。在分析计算方面，工程问题通常采用等效刚度概念，建立有限元模型(FEM)进行分析。例如，William D等人利用经典的颤振分析方法以及等效刚度分析F-22飞机的动力特性，并进行颤振和嗡鸣评估[8]。

在某型飞机全机GVT试验中，由于旋转间隙不满足国军标规范要求(全动舵面的自由间隙应该小于0.034°)，决定采用渐进加力法对该型飞机的全动舵面进行模态测试。在试验过程中发现，在不同的激振点进行激励，得到的“力-频”曲线有较大差异，这会导致FEM模型修正误差，从而进一步影响颤振分析的正确性。为了查明本次试验结果分散性较大的原因，通过对试验数据及现场飞机状态的分析，排除飞机各部件间的模态干扰以及试验中模态识别误差等因素，发现该全动舵面除了旋转间隙外，还存在绕翼面根弦方向的弯曲间隙。为弄清旋转、弯曲二维间隙对该全动舵面动力特性的影响，分别在旋转、弯曲方向相应的激振点对该舵面进行激励，得到对应的GVT结果。文中采用MSC.NASTRAN软件建立FEM模型，利用等效刚度概念对该结构的二维间隙进行模拟。通过SOL103求解器可计算出该结构的振动特性，并设置刚度控制因子进行变参数分析，得到旋转、一扭模态随刚度变化的情况。通过试验与分析计算结果对比分析可知，旋转和弯曲二维间隙非线性因素[9]是导致差异的重要原因。

1 含间隙系统的数学描述

1.1 含间隙的单自由度系统描述

含间隙的舵面可以看作是一个带间隙的单自由度系统，该系统可用图1 进行描述。

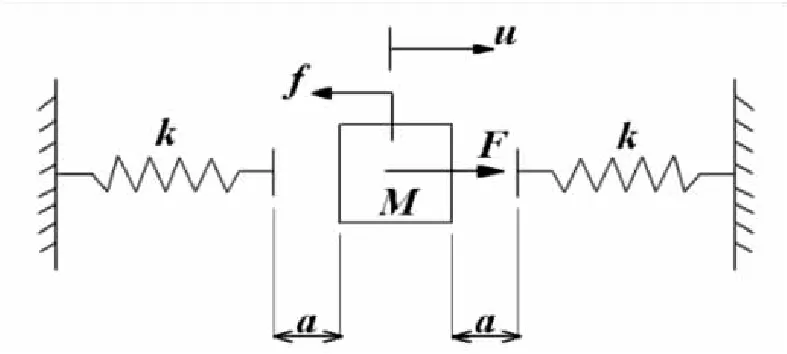
图1 带间隙的单自由度系统

图1 中，u为质量块位移，以间隙中心点为位移u=0；a为中心型间隙的一侧间隙；M为质量块质量；k为弹簧刚度；f为质量块运动过程中所受的摩擦力；F为质量块系统所受的外激振力。通过对质量块进行受力分析得到系统的力学分段表达式：

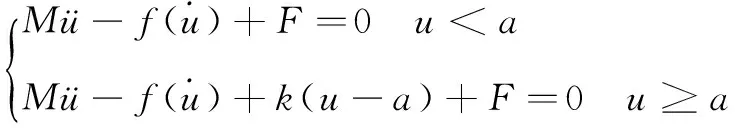
(1)

式中：当质量块位移时，质量块未克服间隙，其响应为强迫振动，振动频率为激振力频率；当质量块位移时，该系统的解分为两部分，第一部分为结构系统的自由衰减运动，随着时间的增加趋近于0，第二部分为强迫振动。

分段(间隙段与非间隙段)分析含间隙系统的力学特性时，不存在系统的线性等效过程，很难得到两段过程统一的数学表达。而在实际工程GVT试验中，测试的是含间隙结构的模态特性，即此时已默认将系统作为线性系统来进行分析(等效线性化处理)。一个激励幅值下只产生一个结构频率，此时测得的结构频率即为此时系统等效刚度的反映特性。因此，为了研究激振幅值(或激振力大小)对测得的结构频率(结构等效刚度)影响，工程中普遍认同等效刚度的概念。

1.2 含间隙系统的等效刚度

根据等效线性化理论，常见的间隙包括中心型间隙和带预载偏移型间隙[10]。用图2 (a)可表示旋转系统的间隙情况，其中为外部力矩，为转角，为无间隙状态旋转刚度，为旋转间隙。实际工程结构中，中心间隙型非线性刚度是不存在的，一般都是带预载偏移型非线性刚度，如图2 (b)所示，相当于间隙位置被“平移”到了～。

图2 间隙非线性刚度示意图

含间隙全动舵面的GVT试验[11]，无论是中心间隙还是带偏置情况间隙，对于间隙不大的情况，用逐渐增加激振力的方式可绘制出“力-频”曲线，从而获得含间隙结构的频率，如图3 所示。

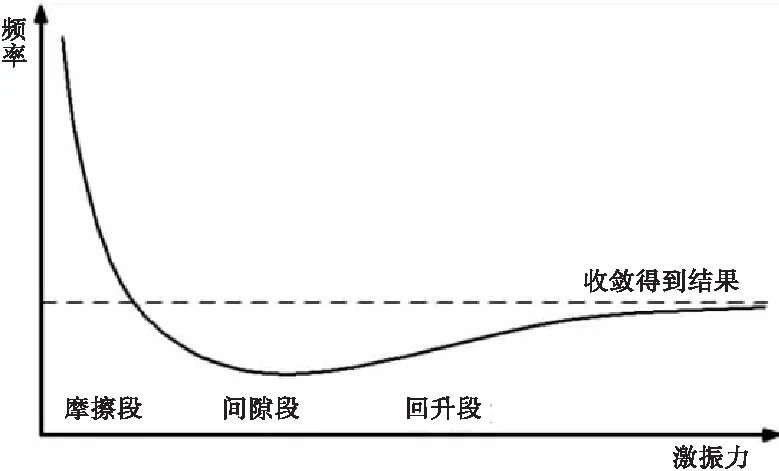
图3 GVT试验“力-频”曲线

从图3 可看出，在不断增大激振力的过程中含间隙结构的频率(等效刚度)经过克服摩擦、克服间隙段、频率回升、最终收敛得到接近真实刚度的结果。

2 全动舵面GVT试验及数据分析

本文描述的全动舵面模态测试在某型飞机全机状态下进行，采用渐进加力法克服间隙非线性的影响。这次试验使用模态参数的频响函数识别法，通过激振器对飞机施加一定的激振力，用LMS模态试验系统采集处理各响应测量点的加速度响应和各激励点的力信号，并按模态参数识别理论的有关方法识别试验所要求的各模态参数。

该全动舵面通过转轴安装在机身内外侧支撑结构上，如图4 所示，整个操纵系统由转轴、摇臂、ISA助力器、ISA支座以及内/外端轴承组成。根据目前国内生产工艺条件，以及其他自研型号全动舵面经验来看，旋转间隙主要来自于ISA助力器本身，摇臂/转轴、ISA/摇臂、ISA助力器及其支座间的配合；弯曲间隙主要来自于轴承本身间隙以及转轴/内外端轴承、机身支撑结构/内外端轴承间的配合。

图4 全动舵面操纵结构示意图

在试验过程中，整个翼面共布置24个测量点，每个测量点包括法向和面内传感器，如图5 所示。为了克服旋转(绕Y方向转动)、弯曲(绕X方向转动)间隙，分别在1#点、19#点进行变力激励，测量旋转模态和一扭模态。试验测试得到的频率结果(归一化处理)见表1 、表2 ，模态振型如图6 所示。

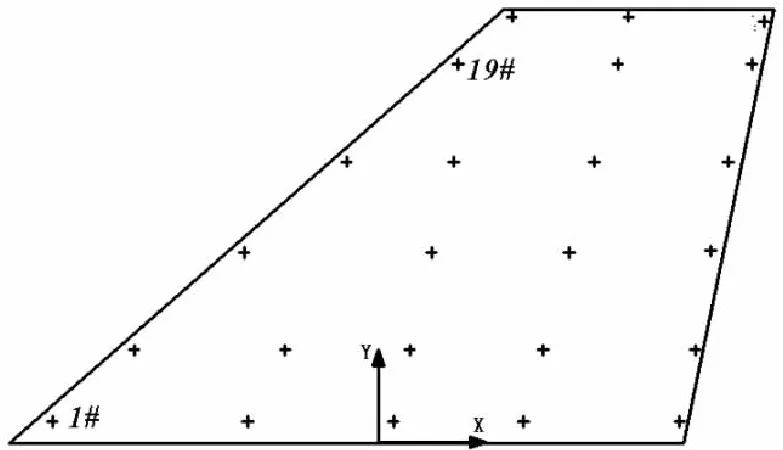
图5 测量点布置图

表1 旋转频率变力试验结果

表2 一扭频率变力试验结果

图6 模态振型(GVT试验)

根据表1 ～表2 的变力试验结果可绘制旋转模态、一扭模态“力-频”曲线，如图7 ～图8 所示。

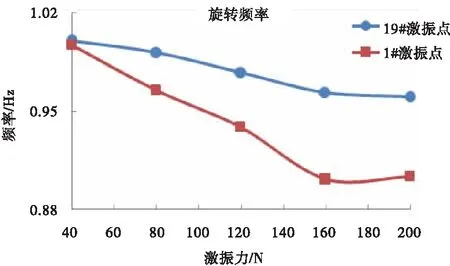
图7 旋转模态“力-频”曲线

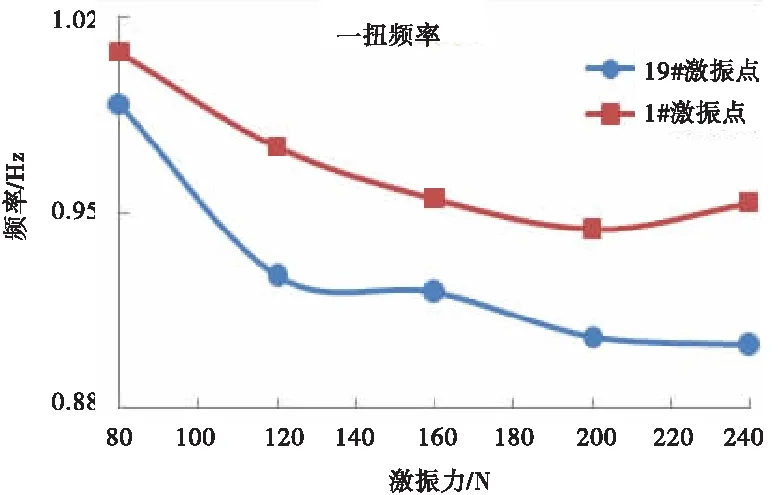
图8 一扭模态“力-频”曲线

根据表1 的试验结果以及图7 曲线变化趋势可知：针对该全动舵面，无论在1#点还是19#点进行激励，在激振力为40N时得到的旋转频率基本一致，说明此时结构还没有开始克服结构的摩擦。随着激振力的增加，旋转频率逐渐减小，最终“力-频”曲线趋于平缓并且有收敛趋势，这说明结构进入间隙段并克服了间隙，也反映了旋转频率同时受旋转、弯曲二维间隙的影响。对比图7 中两条曲线可发现：当激振力施加到200N时，在1#激振点进行激励得到的旋转频率收敛值明显小于19#激振点的收敛值，表明旋转方向的间隙是旋转频率的主要影响因素。同理，根据表2 和图8 可得到相似结论：随着激振力的增加一扭频率大幅下降，这说明旋转、弯曲二维间隙对一扭频率都有很大影响。从图8 中两条一扭模态的“力-频”曲线收敛值看出弯曲方向间隙对一扭频率影响更大。

3 全动舵面仿真分析

根据全动舵面真实结构建立动力FEM模型，为了体现旋转、弯曲二维间隙的影响，根据等效刚度概念，采用绕转轴方向以及绕根弦方向的两根旋转弹簧模拟机身结构及操纵系统的旋转刚度和弯曲刚度。通过刚度控制因子保持旋转、弯曲刚度其中一个为设计值的情况下，对另外一个刚度进行变参数分析。旋转频率、一扭频率计算结果(归一化处理)见表3 、表4 ，相应的模态振型如图9 所示。

表3 旋转频率变刚度计算结果

表4 一扭频率变刚度计算结果

图9 模态振型(FEM计算)

将表3 ～表4 的数据绘制成旋转频率、一扭频率随刚度控制因子变化曲线，如图10 ～图11 所示。

图10 旋转频率随刚度变化曲线

图11 一扭频率随刚度变化曲线

通过对比全动舵面仿真分析结果与第2节所述的GVT试验结果可知：旋转、一扭模态频率随刚度控制因子变化曲线与“力—频”曲线变化趋势一致，并且模态振型吻合得很好，说明全动舵面的FEM模型真实地模拟了该结构动力特性。

根据计算分析结果可知：针对旋转、一扭振型节线如图9 所示的全动舵面，在弯曲刚度变化不大的情况下旋转频率变化较小，说明旋转频率对弯曲刚度不敏感。但是随着旋转刚度下降，旋转频率大幅度降低，说明旋转刚度对旋转频率有着决定性影响。然而无论旋转刚度还是弯曲刚度下降都会导致一扭频率下降，这反映出一扭频率同时受到旋转刚度和弯曲刚度的影响。随着刚度因子的下降，旋转刚度下降引起的一扭频率降低幅度小于弯曲刚度引起的一扭频率降低幅度，说明弯曲刚度对一扭频率的影响大于旋转刚度对该频率的影响。

4 结论

通过本次全动舵面GVT试验以及计算分析，可以得出以下结论：

(1) 旋转和弯曲二维间隙非线性是导致GVT试验结果有差异的主要原因。由于二维间隙的存在，全动舵面的旋转和弯曲刚度都受到损失造成频率降低。旋转频率主要受到旋转间隙的影响，但是一扭频率同时受到旋转和弯曲二维间隙的影响。

(2) GVT试验获得的旋转、弯曲二维间隙对该全动舵面旋转、一扭模态特性的影响与变刚度计算分析得到的规律有较好的一致性。采用等效刚度概念通过弹簧元模拟旋转、弯曲刚度，将两个方向的刚度解耦，能很好的对二维间隙导致的刚度变化进行模拟，在工程上有较强的实用性。

[1]史爱明,杨永年,叶正寅.带结构刚度非线性的超音速弹翼颤振分析方法研究.西北工业大学学报,2003,21(4):481-486.

[2]李道春,向锦武.控制面间隙对非线性二元机翼气动弹性响应的影响.航空学报,2009,30(8):1385-1391.

[3]CHEN P C,LEE D H.Flight-loads effect on free-play induced limit cycle oscillation//Proceeding of 47th AIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics,and Materials Conference,Newport,RhodeIsland,May 1-4,2006:1851-1857.

[4]张鹏,冉景洪.舵面系统间隙非线性气动弹性研究.航空兵器,2010(5):3-6.

[5]赵永辉,胡海岩.具有操纵面间隙非线性二维翼段的气动弹性分析.航空学报,2003,24(6):521-527.

[6]李毅,杨智春,金伟.操纵面非线性气动弹性响应引起的结构疲劳损伤分析方法研究.振动与冲击,2015,34(11):41-45.

[7]TANG D,DOWELL E H,VIRGIN L N.Limit cycle behavior of an airfoil with a control surface.Journal of Fluids and Structures,1998,12(7):839-858.

[8]ANDERSON W D,MORTARA S.Maximum control surface free play,design and flight testing approach on the F-22//Proceeding of 48th AIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics,and Materials Conference,Honolulu,Hawaii,April 23-26,2007:1767-1773.

[9]陈明凤,刘炜,金玉华.折叠舵间隙非线性颤振分析研究.现代防御技术,2013,41(1):15-19.

[10]刘超峰,张赢,杨智春.间隙结构的非线性气动弹性方法和行为研究.上海航天,2015,32(4):33-40.

[11]ANDERSON W D,MORTARA S.F-22 aeroelastic design and test validation//Proceeding of 48th AIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics,and Materials Conference,Honolulu,Hawaii,April 23-26,2007:1760-1766.

Research on the Vibration Characteristics of an All-movableWing with Two Dimensional Freeplay Nonlinearity

CHENShi,LIQiuyan,RANYuguo

(Chengdu Aircraft Design and Research Institute, Chengdu 610041, China)

In aircraft Ground Vibration Test (GVT), there are variations among the modal test results measured at different excitation positions, which are supposed to be caused by freeplay nonlinearity in different directions. The control system of all-movable wing is composed of several different components, whose contributions to the freeplay nonlinearity are researched. Then the effect of a 2-dimensional freeplay, rotational as well as bending, to rotation and torsion modes are studied by GVT test using the step-forcing method at variation of given excitation positions. A Finite Element Model (FEM) is built in MSC.NASTRAN, by which the affection of freeplay to vibration characteristics is studied numerically in mode analysis. Finally, the numerical results are compared to test results. The researches show good correlation between GVT result and analysis result in FEM, and the effect of freeplay in different directions for natural vibration characteristics has been concluded detailedly.

two-dimensional freeplay nonlinearity; all-moving rudder; vibration characteristics; ground vibration test; parameters analysis

2016-04-06

陈 识(1985-),男,贵州都匀人,工程师,硕士,主要从事气动弹性、模态参数识别方面的研究,(E-mail)liaoshi2317@163.com; 李秋彦(1964-),男,四川达州人,研究员,博士,主要从事气动弹性、气动伺服弹性方面研究,(E-mail)li-qiuyan@163.com

1673-1549(2017)01-0060-05

10.11863/j.suse.2017.01.11

V211.43

A