双重Stone代数的核理想
赵秀兰, 陈丽娟
(1.黄河科技学院数理部, 郑州450063;2.河南工程学院理学院, 郑州451191)
双重Stone代数的核理想
赵秀兰1, 陈丽娟2
(1.黄河科技学院数理部, 郑州450063;2.河南工程学院理学院, 郑州451191)
理想是研究Ockham代数类结构的一个重要工具,在双重Stone代数上引入核理想的概念,构造了核理想同余关系表达式,获得了双重Stone代数核理想判别定理。根据双重Stone代数的运算特征及主同余表示理论,获得了核理想同余关系的若干等价表达式并证明了双重Stone代数核理想与其同余关系是同构的。所得结论为其它Ockham代数类核理想性质的研究提供了方法,丰富了Ockham代数的发展,为进一步研究Ockham代数类的代数结构提供理论支持。
Stone代数;对偶Stone代数;双重Stone代数;核理想;同余关系
Ockham代数[1]是定义在分配格上的一类序代数,布尔代数、de Morgan代数、Stone代数、伪补代数等是Ockham代数的子代数。作为Stone代数、de Morgan代数的共同概括,Blyth引入MS代数[2]的概念,给出了MS代数的运算性质,获得了MS代数主同余表示定理。在序代数结构的研究中,常根据理想和滤子的性质来反映序代数结构。文献[3-13]以理想与滤子为工具刻画代数结构。文献[5]证明了PO代数类上具有余核滤子的最小同余和最大同余。文献[9]研究了平衡半拟补Ockham代数的余核滤子和稠密滤子的特征,并刻画这些滤子的某些同余一致与同余凝聚性质。文献[10]分别就双重伪补代数的假值理想、假值同余和几乎伪补格的核理想与W-理想[11]给出了特征表示。本文将在此基础上构造双重Stone代数核理想同余关系表达式,论证核理想与其同余关系之间的关联性。
1 预备知识
定义1[1]设(L;∧,∨,0,1)是一个有界分配格,f是L上的一元运算,若:
(1)∀x,y∈L,f(x∧y)=f(x)∨f(y),f(x∨y)=f(x)∧f(y)
(2)f(0)=f(1),f(1)=f(0)则称(L;∧,∨,f,0,1)是一个Ockham代数(简记为O)。
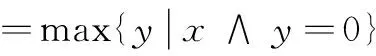
一个伪补代数(L;∧,∨,*,0,1),如果运算*满足条件:∀x∈L,x*∨x**=1,称(L;∧,∨,*,0,1)为Stone代数。

定义3[1]设(L;∧,∨,0,1)是一个有界分配格,其上赋予两个一元运算*,+,并且(L;∨,∧,*)是Stone代数,(L;∨,∧,+)是对偶Stone代数,称(L;∨,∧,*,+)是一个双重Stone代数。
引理1[1,14-15]设(L;∨,∧,*,+)是一个双重Stone代数,任意的x,y∈L,则
(1)x*≤x+;
(2)x+*=x++≤x≤x**=x*+;
(3)0*=1,1*=0,x*=x***,0+=1,1+=0,x+=x+++;
(4)(x∧y)*=x*∨y*,(x∨y)*=x*∧y*;
(5)(x∧y)+=x+∨y+,(x∨y)+=x+∧y+;
(6)x*∨x**=1,x+∨x++=1。
定义4设(L;∨,∧,*,+)是一个双重Stone代数,θ是L的格同余关系,若(x,y)∈θ(x*,y*)∈θ,(x+,y+)∈θ,则称θ是L的同余关系,符号ConL表示L的全体同余关系构成的集合。
引理2[1]设(L;∨,∧,o,+)是一个双重MS代数,a,b∈L,a≤b,则
θ(a,b)=θlat(a,b)∨θlat(bO,aO)∨θlat(aOO,bOO)∨θlat(b+,a+)∨θlat(a++,b++)
双重Stone代数是双重MS代数的子代数,故双重Stone代数(L;∨,∧,*,+,0,1)的主同余关系式为:
θ(a,b)=θlat(a,b)∨θlat(b*,a*)∨θlat(a**,b**)∨θlat(b+,a+)∨θlat(a++,b++)
定义5设(L;∧,∨)是一个格,I是格L的子格,若x,y∈L,y≤x∈I总有y∈I,称子格I是格L的理想。
对偶地,F是格L的子格,若x,y∈L,y≥x∈F总有y∈F,称子格F是格L的滤子。

便于阐述,假定L是双重Stone代数,a,b∈L,F⊆L,符号θ(a,b)和θlat(a,b)分别表示包含a,b的最小同余与最小格同余(即由a,b所生成的主同余和格主同余),用θ(F)和θlat(F)分别表示包含F的最小同余与最小格同余(即由F所生成的主同余和格主同余)。
2 核理想的性质
给出双重Stone代数核理想判别定理。
定理1设(L;∨,∧,*,+,0,1)是一个双重Stone代数,I是L的理想,则I是核理想的充要条件是(a∈L)a∈Ia**∈I。
证明充分性 若I是L的核理想,则存在φ∈ConL,使得I=Kerφ。设a∈I,故a≡0(φ),从而a**≡0(φ),所以a**∈I。
必要性 设a∈L,a∈I蕴涵a**∈I。在L上定义一个等价关系δI:(x,y)∈δI(∃i∈I)x∨i=y∨i。易得,δI是一个格同余。
现证δI∈ConL。设(x,y)∈δI,则存在i∈I,使得x∨i=y∨i。从而有
x*∧i*=y*∧i*,x+∧i+=y+∧i+
i**∨(x*∧i*)=i**∨(y*∧i*),i++∨(x+∧i+)=
i++∨(y+∧i+)
由引理1知,i*∨i**=1,i+∨i++=1,根据双重Stone代数运算的分配性可得i**∨x*=i**∨y*,i++∨x+=i++∨y+。在双重Stone代数中,由引理1知,任意的x∈L,x++≤x≤x**,所以可得i**∨x+=i**∨y+。由题设知,i**∈I。所以(x*,y*)∈δI,(x+,y+)∈δI,因此δI∈ConL。
下证I=KerδI。设x∈KerδI,即(x,0)∈δI,则存在i∈I,使得x∨i=i,从而x≤i∈I,故x∈I,因此KerδI⊆I。另一方面,设i∈I,由题设知i**∈I。由引理1知,i≤i**,故i∈KerδI,从而有I⊆KerδI。所以I=KerδI。
设(L;∨,∧,*,+,0,1)是一个双重Stone代数,由定理1知,δI∈ConL且I=KerδI,进一步可得δI的其它性质。记I(L)和KI(L)分别为L的所有理想与所有核理想构成的集合。I(L),KI(L)具有下列性质。
推论1设(L;∨,∧,*,+,0,1)是一个双重Stone代数,I,J∈KI(L),则
(1)(∀φ∈ConL)I=KerφδI≤φ;
(2)I≤JδI≤δJ。
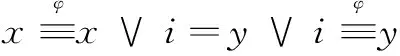
(2)设I,J∈KI(L),且I≤J。由δI,δJ的定义知,δI≤δJ。另一方面,若δI≤δJ,则KerδI≤KerδJ,又由定理1的证明知,I=KerδI,J=KerδJ,所以I≤J。
定理2KI(L)是I(L)的一个子格。
证明令I,J∈KI(L),下证I∧J,I∨J∈KI(L)。
设x∈I∧J,则x∈I,x∈J。又因I,J∈KI(L),由定理1知,x**∈I且x**∈J。故x**∈I∧J,又由定理1知,I∧J∈KI(L)。令x∈I∨J,由文献[16]知,存在i∈I及j∈J,使得x≤i∨j,从而x**≤i**∨j**。又因I,J∈KI(L),所以由定理1知,i**∈I且j**∈J。因此x**∈I∨J。从而由定理1得I∨J∈Ik(L)。所以Ik(L)是I(L)的一个子格。
3 核理想的同余关系
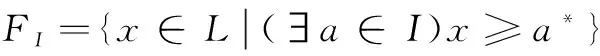
定理3设(L;∨,∧,*,+,0,1)是一个双重Stone代数,I是L的核理想,则θ(I)=θlat(I)∨θlat(FI)。
证明设a,b∈L且a≤b,由引理2知,
θ(a,b)=θlat(a,b)∨θlat(b*,a*)∨θlat(a**,b**)∨θlat(b+,a+)∨θlat(a++,b++)
由定理1知,a**,b**∈I,又因a++≤a,a+≥a*,b++≤b,b+≥b*,故a++,b++∈I,a*,b*,a+,b+∈FI,故
θlat(a,b),θlat(a**,b**),θlat(a++,b++)≤
θlat(I),θlat(b*,a*),θlat(b+,a+)≤θlat(FI)

另一方面,易见θlat(I)≤θ(I)。设a,b∈FI且a≤b,由FI的定义知,存在c∈I,使得b≥a≥c*。又因(0,c)∈θ(I),因此(c*,1)∈θ(I),故(a∨c*,a∨1)∈θ(I),(b∨c*,b∨1)∈θ(I),从而有,(a,1)∈θ(I),(b,1)∈θ(I),故得(a,b)∈θ(I)。
进一步地,用另一种形式刻画θ(I)。
定理4设(L;∨,∧,*,+,0,1)是一个双重Stone代数,I是L的核理想,则
(x,y)∈θ(I)(∃a,b∈I)(x∨a)∧b*=
(y∨a)∧b*
证明定义L上一个等价关系φ:
(x,y)∈φ(∃a,b∈I)(x∨a)∧b*=
(y∨a)∧b*
易见,φ是一个格同余关系。
下证φ∈ConL。设(x,y)∈φ,则存在a,b∈I,使得(x∨a)∧b*=(y∨a)∧b*。故
(x*∧a*)∨b**=(y*∧a*)∨b**
(x+∧a+)∨b*+=(y+∧a+)∨b*+
根据运算的分配性有,
(x*∨b**)∧(a*∨b**)=(y*∨b**)∧
(a*∨b**)
(x+∨b*+)∧(a+∨b*+)=(y+∨b*+)∧(a+∨b*+)
根据Stone代数的运算性质有,a*=a***,a*∨b**=(a∧b*)*,且a∧b*≤a∈I,则a∧b*∈I。又因a+≥a*,故(a+∨b*+)∧a*=a*,因此(x+∨b*+)∧(a**)*=(y+∨b*+)∧(a**)*。又因I是L的核理想,由定理1知,a**,b**=b*+∈I,所以(x*,y*),(x+,y+)∈φ。因此φ∈ConL。
现证φ=θ(I)。设(x,y)∈φ,则存在a,b∈I,使得(x∨a)∧b*=(y∨a)∧b*。因为(a,0)∈θlat(I),(b*,1)∈θlat(FI),所以(x,x∨a)∈θlat(I),((x∨a)∧b*,x∨a)∈θlat(FI),因此(x,(x∨a)∧b*)∈θlat(I)∨θlat(FI)。
同理可得,(y,(y∨a)∧b*)∈θlat(I)∨θlat(FI)。所以(x,y)∈θlat(I)∨θlat(FI),即φ≤θlat(I)∨θlat(FI),由定理3知,φ≤θ(I)。
另一方面,设(x,y)∈θ(I)=θlat(I)∨θlat(FI),则存在x=x0,x1,...,xn-1=y且(xi,xi+1)∈θlat(I)或者(xi,xi+1)∈θlat(FI)(i=0,1,2,...,n-2)。
因此(x,y)∈φ,故θ(I)≤φ。定理得证。
推论2设(L;∨,∧,*,+,0,1)是一个双重Stone代数,I是L的核理想,x,y∈L,则下列命题等价:
(1)(x,y)∈θ(I);
(2)(∃a∈I)x∨a=y∨a;
(3)(∃a,b∈I)(x∨a)∧b*=(y∨a)∧b*。
证明易得,(2)(3)。由定理5得,(1)(3)。
下证(3)(2)。设存在a,b∈I,使得(x∨a)∧b*=(y∨a)∧b*。因此((x∨i)∧b*)∨b**=((y∨a)∧b*)∨b**。
根据Stone代数运算的分配性及运算性质b*∨b**=1。所以x∨(a∨b**)=y∨(a∨b**)。又由定理1知,a,b**∈I,故a∨b**∈I,所以(2)成立。

定理5Ck(L)≅KI(L)。
证明由δI的定义得,R{0}=ω(相等关系)及RL=ι(泛同余关系)。先证对任意的I,J∈KI(L),有δI∧δJ=δI∧J。由定理2知,I∧J∈KI(L)。因为I∧J≤I,I∧J≤J,故由推论1知,δI∧J≤δI,δI∧J≤δJ,所以δI∧J≤δI∧δJ。
设(x,y)∈δI∧δJ,由文献[16]知,(x,y)∈δI且(x,y)∈δJ。因此存在i∈I,j∈J,使得x∨i=y∨i,x∨j=y∨j,于是有x∨(i∧j)=y∨(i∧j),又因i∧j∈I∧J,所以(x,y)∈δI∧J。故δI∧δJ≤δI∧J。所以δI∧δJ=δI∧J。
下证若I,J∈KI(L),有δI∨δJ=δI∨J。由定理2知,I∨J∈KI(L)。由于I∨J≥I,I∨J≥J,由推论1知,δI∨J≥δI,δI∨J≥δJ,所以δI∨J≥δI∨δJ。
设(x,y)∈δI∨J,则存在i∈I及i∈J,使得x∨i∨j=y∨i∨j,故
于是(x,y)∈δI∨δJ,因此δI∨J≤δI∨δJ,所以δI∨δJ=δI∨J。
由定理1的证明知,若δI=δJ当且仅当I=KerδI=KerδJ=J,从而映射I→δI建立起Ck(L)→KI(L)的对应,所以Ck(L)≅KI(L)。
3 结束语
理想是研究Ockham代数类的结构及同余关系的一个重要工具,特别是核理想,根据核理想的性质特征,使人们对抽象的相关Ockham代数类的结构及同余关系有一个清晰的认识,有助于了解双重Stone代数的结构,同时丰富了序代数结构的研究。
[1]BLYTH T S,VARLET J C.Ockham algebras.Oxford:Oxford University Press,1994.
[2]BLYTH T S,VARLET J C.On a common abstraction of de Morgan algebras and Stone algebras.Proc.Roy.Soc.Edinburgh,1983,94A:301-308.
[3]黎爱平.分配P-代数的核理想.赣南师范学院学报,2006(3):32-33.
[4]黎爱平,章书文.双重stone代数的素理想与同余关系.上饶师范学院学报,1999,19(6):12-15.
[5]方捷,吴丽云.拟补Ockham代数的理想与滤子.数学学报,2004,47(4):647-652.
[6]赵秀兰,刘洁.伪补MS-代数的核理想与同余关系.江西师范大学学报:自然科学版,2014,38(6):565-568.
[7]罗从文.MS-代数的核理想.应用数学,2001,14(1):39-41.
[8]张小红,刘三阳,刘用麟.伪MIL-代数(WPBL-代数)的正则滤子.西安电子科技大学学报:自然科学版,2006,33(5):829-832.
[9]方捷,沈吓妹.平衡半伪补Ockham代数的滤子.模糊系统与数学,2010,24(3):38-45.
[10]王雷波,方捷.双重伪补代数的假值理想的一点注记.纯粹数学与应用数学,2012,28(1):119-122.
[11]王雷波,方捷.几乎伪补格的核理想与W-理想.模糊系统与数学,2012,26(1):61-66.
[12]牛超群,吴洪博.BRo代数中的*理想及其诱导的商代数.江西师范大学学报:自然科学版,2013,37(3):221-224.
[13]赵秀兰,马红娟,初元红,等.双重半伪补de Morgan代数的滤子同余关系.模糊系统与数学,2015,29(4):19-26.
[14]朱怡权.双重stone代数的主同余关系.纯粹数学与应用数学,2006,22(4):520-525.
[15]陈杰.格论初步.呼和浩特:内蒙古大学出版社,1990.
[16]GRATZER G.Lattice Theory.New York:W.H.Freeman and Company,1971.
The Kernel Ideal on Double Stone Algebras
ZHAOXiulan1,CHENLijuan2
(1.Department of Mathematics and Physics,Huanghe Science and Technology College, Zhengzhou 450063,China;2.College of Science,Henan Institute of Engineering,Zhengzhou 451191,China)
The concept of kernel ideal on double Stone algebras is introduced. The expression of ideal congruence is constructed and the discrimination theorem of the kernel ideal is obtained. According to the operational characteristics and the principal congruence representation theory of double Stone algebras, some equivalent expressions of the double Stone algebras are obtained. It is proved that the set of kernel ideal is isomorphic to the set of the congruences with the kernel ideal. Based on the conclusion, a method for the study of the properties of the other Ockham algebras is provided, and the theory of ordered algebraic structures is enriched.
Stone algebras; dual Stone algebras; double Stone algebras; kernel ideal; congruence
2016-12-20
国家自然科学基金(11302072);河南省基础与前沿技术研究(152300410129)
赵秀兰(1982-),女,河南商水人,副教授,硕士,主要从事格论与序代数结构方面的研究,(E-mail)xiulanz@126.com
1673-1549(2017)01-0088-04
10.11863/j.suse.2017.01.17
O153.1
A

