核级设备结构中基体夹杂界面应力计算分析

罗家成, 罗娟, 孙磊

(中国核动力研究设计院， 成都610213)

核级设备结构中基体夹杂界面应力计算分析

罗家成, 罗娟, 孙磊

(中国核动力研究设计院， 成都610213)

基于复变函数方法，研究了在反平面载荷下核级设备结构中基体夹杂界面应力分布。利用基体和夹杂在界面处的位移和应力连续边界条件，推导得到含复应力函数系数的线性方程组，求解该方程组获得基体和夹杂的界面应力。通过数值计算结果表明：夹杂形状、基体与夹杂剪切模量比值对界面环向应力和界面径向应力均有影响，为核级设备结构设计及工程应用提供理论参考。

弹性基体与夹杂；反平面问题；界面应力；复变函数方法

引言

在核级设备结构中，基体夹杂两相结构如纤维增强、颗粒增强等弥散强化材料是一种应用广泛的材料体系，例如燃料颗粒的单质碳化硅包覆层结构、内外层均为碳化硅纤维增强复合材料而中间为金属层的包壳结构，以及金属基体微封装燃料和全陶瓷微封装燃料等。由于引入了增强相，极大地提高了核级设备结构的性能，由包覆燃料颗粒弥散在陶瓷基体中构成的全陶瓷微封装燃料，其碳化硅基体可提供超常的辐照稳定性、高热导率以及热力学稳定性。因此，对于这些基体夹杂结构的力学性能研究在核工程领域具有重要的理论及工程意义，其基体与夹杂两相界面处的应力随夹杂的形状及材料性能的变化规律对于核级设备结构的设计及工程应用可提供参考。

事实上，基体夹杂问题一直是固体力学关注的热点，自从Muskhelishvili[1]和Eshebly[2]关于椭圆夹杂和椭球夹杂的研究工作以来，关于基体夹杂的应力应变场研究已有许多成果。Gong和Meguid[3-4]研究了弹性椭圆夹杂在无限远处受到反平面和平面载荷问题，给出了弹性场的解；Shen[5]等研究了具有非完全接触界面椭圆夹杂的反平面问题；Gao和Noda[6]给出了压电介质内任意形状夹杂二维电弹性场的分析结果；利用边界积分方程，Dong和Lo[7]分析了反平面载荷下夹杂和裂纹之间的相互作用，计算了单个及多个椭圆夹杂和裂纹作用下的应力强度因子；Karoui等[8]研究了不可压缩超弹性两相材料的反平面剪切问题，给出了两相材料楔形顶点处弹性场的解；Chen[9-10]采用复变函数方法研究了椭圆夹杂以及共焦多层椭圆夹杂的Eshebly问题，推导出了本征应变的解。

以上研究一般采用级数展开法，给出基体和夹杂弹性体内的复应力函数，而对于界面应力分布并未给出详细的计算分析。本文采用复变函数方法，引入Faber级数研究了在反平面载荷下的基体夹杂界面应力问题，利用界面应力和位移边界条件获得含基体和夹杂复应力函数系数的线性方程组，通过数值计算得到具有不同形状夹杂的界面环向应力和界面径向应力分布，分析了夹杂形状和材料性能对界面应力的影响。

1 基本方程

图1 基体含任意形状夹杂示意图

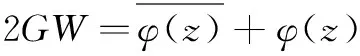
(1)

τ13-iτ23=φ′(z)

(2)

(3)

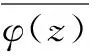
利用在边界Γ上的应力和位移边界条件可以求解得到φ(z)，进而可以获得基体和夹杂边界上的界面应力。

2 问题求解

对于图1 所示问题，由于在边界Γ上基体S1和夹杂S2完全接触，由应力和位移连续可得：

(4)

(5)

其中，μ=G2/G1，φ1(z)和φ2(z)分别为S1和S2内的未知复应力函数。

引入保角映射函数[1]：

(6)

式(6)将边界Γ外部S1区域保角映射到ζ平面上单位圆L1的外部，将ζ平面上的区域分别记为Ω1和Ω2，如图2 所示，其中R和mn为不同形状夹杂的系数。

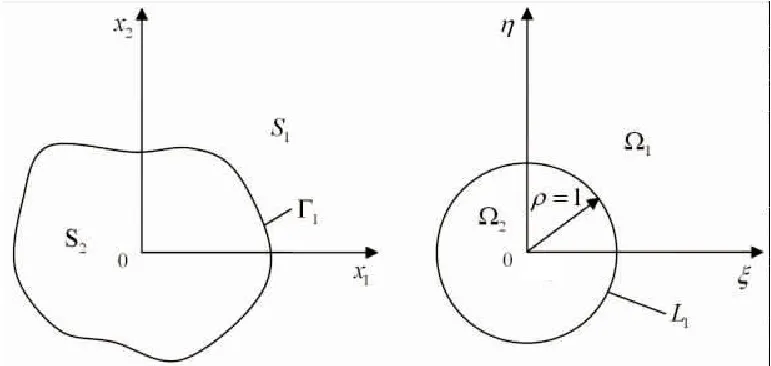
图2 保角映射示意图

在ζ平面上，将z=ω(ζ)代入式(4)和式(5)，则可以得到：

(7)

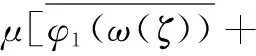
(8)

在区域Ω1和Ω2内的复应力函数分别可以表示为：

φ1(ω(ζ))=Bω(ζ)+φ10(ζ)

(9)

(10)

其中，

(11)

(12)

Pk(ω(ζ))为Faber级数[11]：

(13)

式中βk,n可由以下递推公式求得[11]：

β1,n=mn

(14)

(15)

将φ1(ω(ζ))和φ2(ω(ζ))代入式(7)和式(8)，并令ζ=eiθ=σ，可得：

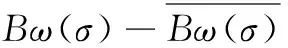
(16)

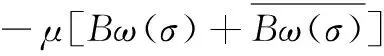
(17)

将φ10(σ),φ2(σ),ω(σ)代入(17)式，并比较等式两边σ±k(k≥1)的系数，整理可得：

(18)

(19)

(20)

(21)

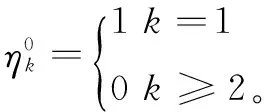
3 数值计算与分析

对于基体中含一圆形夹杂，保角映射函数可以表示为[12]：

z=ω(ζ)=Rζ

(22)

其中，R=a为圆形夹杂的半径。

图3 和图4 分别为圆形夹杂的界面径向应力和界面环向应力曲线，与文献[3]结果一致。圆形夹杂界面径向应力随着夹杂和基体剪切模量之比K的逐渐增大而递增，而界面环向应力随着剪切模量之比K的逐渐增大而减小。硬夹杂的界面径向应力大于软夹杂的界面径向应力，而硬夹杂的界面环向应力小于软夹杂的界面环向应力。

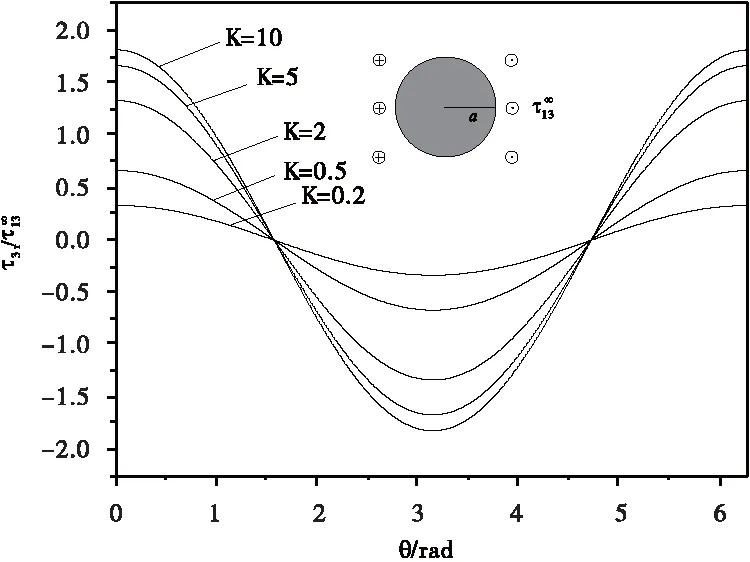
图3 圆形夹杂界面径向应力曲线

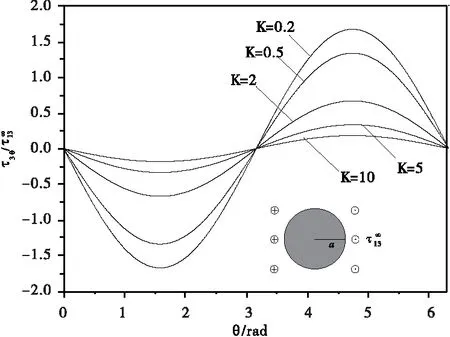
图4 圆形夹杂界面环向应力曲线

对于基体中含一椭圆形夹杂，保角映射函数可以表示为[12]：

z=ω(ζ)=R(ζ+mζ-1)

(23)

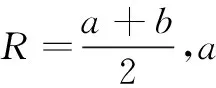
椭圆形夹杂的界面径向应力和界面环向应力曲线如图5 和图6 所示。硬夹杂的界面径向应力大于软夹杂的界面径向应力，并随着剪切模量之比K的逐渐增大而递增。界面环向应力与界面径向应力变化趋势相反，即硬夹杂的界面环向应力小于软夹杂的界面环向应力，且随着K增大而减小。

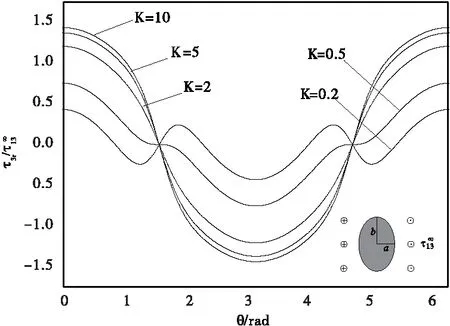
图5 椭圆夹杂界面径向应力曲线

图6 椭圆夹杂界面环向应力曲线

对于无限基体中含一正方形夹杂，保角映射函数可以表示为[12]：

(24)

其中，R=3a/5，a为正方形的边长。

图7 和图8 分别为正方形夹杂的界面径向应力和界面环向应力曲线。与圆形夹杂类似，硬夹杂界面径向应力大于软夹杂的界面径向应力并随着K递增，而硬夹杂的界面环向应力小于软夹杂的界面环向应力并随着K递减。界面径向应力和界面环向应力在正方形夹杂四个尖角处具有明显的应力集中。

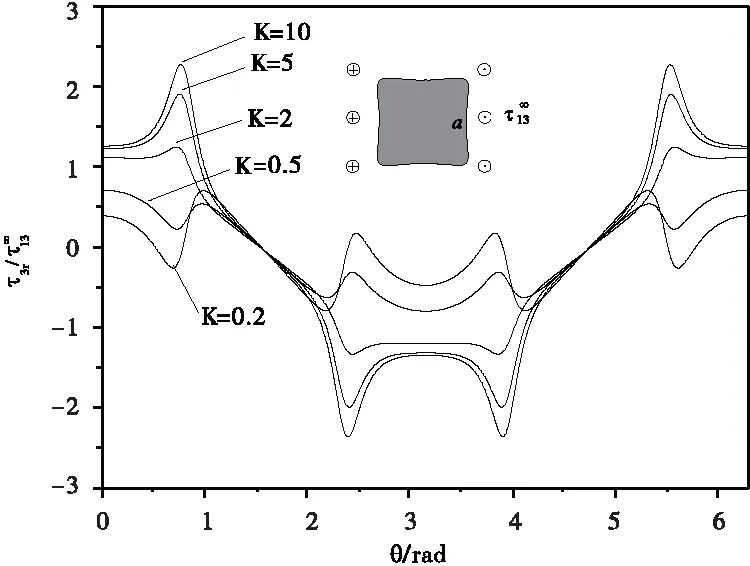
图7 正方形夹杂界面径向应力曲线

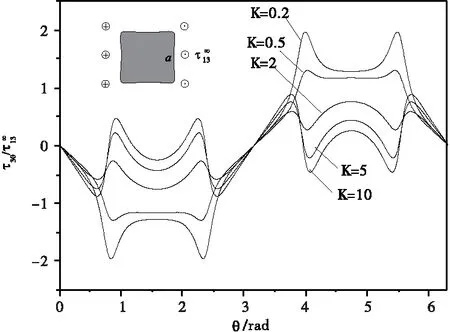
图8 正方形夹杂界面环向应力曲线

对于无限基体中含一等边三角形夹杂，保角映射函数可以表示为[12]：

(25)

其中，R=3a/5，a为三角形的边长。

图9 和图10 分别为三角形夹杂的界面径向应力和界面环向应力曲线。界面应力随K的变化与圆形夹杂类似，同样硬夹杂界面径向应力大于软夹杂，而硬夹杂的界面环向应力小于软夹杂的界面环向应力。三角形夹杂界面径向应力和界面环向应力在三个尖角处具有明显的应力集中，其中界面径向应力在0度角上应力最大，大于其他两个角；而界面环向应力在0度角上应力为零，应力集中在120度和240度角上。

对于具有其他任意形状的夹杂，只要给出公式(6)表征夹杂形状的保角映射函数，均可通过数值方法计算得到基体和夹杂的界面应力。

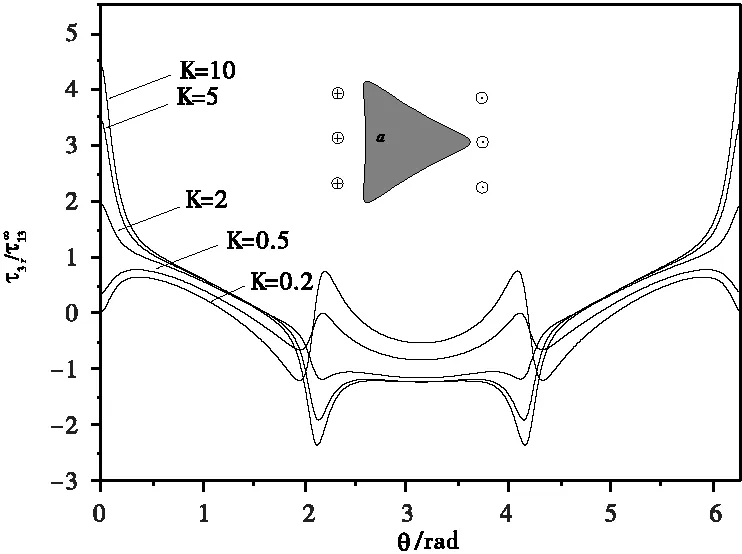
图9 三角形夹杂界面径向应力曲线

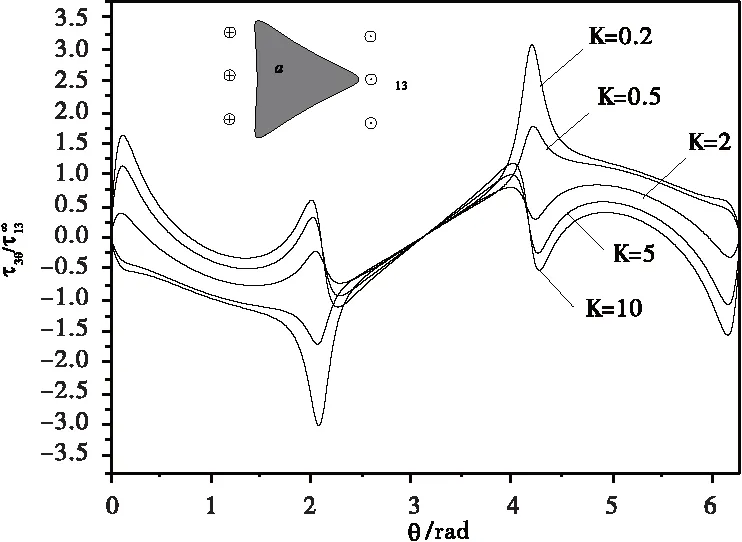
图10 三角形夹杂界面环向应力曲线

4 结束语

采用复变函数方法对基体含任意形状夹杂的界面应力进行了分析，通过数值计算表明：界面径向应力随着剪切模量之比的增大而递增，界面环向应力随着剪切模量之比的增大而递减；硬夹杂的界面径向应力大于软夹杂的界面径向应力，而硬夹杂的界面环向应力小于软夹杂的界面环向应力；正方形和三角形夹杂的界面应力在夹杂尖角上具有应力集中。本文的数值计算方法可为核级设备结构设计及工程应用中的界面应力分析提供一定的参考。

[1]MUSKHELISHVILI N I.Some basic problems of the mathematical theory of elasticity.Groningen:Noordhoff Ltd,1975.

[2]ESHELBY J D.The elastic field outside an ellipsoidal inclusion.Proc R Soc Lond A,1959,252:561-569.

[3]GONG S X,MEGUID S A.A general treatment of the elastic field of an elliptical inhomogeneity under antiplane shear.J Appl Mech,1992,59:131-135.

[4]GONG S X,MEGUID S A.On the elastic fields of an elliptical inhomogeneity under plane deformation.Proc R Soc Lond A,1993,443:457-471.

[5]SHEN H,SCHIAVONE P,RU C Q,et al.An elliptic inclusion with imperfect interface in anti-plane shear.Int J Solids Struct,2000,37(33):4557-4575.

[6]GAO C F,NODA N.Faber series method for two dimensional problems of an arbitrarily shaped inclusion in piezoelectric materials.Acta Mech,2004,171(1):1-13.

[7]DONG C Y,LO S H.An integral equation formulation of anti-plane inhomogeneities.Eng Anal Bound Elem,2013,37(11):1416-1425.

[8]KAROUI A,ARFAOUI M,TRIFA M,et al.The anti-plane shear elastostatic fields near the wedge vertes of an incompressible hyperelastic bimaterial.Int J Eng Sci,2015,97:6-17.

[9]CHEN Y Z.Closed form solution for Eshelby’s elliptic inclusion in antiplane elasticity using complex variable.Z Angew Math Phys,2013,64(6):1797-1805.

[10]CHEN Y Z.Solution of multiple confocally elliptical layers with dissimilar properties in antiplane elasticity with eigenstrains and remote loading.Appl Math Model,2016,40(7-8):4572-4585.

[11]KOSMODAMIANSKII A S,KALOEROV S A.Thermal stress in connected multiply plates.Kiev:Vishcha Shkola,1983:45-46.(in Russian)

[12]SAVIN G N.Stress concentration around holes.London:Pergamon Press,1961.

Numerical Analysis of Interface Stresses Between Matrix and Inclusion in the Structure of Nuclear Equipment

LUOJiacheng,LUOJuan,SUNLei

(Nuclear Power Institute of China, Chengdu 610213, China)

Based on the complex method, the interface stresses between matrix and inclusion in nuclear equipment under antiplane loadings are analyzed. By using the displacement and stress continuous conditions on the interface, the linear equations containing all the unknown coefficients of the complex potential are derived. Through numerical solving, the complex potentials and interface stresses of matrix and inclusion are finally obtained. It is found by the numerical calculation that the geometry and the shear modulus ratio of the matrix and inclusion both have influences on the interface radial and hoop stress, which can be a reference for the design and engineering application of the structure of nuclear equipment.

elastic matrix and inclusion; antiplane problem; interfacial stress; complex potential method

2016-03-31

罗家成(1984-),男,四川彭州人,助理研究员,博士,主要从事反应堆结构力学方面的研究,(E-mail)ljcnuaa@126.com

1673-1549(2017)01-0055-05

10.11863/j.suse.2017.01.10

O343

A