不同腹板嵌入方式模拟对波形钢腹板组合箱梁建模精度的影响

刘欢

（铁道第三勘察设计院集团有限公司，天津市 3 00142）

不同腹板嵌入方式模拟对波形钢腹板组合箱梁建模精度的影响

刘欢

（铁道第三勘察设计院集团有限公司，天津市 3 00142）

为探究不同腹板嵌入方式模拟对波形钢腹板组合箱梁建模精度和效率的影响，利用ANSYS建立三种连接方式下的有限元模型，分析其在荷载作用下的挠度、应力、剪力滞效应和自振频率，并将有限元模拟结果与现场模型试验实测数据对比，以找出最符合实际的连接方式。结果表明，MPC方式的建模效率明显高于共节点式与嵌入式，且能够满足精度要求，是最符合实际腹板嵌入连接的方式。该研究可为波形钢腹板组合箱梁有限元仿真提供参考。

波形钢腹板；剪力连接件；有限元模拟；试验对比

0 引 言

波形钢腹板组合结构桥梁起源于法国，在日本得到广泛应用，因具有梁体整体重量较轻，抗震性能好，预应力的施加效率高，腹板抗剪性能优越，耐久性好，有良好的视觉美感等诸多优点[1]而被设计师门所青睐，具有广阔的发展前景。波形钢腹板组合箱梁近年来的研究多以静力学性能研究为主[2-5]，且研究手段多以变分推导、有限元仿真和模型试验为主。如何保证建模精度和效率，同时解决研究中出现有限元建模和实际试验结果存在较大偏差的问题，值得研究人员和设计人员深入思考。

本文采用有限元分析与模型试验相结合的方法对波形钢腹板嵌入顶、底板方式进行研究，对比三种连接方式下模型的力学性能，从而选取出一种最为合理且接近实际情况的剪力连接件模拟方式，为后续研究人员利用有限元软件建立波形钢腹板组合箱梁模型提供有效借鉴和技术支持。

1 腹板嵌入连接方式研究

一般来说，波形钢腹板与混凝土上、下翼板的连接采用以下4种连接方式[6]：（1）嵌入型连接；（2）角钢剪力键连接；（3）双开孔钢板连接键连接（Twin-PBL连接）；（4）单开孔钢板与栓钉的并用连接（S-PBL连接+栓钉连接）。在通常的有限元模拟中，顶、底板（混凝土板）采用Solid单元模拟，波形钢腹板采用Shell单元模拟，由于这两种单元具有不同的自由度[7]，所以在腹板嵌入时存在模拟精度误差和计算效率较低的问题。解决这一问题，通常的有限元模拟手段有三种（见图1）。

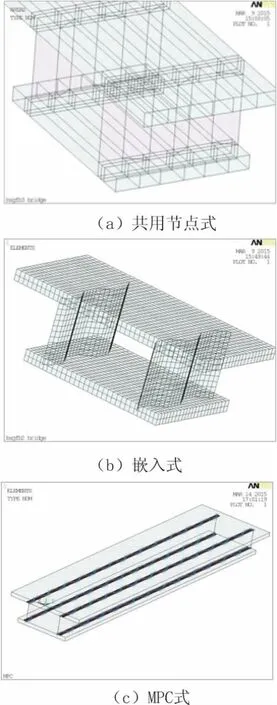
图1 三种嵌入方式的有限元模拟

2 模型试验

本次试验梁采用的腹板嵌入方式是目前使用最广泛的嵌入型与栓钉并用连接的方式（见图2），嵌入深度为55 mm，桥纵向的抗剪作用主要靠斜幅间的混凝土块（亦称抗剪齿键）与桥横向贯通钢筋来共同承担；横隔板和腹板以及顶底板连接采用卡槽连接，后期用粘接剂连接到一起形成整体。

图2 模型试验梁使用的嵌入型与栓钉并用的连接方式

集中加载：利用反力架加载跨中集中荷载，并反复加载三次。作用点为波形钢腹板箱梁的上翼板与波形钢腹板交界处，每一处作用位置力的大小为15 kN，分三级加载。

均布加载：通过堆放砖块实现全跨均布加载，总的加载为36 kN，分三级加载。

挠度测点：选取试验梁1/4、1/2、3/4跨截面和端支座处进行挠度测试，在箱梁底板布置挠度测点。

应变测点：选取试验梁1/4、1/2、3/4跨截面进行应变测试，在顶板、底板和腹板均布置应测点。

自振频率测点布置：在试验梁1/4、3/4跨和端支座处布置竖向拾振器、1/2跨截面布置竖向和横向拾振器采集试验梁竖向以及横向振动并进行模态分析，采用频率范围200 Hz。

3 试验结果分析

3.1 挠度

建立有限元模型，对比共节点式、嵌入式、MPC式三种模拟顶底板与波形钢腹板连接形式所建模型的参数化分析结果，提取三种不同建模方式的波形钢腹板简支梁模型在分三级加载作用下跨中截面的竖向挠度，并与模型试验梁实测值进行对比，对比结果如图3所示。

由上述对比可知，在跨中集中荷载分级加载下，三种不同建模方式下的波形钢腹板组合箱梁跨中截面的挠度基本呈线性增长趋势，这一点都与实际情况吻合。集中荷载下嵌入式误差最大高达19.2%，共节点式误差最大值为11.7%，MPC方式最大误差约为4.4%。均布荷载下嵌入式误差最大高达7.0%，共节点式误差最大值为10.5%，MPC方式误差约为3.5%。但是相对于共节点式以及嵌入式，MPC式的挠度值更接近于实测结果。

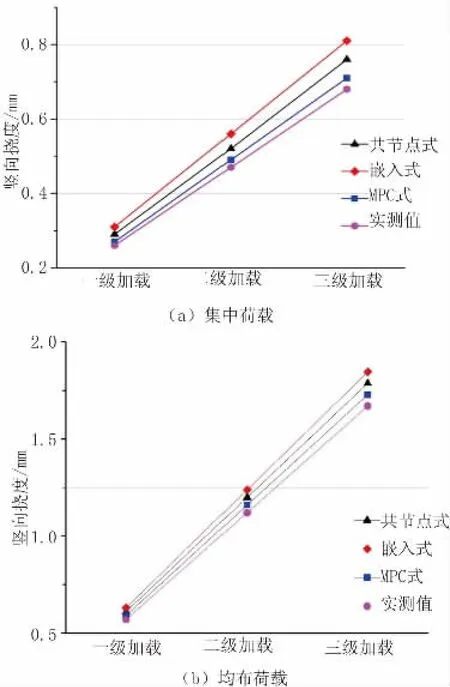
图3 有限元分析跨中挠度值与实测挠度值对比

3.2 应力及剪力滞系数

试验梁在荷载作用下，顶底板纵向正应力沿箱梁横向分布规律为靠近腹板位置最大，远离腹板位置较小，随着加载等级的上升，顶底板的应力值呈线性上升态势，波形钢腹板高度范围内的应变值几乎为零，可忽略波形钢腹板对箱梁纵向抗弯的贡献。离支座位置较近距离处箱梁截面顶、底板存在剪力滞现象，且剪力滞效应对挠度及自振频率有一定影响[1]。

剪力滞效应大小常用剪力滞系数来表征，提取三种不同建模方式下的波形钢腹板简支梁模型在集中荷载2级加载作用下1/2跨处截面的顶、底板纵向正应力数据，并绘制其沿箱梁宽度方向的剪力滞系数变化规律，同时与波形钢腹板简支试验梁的实测剪力滞系数变化规律进行对比。数据对比如图4、图5所示。

根据图4、图5所示，显示出顶、底板剪力滞效应呈现靠近腹板区域的剪力滞系数最大，中心线处较小的正剪力滞现象。在跨中集中荷载作用下，根据上述三种混凝土顶底板与波形钢腹板连接方式模拟所建模型的相关截面剪力滞系数与实测剪力滞系数的对比结果可知，总体而言，三种建模方式的剪力滞系数趋势都与实测结果一致，对比代表性位置的具体数值结果，MPC式的剪力滞系数更为接近实测结果，嵌入式次之，共节点式稍大，在均布荷载下有相似的规律。值得注意的是，集中荷载下腹板交界面处最大剪力滞系数大于均布荷载作用下剪力滞系数，在设计上应引起设计人员重视。

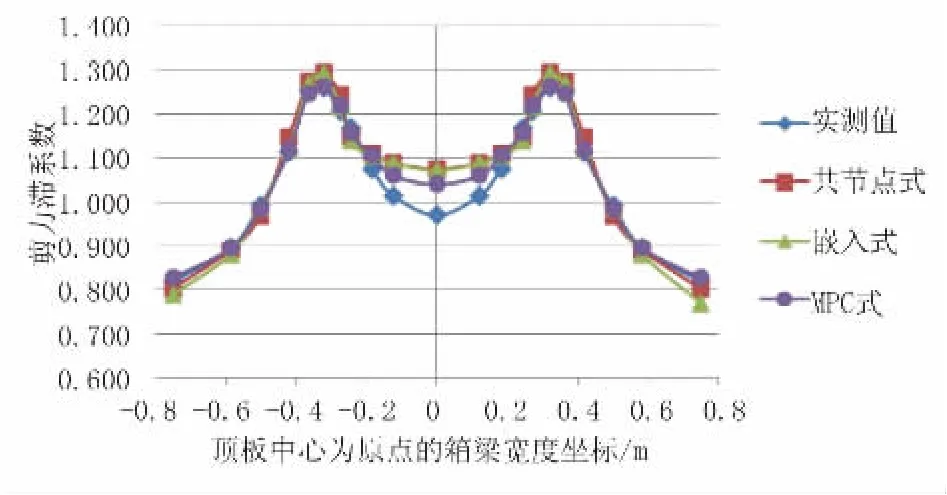
图4 工况一2级加载作用下模型1/2跨截面顶板剪力滞系数分布对比图

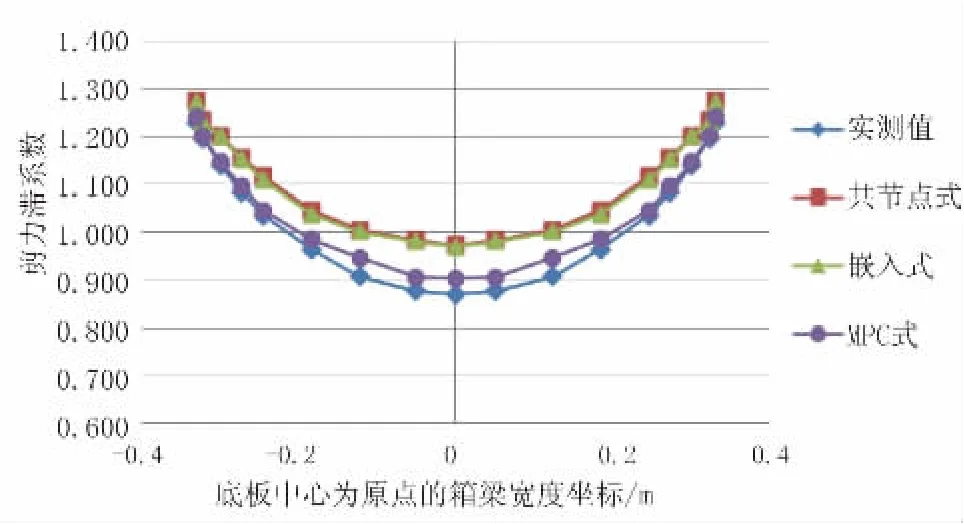
图5 工况二3级加载作用下模型1/2跨截面顶板剪力滞系数分布对比图

3.3 自振频率

根据三种不同连接方式所建试验梁模型的模态分析结果，将竖向弯曲前两阶频率与实测结果进行对比（见表1）。

根据表1对比结果可知，三种不同模拟连接件建模方式的模态分析结果的一阶频率都与实测值差距不大，当阶数增大时，相比之下MPC式建模方式模型的结果与实测值差距最小，误差仅为2.6%，嵌入式次之，共节点式稍大。

4 结论

通过三种不同模拟方式分别建立波形钢腹板简支梁与连续梁有限元模型，对其静动力特性进行模拟计算，并与实测试验梁结果进行对比。分析结果表明，三种建模方式都与实测值吻合良好，再次验证了这三种建模方式的正确性。然而，对于建模效率而言，MPC方式的建模效率明显高于共节点式与嵌入式。所以在满足精度要求的情况下，MPC建模方式为最优选择。

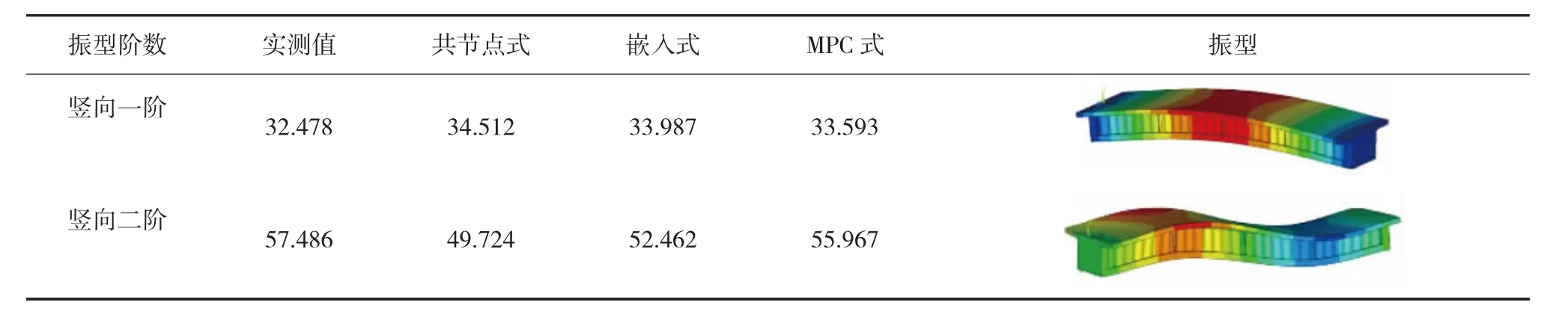
表1 波形钢腹板简支梁竖向弯曲振动频率对比 Hz

[1]冀伟.波形钢腹板组合箱梁桥的力学性能分析与试验研究[D].兰州：兰州交通大学,2013.

[2]吴文清,叶见曙,万水,等.波形钢腹板-混凝土组合箱梁截面变形的拟平截面假定及其应用研究 [J].工程力学,2005（5）: 177-180，198.

[3]李宏江,叶见曙,万水，等.波形钢腹板箱梁横隔板间距的研究[J].公路交通科技,2004（10）:51-54.

[4]M.Basher,N.E.Shanmugam,A.R.Khalim.Horizontally curved composite plate girders with trapezoidally corrugated webs[J]. Journal of Constructional Steel Research,2011,（67）:947-956.

[5]王圣保.波形钢腹板PC组合箱梁抗扭性能试验[J].建筑结构,2012,42(9):121-125.

[6]陈宜言.波形钢腹板预应力混凝土桥设计与施工[M].北京:人民交通出版社,2009．

[7]王新敏，ANSYS工程结构数值分析 [M].北京：人民交通出版社，2013.

[8]周艳,高耀东.利用MPC技术对SOLID和SHELL单元进行连接[J].内蒙古科技大学学报,2011,30(3):241-243.

U441

A

1009-7716（2017）01-0137-03

10.16799/j.cnki.csdqyfh.2017.01.040

2016-12-06

国家自然科学基金项目（51368032）

刘欢（1990-），男，甘肃陇南人，助理工程师，从事桥梁工程设计工作。