对基于标志点的颅面部三维影像重叠方法的改进及新的上颌骨三维影像重叠方法

翁 瑶，王紫仪，张晓东

(沈阳军区总医院口腔内科，辽宁 沈阳 110840)

对基于标志点的颅面部三维影像重叠方法的改进及新的上颌骨三维影像重叠方法

翁 瑶，王紫仪，张晓东*

(沈阳军区总医院口腔内科，辽宁 沈阳 110840)

目的 优化现有的基于标志点的三维影像重叠方法，并在此基础上提出一种更为简便的用以重叠上颌骨三维影像方法。方法 对9名志愿者均间隔1年拍摄2幅锥形束CT(CBCT)影像，比较两种数学运算方法(6点优化法和8点优化法)对建立ELSA共坐标系误差的优化效果。以前后鼻棘点(ANS、PNS)建立用以重叠上颌骨的共坐标系(ANS、PNS共坐标系)。挑选数个标志点检测影像的重叠误差，并进行统计学分析。结果 在未优化、6点优化、8点优化3种方法中，ELSA共坐标系建立的平均线距和角度误差分别为(0.60±0.47)mm和(0.49±0.38)°、(0.44±0.39)mm和(0.48±0.37)°、(0.41±0.34)mm和(0.41±0.32)°，8点优化法对ELSA共坐标系建立的平均线距误差小于无优化和6点优化法(P<0.05)。ELSA共坐标系下各标志点重叠的平均线距和角度误差分别为(0.95±0.50)mm和(1.06±0.65)°、(0.92±0.54)mm和(0.92±0.58)°、(0.80±0.43)mm和(0.87±0.59)°，3种方法差异有统计学意义(P均<0.000 1)。经8点优化后，在ELSA、ANS、PNS共坐标系中用以重叠上颌骨的各标志点的平均线距和角度误差分别为(0.92±0.47)mm和(1.14±0.66)°、(0.99±0.47)mm和(1.33±0.64)°、(1.00±0.62)mm和(1.08±0.70)°。结论 本研究提出的8点优化法可显著提高ELSA共坐标系的准确性，且所提出的上颌骨三维影像重叠方法的误差已基本达到进行临床病例分析的要求范围。

锥形束计算机体层摄影术；三维头影重叠；优化；算法；头影测量学

在正畸和口腔其他领域，锥形束CT(cone-beam computed tomography， CBCT)的应用已经越来越普及[1]。CBCT可用于三维头影测量分析、上气道和颞下颌关节的测量、评估牙体牙髓的病变和埋伏牙等，三维头影重叠可测量颅骨生长发育以及预测治疗效果[2-3]。由于人为确定解剖标志点的误差对重叠的准确性产生极大的影响[4]，目前优化此方法主要是通过增加额外标志点(控制点)并假定其位置在生成的坐标系中不变而实现[5-7]。目前，使用基于标志点的重叠方法进行临床分析的研究较少，本研究对基于标志点的重叠方法进行优化，并在此基础上提出一种更为简便的重叠上颌骨三维影像的方法。

1 资料与方法

1.1一般资料 2015年2月—2016年2月间招募9名志愿者，其中男2名，女7名，年龄24～51岁，平均(28.9±8.6)岁。所有志愿者均间隔1年接受2次锥形束CT检查(T1、T2)。

1.2 仪器与方法 采用KaVo iCat CBCT机，管电压120 kV，管电流5 mA，曝光时间8.9 s，层厚0.3 mm，FOV 232 mm×170 mm，灰度值14位，图像采集单次旋转360°，图像输出格式DICOM 3.0。由同1名具有专业资格且经验丰富的放射科医师操作。

1.3 基于解剖标志点的三维头影重叠方法

1.3.1 解剖标志点 本研究使用的各解剖标志点如下：左右棘孔(Fs_L、Fs_R)及其中点(ELSA)；左右侧耳点(Po_L、Po_R)；枕骨大孔后缘点(DFM)；左右卵圆孔点(LFO、RFO)；左右眶下孔点(IO_L、IO_R)；前鼻棘点(ANS)；后鼻棘点(PNS)；鼻根点(N)；颅底点(Ba)；切牙孔后缘点(Ifn)；左右颏孔点(Mf_L、Mf_R)；左右髁突内侧极点(MPC_L、MPC_R)；左右髁突外侧极点(LPC_L、LPC_R)；左右下颌小舌点(Li_R、Li_L)；上颌左右腭大孔前缘点(GPF_L、GPF_R)。由同1名医师采用InVivo5软件(Anatomage, San Jose, CA)于同一屏幕上同时对T1、T2两幅三维影像的解剖标志点进行定位。

1.3.2 建立ANS和PNS共坐标系 在ELSA共坐标系[4]的基础上建立用以重叠上颌骨的ANS和PNS共坐标系。ANS共坐标系的建立：首先根据Lagravère等[4]的方法建立ELSA共坐标系，然后在ELSA共坐标系的基础上将所有标志点的坐标减去点ANS的坐标，从而将ELSA共坐标系平移至以解剖标志点ANS为原点的坐标系。如果有n个标志点，则坐标系平移后每个标志点坐标的计算方法为：

(1)

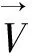
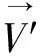
(2)

其中矩阵[A1]为：

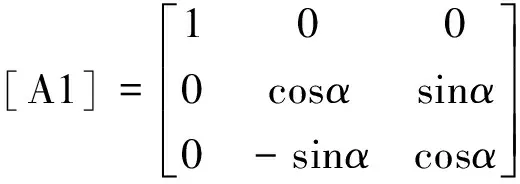
(3)

角使用坐标系旋转前的点PNS：

(4)

脚标x、y、z表示相应的坐标轴，并经以下运算获得角

(5)

以上即为第1次坐标系旋转。然后，以第1次旋转后的坐标系的z轴为旋转轴再次旋转坐标系，使点ANS的x轴坐标为零，第2次旋转后的点PNS以下式表示：

(6)

矩阵[A2]为：

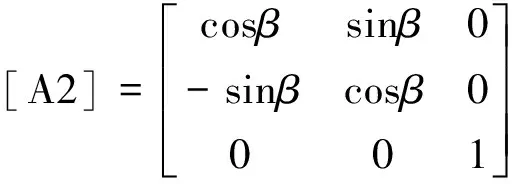
(7)

角使用第1次坐标系旋转后的点PNS：

(8)

脚标x、y、z表示相应的坐标轴，并经以下运算获得

(9)

这两步的坐标系旋转可被应用于任一原ELSA共坐标系下的标志点，其式如下

(10)

上式中j表示第n个解剖标志点。

经2次坐标系旋转后，即成功建立用以重叠上颌骨的ANS共坐标系。PNS共坐标系的建立与ANS共坐标系的建立基本相同，以PNS作为坐标系的原点。

1.4 对既往6点优化法的改进 为校正人为定点误差，DeCesare等[3]于2013年提出了6点优化法，其原理为对多个目标函数的最优化问题进行求解，以求出T2图像中的点Po_L、Po_R和DFM的校正向量。这些目标函数分别为：①Po_L、Po_R、DFM之间及与RFO和LFO之间的相对距离；②Po_L、Po_R、DFM之间及与RFO和LFO之间的相对角度。而本研究提出的8点优化法即在上述6点优化法的基础上额外增加两个控制点(IO_L和IO_R)，如此文献中的6点优化法即变为：

(11)

关于δuPo_L、δuPo_R、δuDFM的函数

(12)

边界：(-5, -5, -5) < δuPo_L< (5, 5, 5)

(13)

(-5, -5, -5) < δuPo_R< (5, 5, 5)

(14)

(-5, -5, -5) < δuDFM< (5, 5, 5)

(15)

上式中fi指公式(11)的最优化问题中的主要目标函数；gi指公式(11)的最优化问题中的次要目标函数；δuPo_L、δuPo_R、δuDFM分别为Po_L、Po_R、DFM的校正向量，用以设置T2图像的坐标系；wf,i为fi的权重系数；wg,j为gi的权重系数。权重系数的分配基于目标函数的重要性且满足公式(16)：

(16)

(17)

(18)

(19)

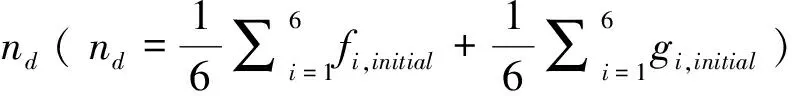
1.5坐标系有效性的测量

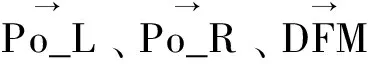
1.5.2 测量三维图像的重叠误差 在ELSA、PNS、ANS共坐标系中分别计算以下参数：①计算各标志点在T1和T2图像间的欧氏距离，并取其平均值作为ELSA共坐标系下三维图像重叠的平均线距误差；②计算各标志点连线在T1和T2图像中的角度，并取其平均值作为各共坐标系下三维图像重叠的平均角度误差；③计算在不同优化方法下(6点优化法、8点优化法)各坐标系中(ELSA共坐标系、PNS共坐标系、ANS共坐标系)T1、T2图像间各标志点在各坐标轴(x,y,z)上的差异。

1.7试验流程 ①在InVivo5软件中对9组样本进行解剖标志点定位；②将9组样本标志点的坐标数据导入Excel软件，并在Excel软件中进行ELSA共坐标系的转换运算；③将ELSA坐标系转换运算的结果导入Matlab软件中进行优化算法的运算；④将优化算法的运算结果再次导入Excel软件，完成优化后的坐标系转换运算，同时计算各优化方法下各坐标系的建立误差和图像重叠误差；⑤采用SPSS软件中完成统计分析。本研究中坐标系转换的运算均采用Excel软件，不需图形化的操作。

2 结果

2.1 ELSA共坐标系的建立误差(表1) 未优化、6点和8点优化法建立ELSA共坐标系的平均线距误差的差异有统计学意义(P<0.02)，但6点和8点优化方法间差异无统计学意义，8点优化法平均线距误差小于未优化时(P<0.05)，从(0.60±0.47)mm降低至(0.41±0.34)mm。未优化、6点和8点优化方法对ELSA共坐标系建立的平均角度误差差异无统计学意义(P>0.06)。采用6点优化法后，Mf_L、Mf_R、Ba的平均角度误差均增大，只有N点的平均角度误差减小。而采用8点优化法时，所有检测点的平均线距误差和平均角度误差均减小。各标志点在T1、T2图像间各坐标轴的差异见图1。8点优化法效果示例见图2。

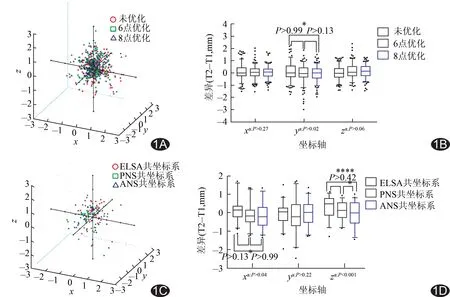
图1 各标志点在T1、T2图像间各坐标轴的差异 A.ELSA共坐标系下所有标志点在各坐标轴上差异的三维散点图； B.图1A数据的箱式图； C.采用8点优化法后，上颌骨各标志点在各坐标系中坐标轴差异的三维散点图； D.图1C数据的箱式图 (箱式图的上、下界分别为95%分位数和5%分位数，箱体的上、下界分别为1/4分位数和3/4分位数，箱体中的横线为均值；a：Friedman检验的结果；连线表示两两比较Dunn's检验的结果；*：P<0.05；**：P<0.01；***：P<0.001；****：P<0.000 1)

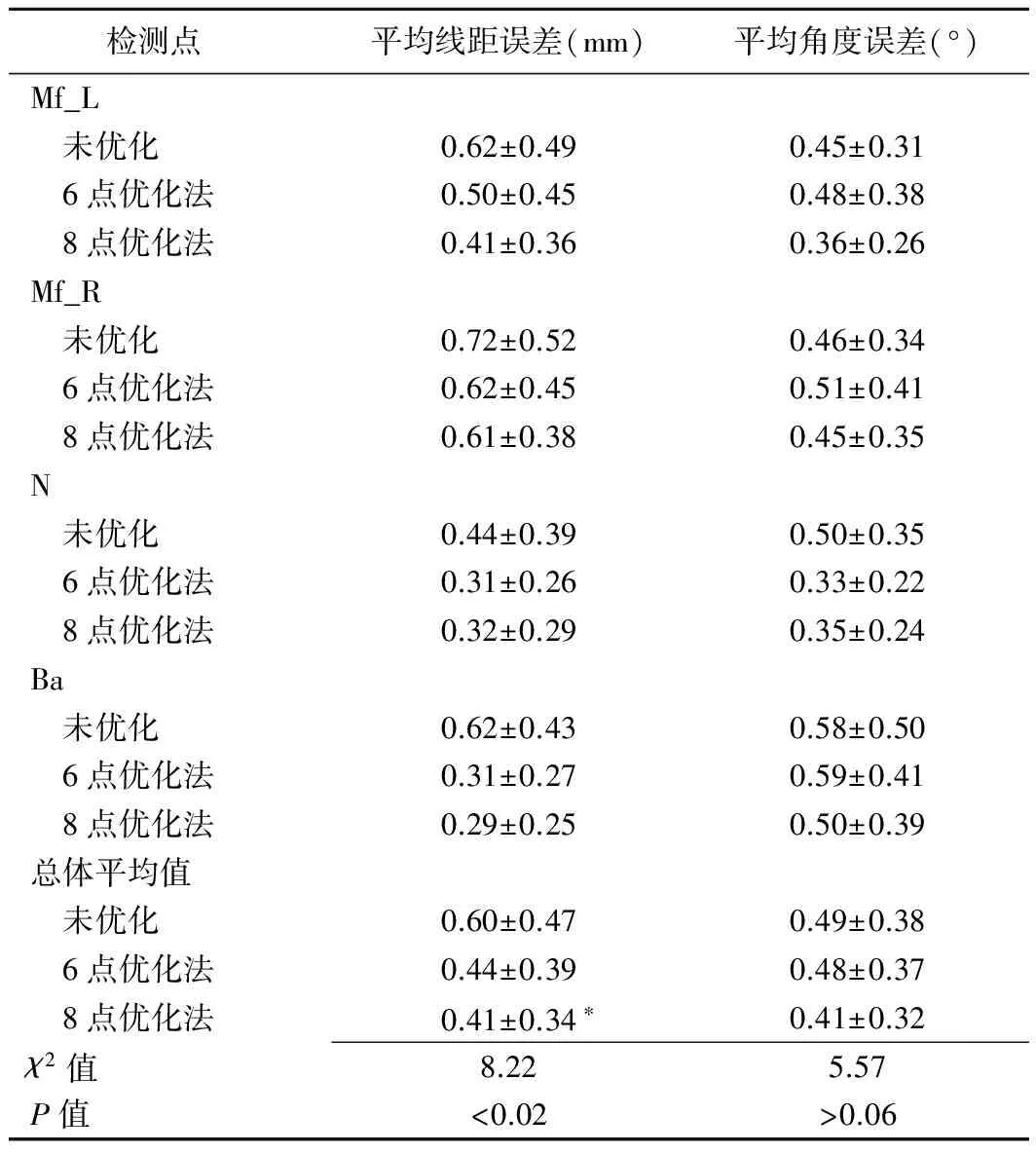
检测点 平均线距误差(mm)平均角度误差(°)Mf＿L 未优化0．62±0．490．45±0．31 6点优化法0．50±0．450．48±0．38 8点优化法0．41±0．360．36±0．26Mf＿R 未优化0．72±0．520．46±0．34 6点优化法0．62±0．450．51±0．41 8点优化法0．61±0．380．45±0．35N 未优化0．44±0．390．50±0．35 6点优化法0．31±0．260．33±0．22 8点优化法0．32±0．290．35±0．24Ba 未优化0．62±0．430．58±0．50 6点优化法0．31±0．270．59±0．41 8点优化法0．29±0．250．50±0．39总体平均值 未优化0．60±0．470．49±0．38 6点优化法0．44±0．390．48±0．37 8点优化法0．41±0．34∗0．41±0．32χ2值8．225．57P值<0．02>0．06

注：*：与未优化比较P<0.05

2.2 三维图像的重叠误差

2.2.1 平均线距误差 不同优化方法ELSA共坐标系各标志点的平均线距误差见表2。未优化、6点优化和8点优化在ELSA共坐标系下的平均线距误差为(0.95±0.50)mm、(0.92±0.54)mm、(0.80±0.43)mm，差异有统计学意义(χ2=56.80，P<0.000 1)。采用8点优化法评价上颌骨重叠的标志点在ELSA、ANS、PNS共坐标系的平均线距误差见表3。ELSA、ANS、PNS共坐标系的平均线距重叠误差分别为(0.92±0.47)mm、(0.99±0.47)mm、(1.00±0.62)mm，差异无统计学意义(χ2=2.84，P>0.24)。

2.2.2 平均角度误差 不同优化方法ELSA共坐标系各标志点的平均角度误差见表4。未优化、6点优化和8点优化在ELSA共坐标系下各标志点重叠的平均角度误差分别为(1.06±0.65)°、(0.92±0.58)°、(0.87±0.59)°，差异有统计学意义(χ2=26.70，P<0.0001)。采用8点优化法评价上颌骨骨重叠的标志点在ELSA、ANS、PNS共坐标系的平均角度误差见表5。PNS共坐标系的平均角度重叠误差[(1.08±0.70)°]小于ANS共坐标系[(1.33±0.64)°]，差异有统计学意义(χ2=7.81，P<0.02)；PNS与ELSA[(1.14±0.66)°]、ANS与ELSA共坐标系之间平均角度误差差异均无统计学意义(P均>0.05)。

3 讨论

目前，两种三维头影重叠方法分别为基于体素的重叠方法[2,8-9]和基于解剖标志点的重叠方法[4,6-7]。基于体素的重叠方法是使用计算机技术自动重叠参照结构，之后计算目标结构中所有像素点的位置差异，并用不同的颜色加以标示，最终生成一幅色谱图以显示骨的位置变化。

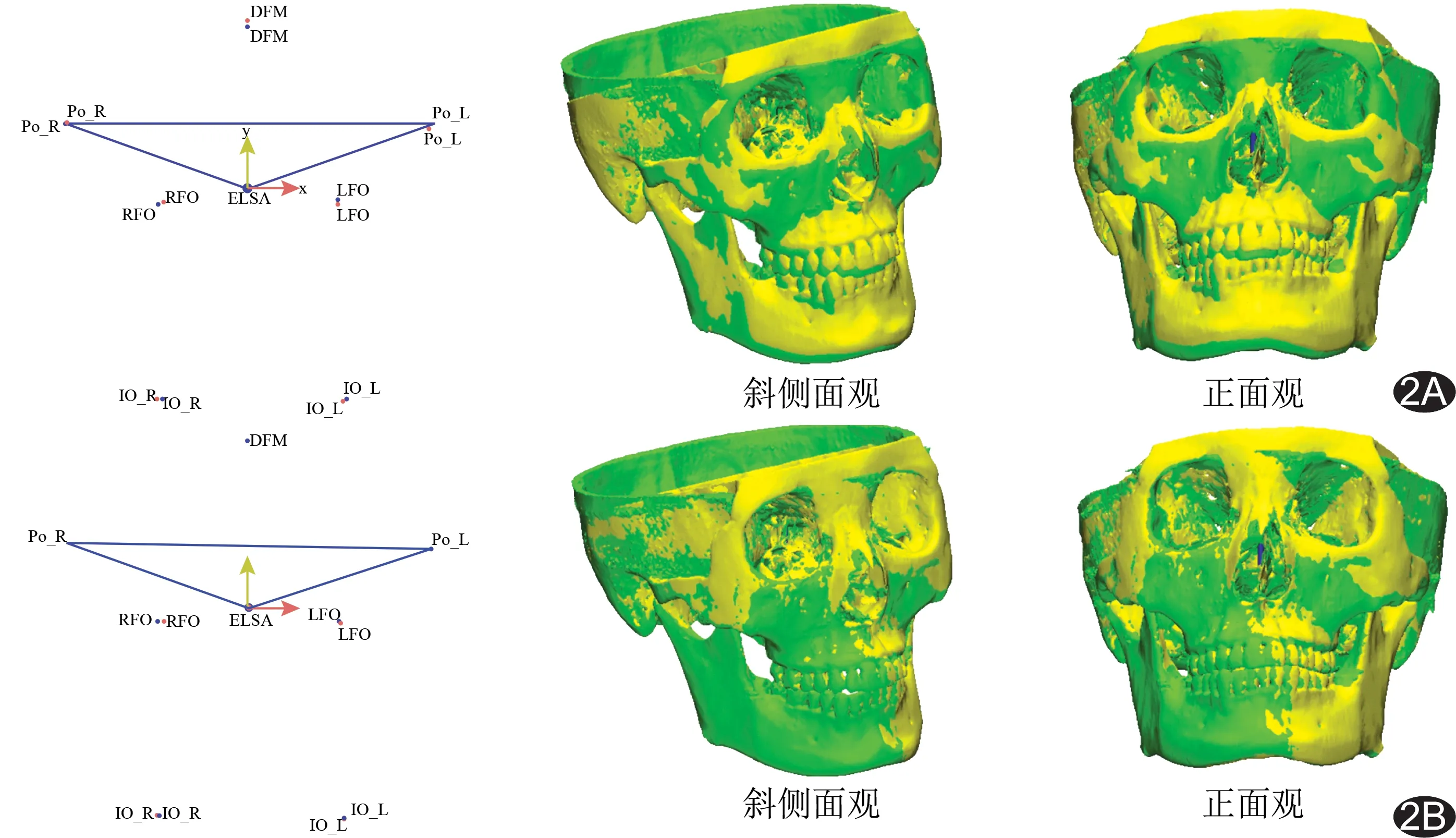
图2 8点优化法效果示例 A.ELSA共坐标系未优化时图像的重叠情况； B.采用8点优化法优化ELSA共坐标系后图像的重叠情况 (绿色和黄色影像的拍摄间隔1年，蓝色标志点来自绿色影像，红色标志点来自黄色影像

目前基于体素的重叠方法已大量应用于临床资料分析，并显示其较高的准确性。理论上该方法可彻底消除测量者的操作误差[10-12]。而基于标志点的重叠方法则是利用解剖标志点所确定的平面来重叠图像，与传统的二维重叠方法相似，因此更易被正畸医师们接受[3]。其原理为使用一系列定义明确的解剖标志点确定两个相互垂直的平面，并以此生成一个共同的三维直角坐标系[4]。其主要缺陷是测量者的定点误差会

影响影像重叠的准确性[7]，因而需要复杂的数学算法进行优化[3,7]，并且对标志点有很高的要求，如定位稳定、位置不受生长发育影响等[3,13]。目前，使用基于标志点的重叠方法的研究[5]较少，本研究对基于标志点的重叠方法进行优化，并在此基础上提出一种更为简便的三维上颌骨重叠方法。

3.1 各优化方法的效果评价 本研究发现在未应用优化方法时，ELSA共坐标系建立的平均线距误差仅(0.60±0.47)mm，与DeCesare等[3]的研究结果相差较大[(1.64±0.62)mm]，可能是由于本研究中实验者同时在前后两幅CT图像上同时定点所致。6点优化法并未显著改善坐标系的建立误差，8点优化法在优化坐标系建立的线距误差时与其他2种方法差异有统计学意义(P<0.05)。8点优化法对影像重叠的角度误差的优化效果[(0.87±0.59)°]优于6点优化法[(0.92±0.58)°]。同时，仅8点优化法对各标志点y轴误差的优化差异有统计学意义(图1B)，且8点优化法后各坐标轴上的误差范围更小(<±2 mm)。根据DeCesare等[3]优化方法的原理，控制点越多其优化效果越好，但同时更多的控制点将包含更多的人为定点误差，所以其数量势必存在一个均衡点，本研究结果提示采用4个控制点为最优选择。

表2 不同优化方法ELSA共坐标系下(19个点)的平均线距误差(mm， ±s)

表3 8点优化法三维影像重叠(用以评价上颌骨重叠的标志点)在不同坐标系的平均线距误差±s)

表4 不同优化方法ELSA共坐标系下(14个角)的平均角度误差(°， ±s)

注：*：与未优化比较,P<0.05；**：与未优化比较,P<0.000 1

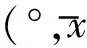
表5 8点优化法三维影像重叠(用以评价上颌骨重叠的角)在不同坐标系的平均角度误差±s)

注：*:与ANS坐标系比较,P<0.05

本研究中，采用8点优化方法后，用以建立坐标系的4个点基本上完全重合，而控制点中只有RFO点的重叠误差较大(图2)，可能是由于其本身的定点误差所致，所以哪种控制点的组合对优化的效果最好，也有待进一步研究。

3.2 ELSA共坐标系下图像的重叠误差 Lagravère等[14]认为，标志点识别的平均误差<1 mm即可被临床认可应用，误差为1～2 mm则可谨慎地用于各种头部影像分析中，如果误差>2 mm则认为此标志点的识别度很差而不可应用于临床。本研究的结果显示，经8点优化方法后，在ELSA共坐标系中，ANS和PNS的平均线距误差和平均角度误差均小于1 mm和1°，为使用此2点建立用以重叠上颌骨三维影像的坐标系提供了足够的支持。此外，在PNS和ANS共坐标系下各标志点的线距及角度误差基本在1 mm和1°左右，提示本研究提出的重叠上颌骨的方法可谨慎用于临床病例的各种头部影像分析。

本研究发现，在ELSA共坐标系下，点MPC_L、MPC_R、LPC_L、LPC_R及其连线MPC_L—MPC_R、LPC_L—LPC_R均有良好的稳定性和精确性。但Uzel等[15]采用与上述类似的方法测量髁突位置并与髁突记录仪的结果对比，结果表明该CBCT方法在测量髁突位置时准确性不佳。Uzel等[15]使用的测量方法(首先在三维影像数据中选取几个作为参照的解剖标志点，之后通过这些点来确定一个或多个二维的工作平面，最后在这个或这些工作平面进行二维测量)，不仅丢失了三维数据中的大量信息，而且在这些研究中用来确定工作平面的解剖结构为一些定义不明确的标志点(如最突点、最凹点等光滑骨表面的结构)，增大了测量误差。本研究采用的点MPC_L、MPC_R、LPC_L、LPC_R的定义相对明确，且其定位也不需要周围比较模糊的关节窝中的解剖结构辅助。Lemieux等[13]使用颅骨标本进行CBCT研究，发现点Li_R、Li_L在三维影像上的定位与干颅骨上的实际位置相差较大(空间位置误差>1 mm)，但本研究显示点Li_R、Li_L的定位稳定、可靠，若不考虑影像上此点与实际解剖结构的差异，有望将用其来建立重叠下颌骨三维影像的共坐标系。

3.3 本研究提出的新的上颌骨重叠方法 鉴于本研究显示出8点优化可精准建立ELSA共坐标系，并考虑到颅面部各解剖结构间的位置关系存在的内在规律，如在8点优化后的ELSA共坐标系下，如二维头影重叠仅使用一条参考线即可重叠颅面部的三维的解剖结构，本研究也对该法进行了初步的探索。本研究结果显示即使经过8点优化法后，点ANS的重叠误差[(0.97±0.44)mm]依然大于点PNS[(0.83±0.38)mm]。且ANS共坐标系下x轴和z轴的重叠误差更大，且差异有统计学意义(P<0.05，图1D)。3种共坐标系间的平均线距重叠误差差异无统计学意义，但PNS共坐标系的平均角度重叠误差较ANS共坐标系更小且差异有统计学意义(P<0.05)。PNS共坐标系略优于ANS共坐标系。但PNS共坐标系和ANS共坐标系均仅使用2个点建立，因此重叠的平均角度误差应被重点考虑。笔者推荐在经8点优化法优化后的ELSA共坐标系下重叠上颌骨三维影像时，使用以PNS为原点的PNS共坐标系。

总之，本研究所提出的上颌骨三维影像的重叠方法，除标志点定点外，其余步骤均不需进行影像重建，也无需对某一解剖结构进行精确的人工分割，与传统的二维头影重叠方法相似，但可在三维方向分析上颌牙列相对于上颌骨的位置变化，很大程度降低了对硬件的要求，并因此提高了批量重叠影像的效率。

[1] Patel S, Horner K. The use of cone beam computed tomography in endodontics. Int Endod J, 2009,42(9):755-756.

[2] Grauer D, Cevidanes LH, Proffit WR. Working with DICOM craniofacial images. Am J Orthod Dentofac Orthop, 2009,136(3):460-470.

[3] DeCesare A, Secanell M, Lagravère MO, et al. Multiobjective optimization framework for landmark measurement error correction in three-dimensional cephalometric tomography. Dentomaxillofac Radiol, 2013,42(7):20130035.

[4] Lagravère MO, Major PW, Carey J. Sensitivity analysis for plane orientation in three-dimensional cephalometric analysis based on superimposition of serial cone beam computed tomography images. Dentomaxillofac Radiol, 2010,39(7):400-408.

[5] Lemieux G, Carey JP, Flores-Mir C, et al. Three-dimensional cephalometric superimposition of the nasomaxillary complex. Am J Orthod Dentofac Orthop, 2014,146(6):758-764.[6] Lagravère MO, Hansen L, Harzer W, et al. Plane orientation for standardization in 3-dimensional cephalometric analysis with computerized tomography imaging. Am J Orthod Dentofac Orthop, 2006,129(5):601-604.

[7] Lagravère MO, Secanell M, Major PW, et al. Optimization analysis for plane orientation in 3-dimensional cephalometric analysis of serial cone-beam computerized tomography images. Oral Surg Oral Med Oral Pathol Oral Radiol Endod, 2011,111(6):771-777.

[8] Cevidanes LH, Bailey LJ, Tucker GR Jr, et al. Superimposition of 3D cone-beam CT models of orthognathic surgery patients. Dentomaxillofac Radiol, 2005,34(6):369-375.

[9] Cevidanes LH, Styner MA, Proffit WR. Image analysis and superimposition of 3-dimensional cone-beam computed tomography models. Am J Orthod Dentofac Orthop, 2006,129(5):611-618.

[10] da Motta AT, de Assis Ribeiro Carvalho F, Oliveira AE, et al. Superimposition of 3D cone-beam CT models in orthognathic surgery. Dental Press J Orthod, 2010,15(2):39-41.

[11] Nada RM, Maal TJ, Breuning KH, et al. Accuracy and reproducibility of voxel based superimposition of cone beam computed tomography models on the anterior cranial base and the zygomatic arches. PLoS One, 2011,6(2):e16520.

[12] Lee JY, Kim YI, Hwang DS, et al. Effect of setback Le Fort I osteotomy on midfacial soft-tissue changes as evaluated by cone-beam computed tomography superimposition for cases of skeletal Class Ⅲ malocclusion. Int J Oral Maxillofac Surg, 2013,42(6):790-795.

[13] Lemieux G, Carey JP, Flores-Mir C, et al. Precision and accuracy of suggested maxillary and mandibular landmarks with cone-beam computed tomography for regional superimpositions: An in vitro study. Am J Orthod Dentofacial Orthop, 2016,149(1):67-75.

[14] Lagravère MO, Low C, Flores-Mir C, et al. Intraexaminer and interexaminer reliabilities of landmark identification on digitized lateral cephalograms and formatted 3-dimensional cone-beam computerized tomography images. Am J Orthod Dentofacial Orthop, 2010,137(5):598-604.

[15] Uzel A, Özyürek Y, Öztunç H. Condyle position in Class Ⅱ Division 1 malocclusion patients: Correlation between MPI records and CBCT images. J World Fed Orthod. 2013:2(2):e65-e70.

Optimization for landmarks-based three-dimensional cephalometric superimposition and a method for superimposition of three-dimensional image of maxilla

WENGYao,WANGZiyi,ZHANGXiaodong*

(DepartmentofStomatology,theGeneralHospitalofShenyangMilitaryRegion,Shenyang110840,China)

Objective To optimize the existed landmarks-based-superimposition technique, and to propose a new simple method for regional superimposition of the maxillary complex. Methods Totally 9 volunteers were included, who were performed twice cone beam CT (CBCT) in one-year interval. ELSA co-ordinate were corrected using two kind of numerical optimization algorithm (6-point method and 8-point method), and the operator error of landmark location were compared. The anterior and posterior nasal spine (ANS and PNS) co-ordinate system were constructed only using two anatomical landmarks (ANS and PNS) for regional superimposition of the maxillary complex. Several landmarks were pick up to evaluate the error of superimposition and analyze the difference by statistic method. Results In correction, 6-point method and 8-point method, the average error of linear and angle measurement of the ELSA co-ordinate were (0.60±0.47)mm and (0.49±0.38)°, (0.44±0.39)mm and (0.48±0.37)°, (0.41±0.34)mm and (0.41±0.32)° respectively. The average error of linear measurements significantly decreased (P<0.05) in 8-point method. The average error of superimposition of all picked landmarks on ELSA co-ordinate were (0.95±0.50)mm and (1.06±0.65)°, (0.92±0.54)mm and (0.92±0.58)°, (0.80±0.43)mm and (0.87±0.59)° respectively. The differences had statistical significance (P<0.000 1). In optimized by 8-point method, the average error of superimposition of all picked landmarks on ELSA, ANS and PNS co-ordinate were (0.92±0.47)mm and (1.14±0.66)°, (0.99±0.47)mm and (1.33±0.64)°, (1.00±0.62)mm and (1.08±0.70)° respectively. Conclusion Significant improvement of superimposition is observed using 8-point method. The improved method is accuracy to analyze the clinical data.

Cone-beam computed tomography; Three-dimensional superimposition; Optimization; Algorithm; Cephalometrics

辽宁省自然科学基金(2015020428)。

翁瑶(1989—)，女，辽宁沈阳人，硕士，医师。研究方向：口腔正畸。E-mail: hsbr@icloud.com

张晓东，沈阳军区总医院口腔内科，110840。E-mail: zxd99233@163.com

2016-06-18

2016-10-17

R814.42

A

1003-3289(2017)01-0124-08

10.13929/j.1003-3289.201606089