中考计算概率常用五法

华昭琴

(江苏省姜堰区实验初级中学 225500)

概率计算是中考命题的热点内容，常用的计算方法有以下五种：

一、完全枚举法

例1 (2015年山东德州)经过某十字路口的汽车，可能直行，也可能左转或者右转.如果这三种可能性大小相同，则经过这个十字路口的两辆汽车一辆左转，一辆右转的概率是( ).

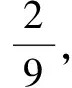
说明：此题考查了枚举法求概率的方法，先枚举出事件的所有可能情况和满足要求的情况，再应用“概率=所求情况数与总情况数之比”求解．

二、列表法

例2 (2015年湖北恩施)质地均匀的小正方体，六个面分别有数字“1”、“2”、“3”、“4”、“5”、“6”，同时投掷两枚，观察朝上一面的数字．

(1)求数字“1”出现的概率；

(2)求两个数字之和为偶数的概率．

分析(1)列表得出所有等可能的情况数，找出数字“1”出现的情况数，即可求出所求的概率；(2)找出数字之和为偶数的情况数，即可求出所求的概率．

解(1)列表如下：

1234561(1，1)(2，1)(3，1)(4，1)(5，1)(6，1)2(1，2)(2，2)(3，2)(4，2)(5，2)(6，2)3(1，3)(2，3)(3，3)(4，3)(5，3)(6，3)4(1，4)(2，4)(3，4)(4，4)(5，4)(6，4)5(1，5)(2，5)(3，5)(4，5)(5，5)(6，5)6(1，6)(2，6)(3，6)(4，6)(5，6)(6，6)

说明：列表法适合于两步完成的事件，注意：概率=所求情况数与总情况数之比．

三、树状图法

例3 (2015年安徽)A、B、C三人玩篮球传球游戏，游戏规则是：第一次传球由A将球随机地传给B、C两人中的某一人，以后的每一次传球都是由上次的传球者随机地传给其他两人中的某一人．

1.求两次传球后，球恰在B手中的概率；

2.求三次传球后，球恰在A手中的概率．

分析(1)首先根据题意画出树状图，然后由树状图求得所有等可能的结果与两次传球后，球恰在B手中的情况，再利用概率公式即可求得答案；(2)首先根据题意画出树状图，然后由树状图求得所有等可能的结果与三次传球后，球恰在A手中的情况，再利用概率公式即可求得答案．

解(1)画树状图得：

说明：本题考查的是用画树状图法求概率，画树状图法可以不重复不遗漏的列出所有可能的结果，它适合两步或两步以上完成的事件．

四、面积计算法

例4 (2015年内蒙古呼和浩特)如图，四边形ABCD是菱形，E、F、G、H分别是各边的中点，随机地向菱形ABCD内掷一粒米，则米粒落到阴影区域内的概率是 ．

说明：当某一事件A发生的可能性大小与相关图形的面积大小有关时， 概率的计算方法是事件A所有可能结果所组成的图形的面积与所有可能结果组成的总图形面积之比，即

五、实验法

例5 (2015年江苏扬州)色盲是伴X染色体隐性先天遗传病，患者中男性远多于女性，从男性体检信息库中随机抽取体检表，统计结果如下表：

抽取的体检表数n501002004005008001000120015002000色盲患者的频数m37132937556985105138色盲患者的频率m/n0．0600．0700．0650．0730．0740．0690．0690．0710．0700．069

根据上表，估计在男性中，男性患色盲的概率为 (结果精确到0.01).

解析通过多次重复的实验，将随机事件的频率的稳定值作为随机事件发生的概率．由表格可以发现，随着抽取的体检表数字的增加，男性色盲患者的频数在增加，男性色盲患者的频率逐步稳定在0.070左右，因此估计在男性中，男性患色盲的概率为0.70.

说明：此题考查了利用频率估计概率，大量反复试验下频率稳定值即概率．用到的知识点为：频率=所求情况数与总情况数之比．

[1]陈德前. 中考中概率计算的常用方法[J].中学生数理化(中考版)，2014(7-8).