一道中考题的阅卷分析与反思

胡小明

(江苏省连云港外国语学校 222000)

在2017的中考阅卷中，本人负责连云港中考试卷的第25题，如下：

25.(本题满分10分)如图，湿地景区岸边有三个观景台A、B、C.已知AB=1400米，AC=1000米，B点位于A点的南偏西60.7°方向，C点位于A点的南偏东66.1°方向.

1.求△ABC的面积；

2.景区规划在线段BC的中点D处修建一个湖心亭，并修建观景栈道AD.试求A、D间的距离.(结果精确到0.1米)(参考数据：

sin53.2°≈0.80,cos53.2°≈0.60,

sin60.7°≈0.87,cos60.7°≈0.49,

该题是一道三角函数的应用问题，出得较为巧妙，对学生基本知识和基本技能的考查很到位.同时作为试卷的倒数第4题，按理说应该难度不是很大，但阅卷发现，本题分值为10分，但全市得分率只有约1.7分，低于我们的预料，背后原因值得我们反思.在阅卷中我们也发现了除参考答案外的多种巧妙方法，也发现了学生的不少误区，下面简单谈谈.

一、典型正确做法

关于本题的做法，多种多样，但我们发现学生主要有以下几种方法非常巧妙，值得推荐.

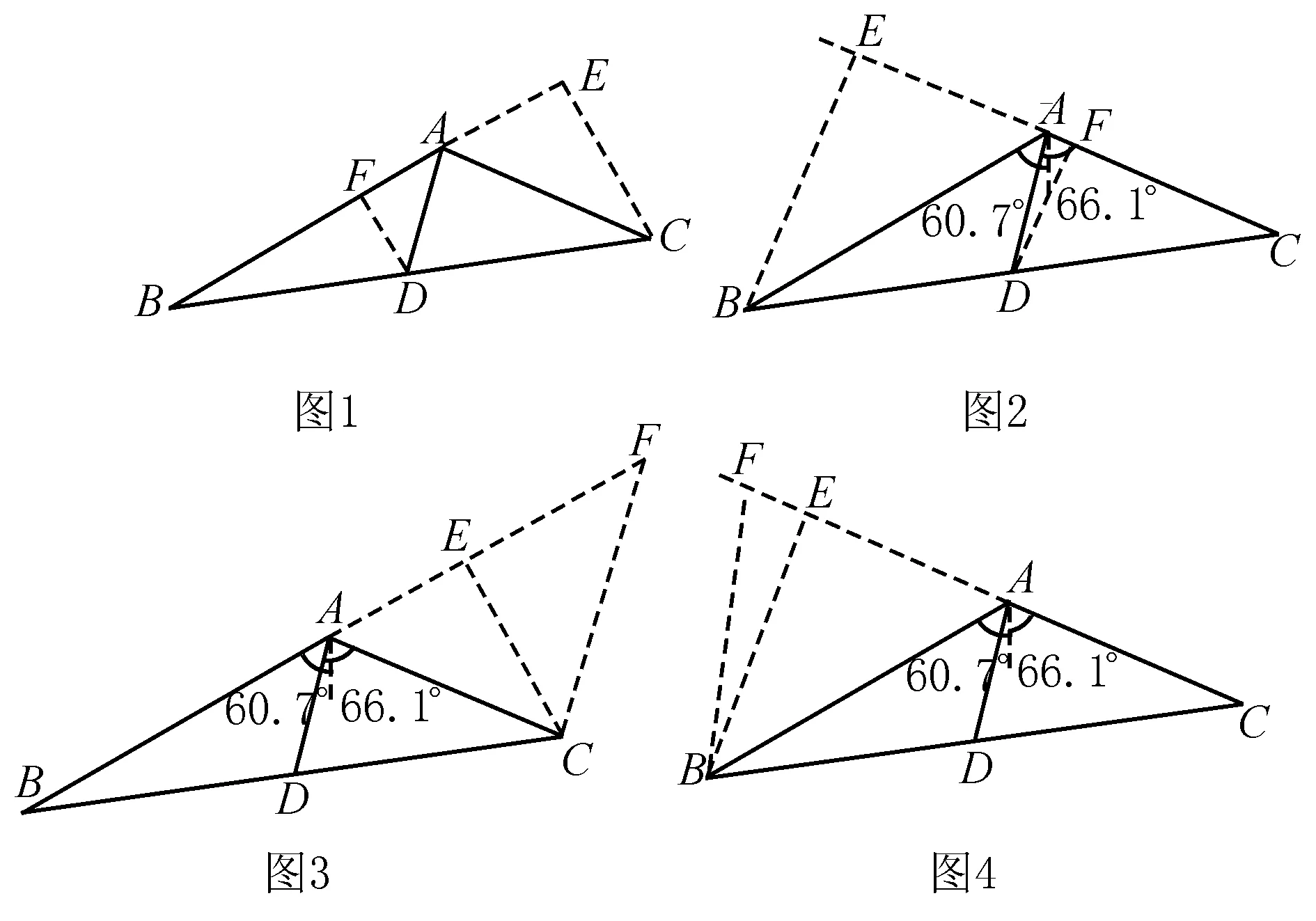
图1就是参考答案提供的方法：先作出AB边上的高CE，再作DF⊥AB，从而构建出中位线DF，再在直角三角形ADF中利用勾股定理求出AD.

图2 的方法和图1的方法实质上一样的，就是先作出AC边上的高BE，再作DF⊥AC，从而构建出中位线DF，再在直角三角形ADF中利用勾股定理求出AD.

图3 是一种巧妙的方法：先作出AB边上的高CE，再在AE的延长取点F，使AF=AB,从而构建出中位线AD，再在直角三角形ECF中利用勾股定理求出CF,从而求出AD.

图4的方法和图3的方法实质上一样的，先作出AC边上的高BE，再在CA的延长取点F，使AF=AC,从而构建出中位线AD，再在直角三角形EBF中利用勾股定理求出BF,从而求出AD.

综合看这几种方法，两问都是一气呵成，实质上都是作高，再构建中位线！

也有学生用较为复杂的方法，

图5和图6，都是“割补法”中的“补”的方法，分别补成矩形和直角梯形来做的，但只能解决第一问.

二、典型错误做法和误区

1.基本概念不清.不理解方向角(甚至有人认为南北方向与BC垂直)，不能正确作出对应的高，或三角函数的概念不清，从而求高出错.

2.运算能力较弱.本题的数据较大，在计算的过程或结果中多“0”或少“0”，已经成为经常现象.

3.解题思路不清.第一问较简单，不少同学舍易求繁，甚至做不出来.第二问不会分析条件，D为中点这个条件，不能联想到中位线，从而找不到解题思路.

4.说理不够严谨.有些该写出来的说理过程被省略了，想当然的就直接运用了，导致丢了过程分.

三、以后教学建议

1.加强基础知识和基本技能教学.如，要让学生学会正确作出钝角三角形三边上的高.

2.不能忽视对三角函数的教学.三角函数是九下的内容，不能为了提前总复习而压缩上新课的时间，也不能过度强调特殊角的三角函数，一般角其实也是一样.

3.教会学生必要的解题技巧.如，“见中点，想中位线”；“遇直角三角形，想勾股定理”等等.

[1]罗增儒. 中学数学解题的理论与实践[M].南宁：广西教育出版社，2008.

[2]裴光亚. 数学教师的专业发展:在书房与教室间穿行的教研人生[M].西安：陕西师范大学出版总社，2013.