传承 创新 发展——2016年安徽中考压轴题赏析

冯章成

(安徽省合肥市第四十二中学中铁国际城校区 230031)

每年安徽中考数学压轴题，倍受中考命题者、试题研究者以及广大初中毕业班师生的青睐.2016年的数学压轴题更是如此，学生拿到题目有种似曾相识的感觉，的确如此.2016年的数学压轴题继续采用经典的基本模型作为背景，但又不拘泥于基本模型，在传承基本模型的基础上，精心研究，加以创新，拓展提高，发展学生的能力.一题多问的设计具有很好的层次性、启发性、关联性和发展性.下面就该题采用的模型以及该题的设计和具体解法赏析如下.

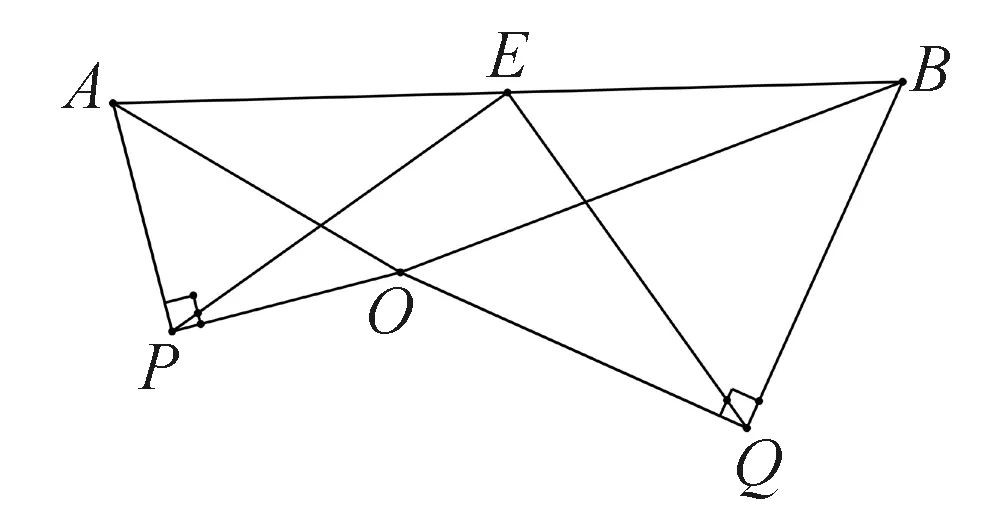
经典模型呈现: 已知，如图，PA=PO，QB=QO，∠APO=∠BQO=90°,点E为AB中点；求证：PE=QE，PE⊥QE.

分析这是两等腰直角三角形共一锐角顶点的经典模型，此模型的经典之处就在于：两斜边的夹角不论如何变化，上述结论恒成立.下面先来证明这两结论.

证明分别取OA、OB的中点C和D，连接CP、CE、DQ、DE.

∵点C、D、E分别是OA、OB、AB的中点,

∴DE和CE是△AOB的中位线,

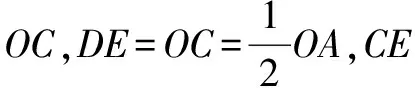
∴四边形ODEC是平行四边形,

∴∠OCE=∠ODE.

∵PA=PO，QB=QO，∠APO=∠BQO=90°,

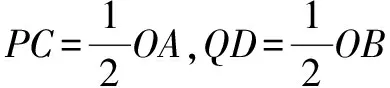
PC⊥OA，QD⊥OB,

∠PCO=∠QDO=90°.

∴PC=ED，CE=DQ，∠PCE=∠EDQ,

∴△PCE≌△EDQ,

∴PE=QE，∠CPE=∠DEQ.

∵DE∥OC,

∴∠OCE+∠CED=180°.

又∵∠PCE+∠CPE+∠CEP=180°,

∴∠OCE+∠CED=∠PCE+∠CPE+∠CEP,

即∠OCE+∠CEP+∠DEQ+∠PEQ=∠OCE+∠PCO+∠CEP+∠CPE,

∴∠PEQ=∠PCO=90°,

∴PE⊥QE.

2016年安徽中考压轴题原题呈现:

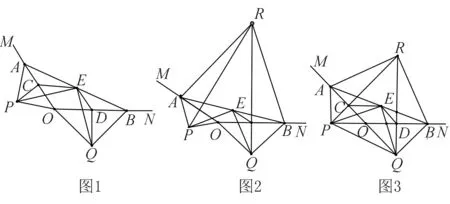
如图1，A,B分别在射线OM，ON上，且∠MON为钝角.现以线段OA,OB为斜边向∠MON的外侧作等腰直角三角形，分别是△OAP, △OBQ,点C,D,E分别是OA,OB,AB的中点.

(1)求证: △PCE≌△EDQ；

(2)延长PC,QD交于点R,

①如图2，若∠MON=150°，求证：△ABR为等边三角形；

参考答案及评分标准呈现：

(1)证明: ∵点C,D,E分别是OA,OB,AB的中点,

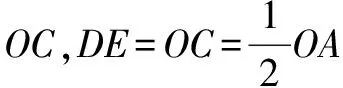
∴四边形ODEC是平行四边形,

∴∠OCE=∠ODE.

又∵△OAP, △OBQ都是等腰直角三角形,

∴∠PCO=∠QDO=90°,

∴∠PCE=∠PCO+∠OCE=∠QDO+∠ODE=∠EDQ.

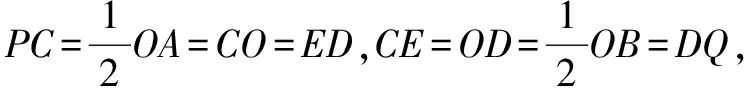
∴△PCE≌△EDQ.(5分)

(2)①证明：如图1，连接OR.

∵PR与QR分别为线段OA与OB的中垂线,

∴AR=OR=BR, ∠ARC=∠ORC, ∠ORD=∠BRD.

在四边形OCRD中，∠OCR=∠ODR=90°, ∠MON=150°,∴∠CRD=30°.

∴∠ARB=∠ARO+∠BRO=2∠CRO+2∠ORD=2∠CRD=60°,

∴△ABR为等边三角形.(9分)

②解:如图2，由(1)知EQ=PE, ∠DEQ=∠CPE.

∴∠PEQ=∠CED-∠CEP-∠DEQ=∠ACE-∠CEP-∠CPE=∠ACE-∠RCE=∠ACR=90°,

即△PEQ为等腰直角三角形.

由于△ARB∽△PEQ，所以∠ARB=90°.

于是在在四边形OCRD中，∠OCR=∠ODR=90°,

∴∠MON=135°.

此时P、O、B在一条直线上，△PAB为直角三角形且∠APB为直角.

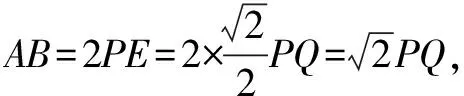
三个问题的设计层层递进，相互关联，具有一定的启发性和发展性.第一问直接把模型的证明方法展示出来了，不扭扭捏捏遮遮掩掩.可以说是起点低、易上手.符合学生的认知特点，使得不同认知水平、不同学习经历的学生都能迅速积极参与到问题的探究和解决中来.

[1]安徽省教育考试院. 2016年初中毕业学业考试试题、参考答案及评分标准[Z]，2016：6-10.