学会多角度寻找解题思路

李月恬 陈德前

(江苏省姜堰区实验初级中学 225500;江苏省兴化市教育局教研室 225700)

本文以一些典型的中考题为例，来谈谈如何多角度地寻找解题思路.

例1 若2a-b=5，则多项式6a-3b的值是____．

解法1 (参数代入法)将a当做已知数(参数)，根据“减数等于被减数减去差”，可得b=2a-5，则6a-3b=6a-3(2a-5)=6a-6a+15=15.

解法2 (整体代入法)把6a-3b变形为3(2a-b)，然后把2a-b整体代入，即可求得其值.6a-3b=3(2a-b))=3×5=15.

解法3 (特值代入法)取a=0，则b=-5，当a=0，b=-5时，6a-3b=0-3×(-5)=15.

反思回味：对于给定的条件，要善于从多角度来看，这里解法1 是将字母a看作常数来参与运算的；方法2是从整体的角度来看的，从待求的代数式中变换出已知条件式2a-b，整体代入，十分简捷，也可以将已知式两边同时乘以3，整体得出结论；方法3是从特殊与一般的角度来看的，巧妙地取a=0，则b为整数-5，代入求值式计算比较简捷，在用这种方法解题时要注意两点：一是所取的字母值要使已知式和求值式有意义，二是所取的字母值要使计算简便.

例2 化简：x-{-5x-〔-y+(-x+3y)+x〕}.

分析本题中含有多层括号，可以先去小括号，再去中括号，最后去大括号； 也可以先去大括号，再去中括号，最后去小括号；联想到学习相反数时化简多重括号的方法，还可以得到一种更简捷的方法：要确定每一项最后结果的符号，就是数“-”号的个数，如果是奇数个，那么结果的符号为负；如果是偶数个，那么结果的符号为正，这样就可以一次性去掉所有括号．

解法1 原式=x-{-5x-〔-y-x+3y+x〕}=x-{-5x-〔+2y〕}=x-{-5x-2y}=x+5x+2y=6x+2y.

解法2 原式=x+5x+〔-y+(-x+3y)+x〕=6x-y+(-x+3y)+x=7x-y-x+3y=6x+2y.

解法3 原式=x+5x-y-x+3y+x=6x+2y．

反思回味：解法1是解决这类问题时最常用的方法，即从里到外去括号，要注意每去一次括号后就要将可合并的同类项合并起来，这样就减少了项数，既可以避免错误，又可以简化计算. 解法2与解法1的思路正好相反，从外向里去括号，运用了整体思想，去大括号时，将中括号看作一个整体，去中括号时将小括号看作一个整体.解法3给出了化简多重括号的一种简捷方法，即通过数“-”号的个数来判断每一项最后结果的符号：如果是奇数个，那么结果的符号为负；如果是偶数个，那么结果的符号为正.这个法则可简记为“奇负偶正” ．

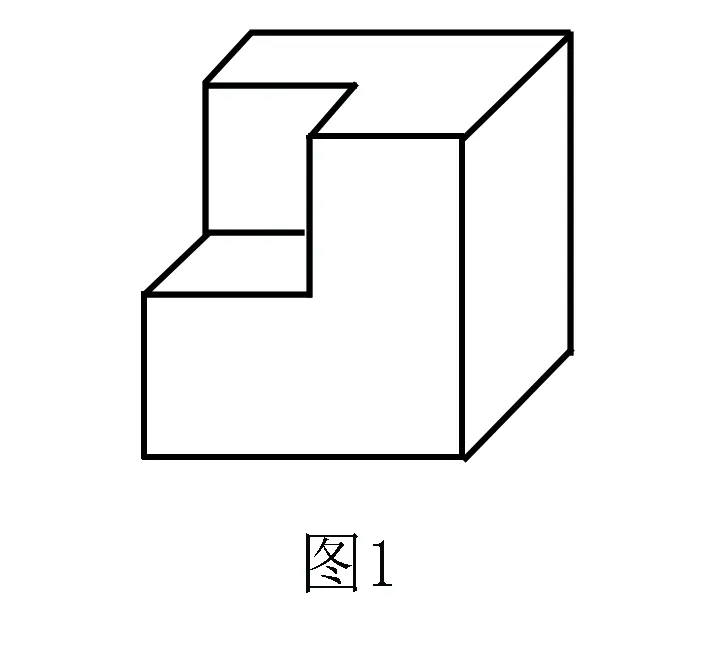
例3 从棱长为2的正方体毛坯的一角，挖去一个棱长为1的小正方体，得到一个如图1所示的零件，则这个零件的表面积为 ．

分析解决本题首先想到的是计算出各个“外露”部分表面的面积，再求和，容易产生遗漏或重复；仔细观察发现，从正方体毛坯中挖去一个棱长为1的小正方体，则这个零件的表面积通过补形就等于原正方体的表面积，计算就十分简单.

解法1 这个零件的表面积=2×2×3+1×1×3+(2×2-1×1)×3=24.

解法2 这个零件的表面积=2×2×6=24.

反思回味：这类题的最大特点是不需要怎样去计算，只靠仔细观察结合实际经验，就很容易解决，掌握视图的概念是解题的关键.这里采用的技巧就是补形，即将问题中的原图形(非规则图形或非特殊图形)经过添加辅助线以后，转化为一个完整的特殊图形，让问题中的隐含条件显露出来，从而使问题得以简捷获解．

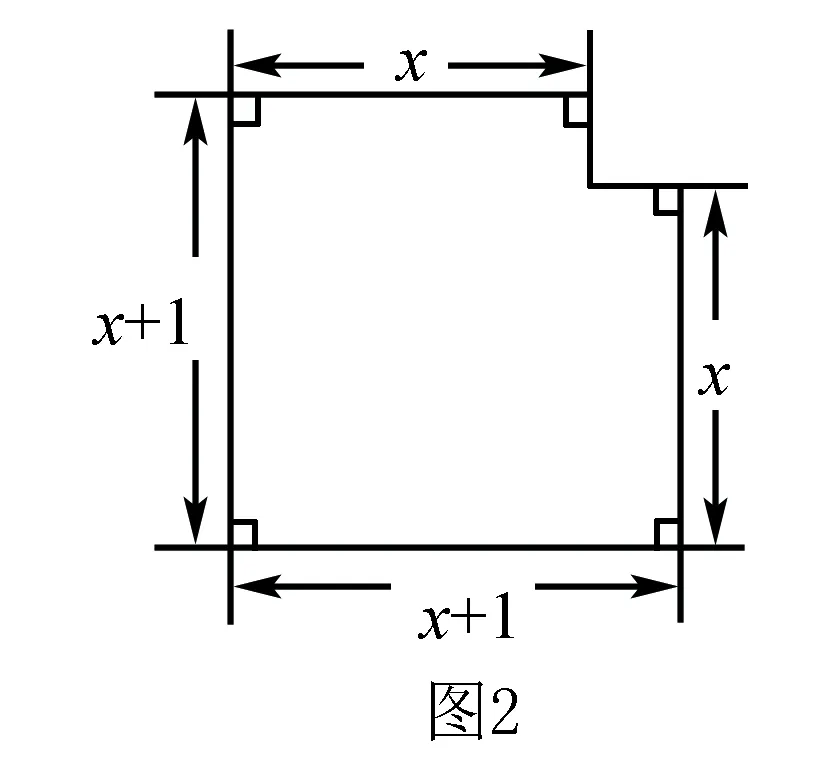
例4 已知如图2所示的图形的面积为24，根据图中的条件，可列出方程： ．

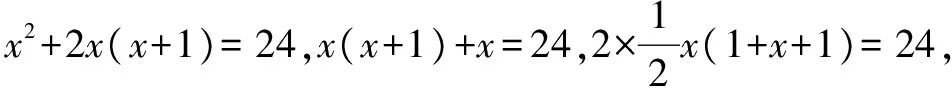
反思回味：本题尽管是一道“小题”，但它“小题大做”，能充分考查了不同层次解题者的思维水平和数学思想方法的应用能力．在每一种思路下得到的方程的简繁程度是一目了然的，但这些方程本质上是相同的，因此给出的众多答案可以把不同层次解题者的思维层次充分地映射出来，所以说，本题是题目小，功能大．

例5 灾后重建，四川从悲壮走向豪迈．灾民发扬伟大的抗震救灾精神，桂花村派男女村民共15人到山外采购建房所需的水泥，已知男村民一人挑两包，女村民两人抬一包，共购回15包．请问这次采购派男女村民各多少人？( ).

A．男村民3人，女村民12人

B．男村民5人，女村民10人

C．男村民6人，女村民9人

D．男村民7人，女村民8人

分析这是一道典型的实际问题应用题，随着我们思考角度的不同，解法也不一样：

视角1(设直接未知数列一元一次方程求解的角度)：题目中有两个等量关系：一是男村民人数+女村民人数=15人，二是男村民挑的水泥包数+女村民挑的水泥包数=15包．现在要求的是这次采购派男女村民各多少人，有两个未知数，根据第一个等量关系知，可设直接未知数，设其中一个未知量为x人，则由第一个等量关系可知另一个未知量为(15-x)人，再由第二个等量关系列方程求解．

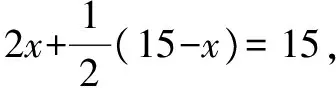
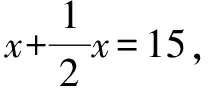
视角2(设间接未知数列一元一次方程求解的角度)：题目中有两个等量关系：一是男村民人数+女村民人数=15人，二是男村民挑的水泥包数+女村民挑的水泥包数=15包．现在要求的是这次采购派男女村民各多少人，这可以通过求出男、女村民挑的水泥包数来求出．根据第二个等量关系，可设间接未知数，设其中一个未知量为x包，则由第二个等量关系可知另一个未知量为(15-x)包，再由第一个等量关系列方程求解．

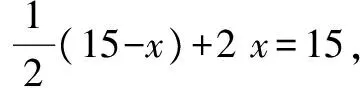
视角3 (从分组的角度)：因为男村民一人挑两包，女村民两人抬一包，所以可以把一个男村民和两个女村民分成一组，每组3人挑3包水泥，15个人可以分为5组，5组15人挑15包水泥，这样这次采购派男女村民人数就一目了然了．

解法3 一个男村民和两个女村民分成一组，则每组3人挑3包水泥，则5组村民15人正好挑15包水泥，5组中有5个男村民和10个女村民，选B．

反思回味：解决实际问题应用题，方程是最有效的模型之一，随着未知数选择的不同，得到的解法也不一样；数量关系选择的不同，得到的解法也不一样；由于题目没有要求用方程来求解，所以采用算术方法来解决本题更简捷.

[1]杭永根，陈德前.开放探究问题(3)[J].中学数学教学参考(中旬)，2017(1-2)：105-109.

[2]霍彩霞.如何进行审题[J].初中生学习指导(七年级)，2016(7-8)：98-101.