数学解题课堂因学生的动态生成而精彩

郑苗华

(浙江省台州市黄岩区新前中学 318020)

在教学“操作类问题”的中考专题复习课时，笔者选用了一道题作为本节课的例题：

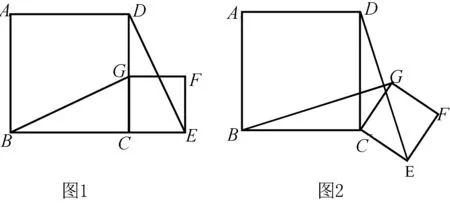
如图①，已知正方形ABCD与正方形CEFG的边长分别为a,b(a>b),连接DE,BG.

(1)求证：DE=BG；

(2)固定正方形ABCD，将正方形CEFG绕顶点C顺时针旋转角度α(0°<α<360°)如图②，试判断DE与BG还相等吗？它们的位置关系如何？说明你的理由.

基于上题全等与旋转意识的唤醒，“续挖枯井有甘泉”，从而进行以下的两题的改编：

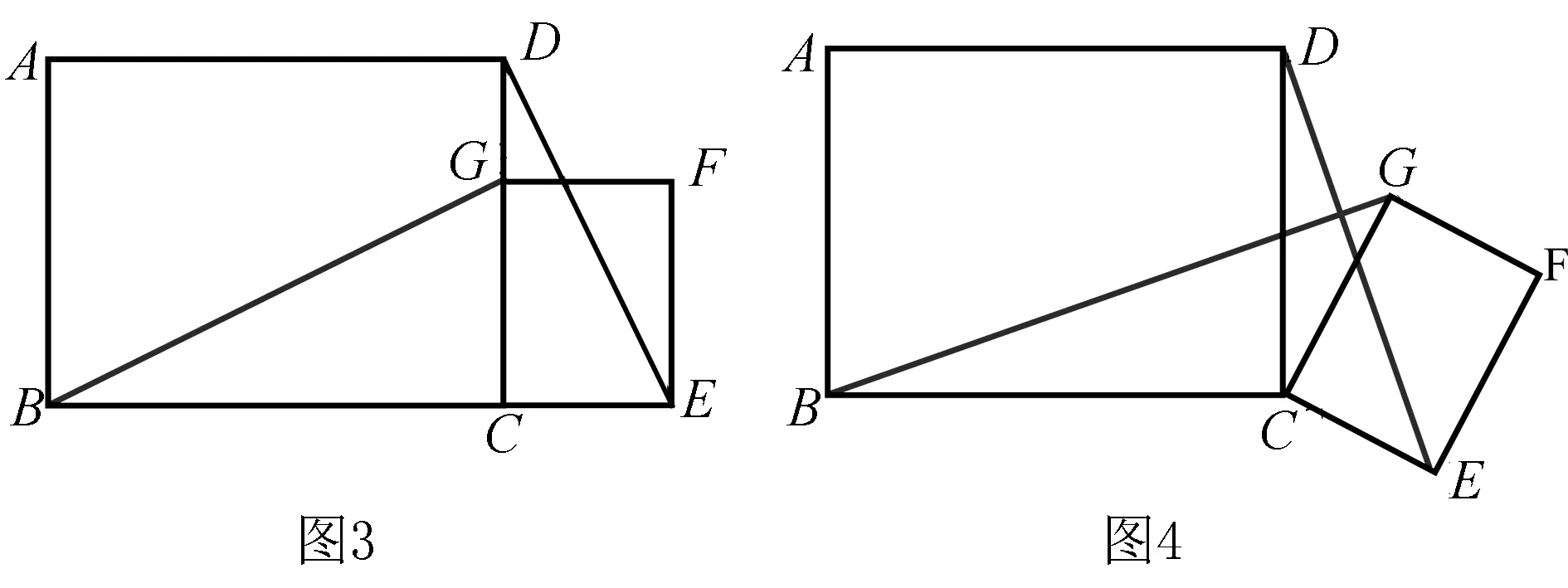
改编题1：如图③：矩形ABCD与矩形CEFG相似，边长分别为a,b(a>b),连接DE,BG.

(1)试判断DE与BG的位置关系，说明你的理由；

(2)如图④，固定矩形ABCD，矩形CEFG绕顶点C顺时针旋转角度α(0°<α<360°)，试判断DE与BG的位置关系,说明你的理由.

改编题2：探究: 已知正方形ABCD与正方形CEFG的边长分别为a,b(a>b),连接DE,AF. 固定正方形ABCD，将正方形CEFG绕顶点C顺时针旋转角度α(0°<α<180°)如图，在图形的旋转变换中,我们发现DE,AF的长度也随旋转而发生着变化.为探究AF与DE之间的函数关系，设DE=x,AF=y.

(1)若a=4cm，b=2cm,则在旋转过程中，函数值y的取值范围为____;

(2)试探究y与x之间的函数关系式.

改编1题目结构、求解思路与原题基本一致，学生能类比解答，所以重点围绕改编2的两小题展开小组合作讨论.笔者让学生自主审题环节中，充分留足了学生思考的时间，“静待花开”.在接下来的课堂教学中，围绕两小题呈现了学生“疑点争论”的场景.

关于第(1)小题，“疑点争论”如下：

学生2：不对！

教师：同学们，你们现在认可哪种观点啊？

包括学生1、学生2在内的全体学生都表示同意学生3的观点.

教师：通过本小题的解答，你们从中能得到哪些启示呢？

学生4：我认为操作类问题应认真分析操作的所有步骤，画出各种不同情形的图形进行分析比较，不能只考虑局部.

学生5：我认为涉及取值范围的题目应特别留心等号能否取得.

教师：说得都很好.现在考考你们：若将条件“0°<α<180°”改为“0°<α≤360°”，第(1)小题的结果又如何？

学生7：由改编1启发，构建AF，DE所在一对相似三角形后，就能得到相应函数关系式了.在这种想法下，我通过尝试找到了方法，分别连接AC，CF，易证△ACF∽△DCE，得…

随后，课堂上又出现了“疑点争论”：

学生8：你的解题方法是正确的，不过这样解答是不够完整的，你只考虑了旋转角度α为锐角的情形，还需考虑α为钝角的情形.

学生9：不需要的.在刚才大家讨论第(1)小题的时候，我就想到了第(2)小题也要分类讨论，不过，解答是一样的.

学生8：不是的.粗看解答一样，但是还是需要分类讨论的，画出α为钝角的相应图形之后，就可发现推理中关于那对三角形的对应角在证明其相等时是有区别的，不信你试试看.

学生9(想一想)：确实如此，谢谢提醒，我明白了.

教师：其他同学还有补充吗？

学生10：是不是还要考虑α为直角的情形啊？

学生11：是的.

学生12：你多虑了，这道题是不用考虑α为直角的情形的，因为α=90°时，刚才所说的那对相似三角形根本就不存在.

教师：你们刚才的对话很精彩，现在问题的焦点集中到要不要考虑α=90°的情形.

学生13：我觉得尽管此时△ACF与△DCE并不存在，但还是要考虑这种情形的，因为α=90°也是在0°<α<180°范围内，若不考虑就遗漏了一种情形.可是我不知道具体怎么求.

美国教育家布鲁巴克认为：“最精湛的教学艺术，遵循的最高准则，就是学生自己提出问题.”让学生主动参与且提出疑问就是我们教师的教学核心，这就是课堂的动态生成，是学生思维学习的长效利益，教师应和学生一起疑点追踪，探究闪光智慧,不能“好心帮助”.因此，教师应该鼓励学生敢于质疑、乐于提问，并引导学生学会对话与交流，让课堂上回荡着质疑的声音，促进学生思维能力的提高.

[1]庞彦福.初中数学有效教学[M].北京：北京师范大学出版集团,2015.

[2]雷玲.中学数学名师教学艺术[M].上海：华东师范大学出版社,2014.