基于区间直觉模糊集的目标优先级求解方法*
徐公国,段修生,李胜军
(军械工程学院,石家庄050003)
基于区间直觉模糊集的目标优先级求解方法*
徐公国,段修生,李胜军
(军械工程学院,石家庄050003)
针对复杂防空作战环境下多目标优先级难以准确评估的问题,提出了基于区间直觉模糊集理论的目标优先级求解算法。首先系统分析了影响目标优先级的因素以及各影响因素与目标优先级之间的非线性关系。其次,对区间直觉模糊集的得分函数和精确函数进行了改进,考虑了犹豫度信息对决策结果的影响,并且提出了基于得分函数和精确函数的目标优先级求解算法。最后通过仿真算例验证了算法的有效性。
目标优先级,威胁度,区间直觉模糊集,得分函数,精确函数
0 引言
在地面防空武器系统中,特别是防空C3I系统中,目标优先级评估是武器-目标配对问题中的关键技术。目标优先级排序是涉及多领域、多层次的不确定性知识推理问题。目前主要有层次分析法、规划识别、贝叶斯推理[1]、神经网络法[2]等,每种方法各有所长,有不同的适用情形,但对于处理复杂战场环境下多目标模糊信息的情形均表现不佳。
保加利亚学者Atanassov[3]在1986年对模糊集进行了拓展,把仅考虑隶属度的模糊集推广到同时考虑隶属度、非隶属度和犹豫度3个方面信息的直觉模糊集,它在处理多变性和不确定性等实际问题中更具有灵活性和实用性。近年来,人们开始把区间直觉模糊理论运用到多属性决策问题中来,并且取得了较好的研究成果[4]。
针对复杂战场环境下目标属性测度的不确定性和短时多变性,将区间直觉模糊集理论运用到目标的威胁度评估和目标优先级排序问题中来,将使得求解算法有很强的泛化能力,在处理战场模糊信息时更具实用性。系统分析了目标威胁度评估的影响因素,对区间直觉模糊集的得分函数与精确函数进行了改进,并由此提出了基于区间直觉模糊集理论的目标优先级求解算法,最后通过仿真实验验证了算法的有效性。
1 区间直觉模糊集基本理论
1.1 区间直觉模糊集
定义1:设X为一非空论域,一个X上的直觉模糊集A定义为:

其中μA(x)和υA(x)为直觉模糊集A的隶属度函数和非隶属度函数,其中μA(x)∈[0,1],υA(x)∈[0,1],且有0≤μA(x)+υA(x)≤1。则进一步定义πA(x)=1-μA(x)-υA(x)为直觉模糊集A的犹豫度函数,其中πA(x)∈[0,1]。
由于客观事物的复杂性,隶属度与非隶属度的值往往难以用精确的实数值来表达,而用区间数形式表达则比较适合,故Atanassov又对直觉模糊集进行了扩展,提出了区间直觉模糊[5]概念,即μA(x)和υA(x)用区间的形式表示:μA(x)=[μAL(x),μAU(x)],υA(x)=[υAL(x),υAU(x)],且0≤μAL(x),0≤υAL(x),0≤μAU(x)+υAU(x)≤1。同时区间直觉模糊集A的犹豫度函数用区间表示为:

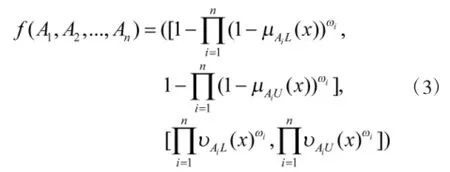
其中,ωi∈[0,1]为Ai,i=1,2,…,n的权重,ω1+ω2+…+ωn=1。
1.2 区间直觉模糊集的得分函数与精确函数
定义2[6]:选取一组区间直觉模糊数为:,其中i=1,2,…,n。定义区间直觉模糊集得分函数和精确函数为S(Ai)和H(Ai):
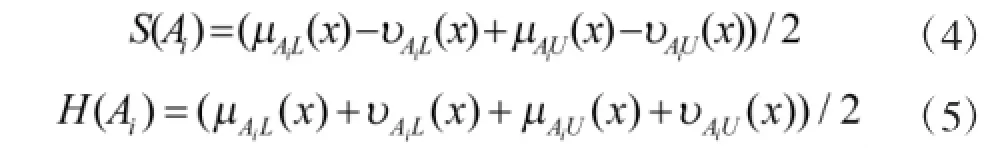
得分函数和精确函数类似于统计学中的均值与方差。得分函数越大,区间直觉模糊数对应的方案越优,在得分函数相等的情况下精确函数越大则对应的方案越优。但是上述函数没有考虑犹豫度对决策结果的影响,有其局限性。例如:取两组区间直觉模糊数为A1=([0.4,0.5],[0.3,0.4]),A2=([0.4,0.5],[0.2,0.5]),则有S(A1)=S(A2)=0.1,H(A1)=H(A2)= 0.8,由于得分函数和精确函数的值都相等,并没有区分出A1和A2的优劣,可见上述函数有其不足之处。为此对得分函数和精确函数进行改进,改进后的函数如式(6)和式(7)所示。
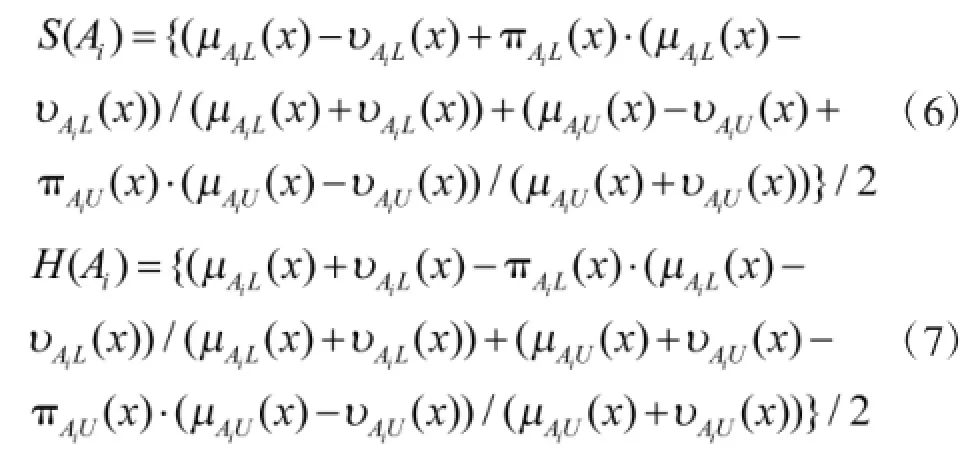
改进后的得分函和精确函数在计算时考虑了犹豫度信息对决策结果的影响,使得决策结果更准确。此时再对算例进行分析,按式(6)计算出A1和A2的得分函数,得S(A1)=0.127 0,S(A2)=0.166 7。由此可见所对应的方案较优,也与其非隶属度较小的实际情况相符,可见改进计算方法的合理性。
2 目标优先级影响因素及其权重求解
2.1 目标优先级影响因素的选取
影响目标优先级的因素有很多,针对不同的作战任务的侧重点也会不一样,可以确定的是目标威胁度越大,目标的优先级越高。针对地面防空武器系统的特点,目标威胁度主要根据目标类型、是否有攻击意图、攻击地面何种目标、目标的速度、航向以及目标突防的概率等因素[1-2,7]综合确定的。这些因素一般是模糊的、多变的,故需设置相应量化标准。
目标身份:目标身份主要分为敌、我、不明,传感器探测时重点监视次序是:敌、不明、我。其中敌方的威胁度最大,故隶属度最大,其他依次减小。
目标类型:目标类型有战斗机、轰炸机等各类飞机以及各种导弹等,不同的目标对我方的威胁程度截然不同,一般威胁程度越高的隶属度越大,非隶属度越小。部分目标赋值具体如下页表1所示。
目标速度:目标飞行速度越大,威胁程度越高,则对应的隶属度越大,非隶属度则越小。
目标航向:目标航行的方向与目标和防空区域中心连线的夹角越小,目标的攻击意图越明显,目标的威胁度越大,隶属度则越大,非隶属度则越小。
目标机动方式:指相对于防空区域的机动方式,一般分为巡航、盘旋、俯冲。其中俯冲的攻击意图最明显,目标的威胁度最大,相对应的隶属度就最大,非隶属度则最小。此外,盘旋威胁度次之,巡航最小。

表1 目标类型隶属度和非隶属度赋值表
目标距离:目标距离是指目标与防空区域边界的距离,目标距离越小,目标的威胁度越高,相对应的隶属度就越大,非隶属度就越小。
目标飞临时间:飞临时间是指目标到达防空火力发射区近界的时间,其值越小,武器系统和战术决策的准备时间越短,威胁度就越高,隶属度就越大,非隶属度则越小。
除此之外,为更加符合实际战场环境,还需要考虑目标的火控需求、目标的抗干扰能力等。
2.2 影响因素的权重求解
影响因素的权重未知势必会影响目标优先级排序方案的准确性,为得到准确的排序结果,确定各影响因素的权重大小是必不可少的工作。若所有目标在某因素下的属性值差异越小,则说明该因素影响作用越小,反之,如果某因素对所有目标差异值越大,则说明该因素影响作用越大。因此,从对目标优先级排序影响程度的角度考虑,目标影响因素的属性值差异越大,则赋予越大的权重。如果所有目标在某影响因素下的属性值没有差异,则说明影响因素对目标优先级排序不起作用,可令其权值为0。
定义3[7]:设A1=([a1,b1],[c1,d1]),A2=(([a2,b2],[c2,d2])为任意两个区间直觉模糊数,则定义两个区间模糊数之间的距离的计算方法为:


对于其中一个目标优先级影响因素Qj来说,定义Dik(ωj)为目标Ai与除Ai本身之外的目标之间的距离和为:
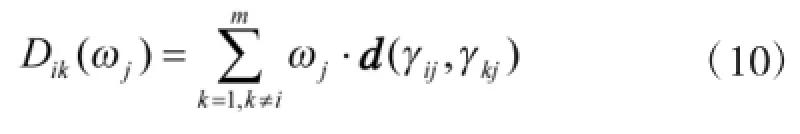
进一步,对于影响目标优先级一个因素Qj,定义所有目标与除本身之外的目标之间的总距离和为:
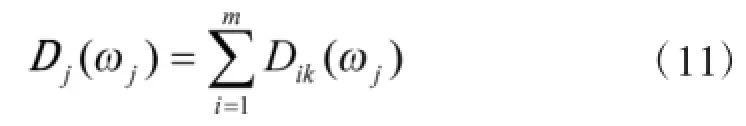
根据上述权重求解问题分析可知,权向量ωj的选取应该使得所有影响因素下所有目标总的区间直觉模糊数的距离值之和最大。因此,构造目标函数为:
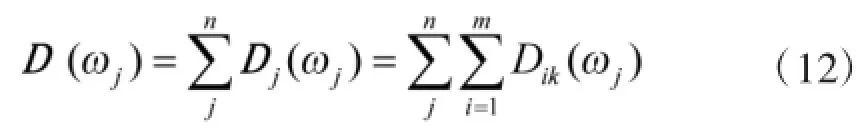
从而使得目标属性权重ωj的求解等价于求解如下最优化模型:
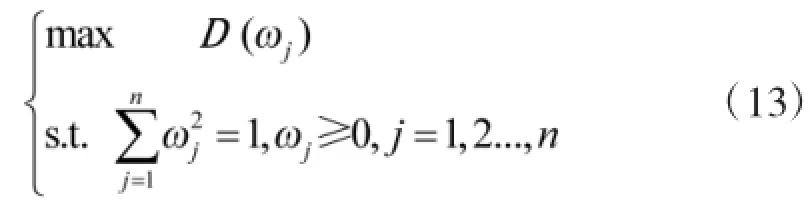
通过对D(ωj)构造拉格朗日函数,求导并做归一化处理可得目标影响因素的权重计算公式为。

到此,通过对目标威胁度影响因素的差异性度量,使得区间直觉模糊集距离最大化,求出了各影响因素的权重。同时为使决策结果更加的符合战场环境,可结合历史经验和咨询相关专家得到各影响因素的合理权重,使决策结果更加准确。
3 基于区间直觉模糊集的目标优先级求解算法
区间直觉模糊集的隶属度、非隶属度和犹豫度,代表着决策者对目标方案的支持、反对和中立,故可以利用此特性来解决多属性的目标决策问题。区间直觉模糊集的得分函数和精确函数类似于统计学中的均值与方差,其值又直接反应了目标方案的本质特性,因此,也可以根据其值对目标优先级进行排序。算法具体步骤如下:
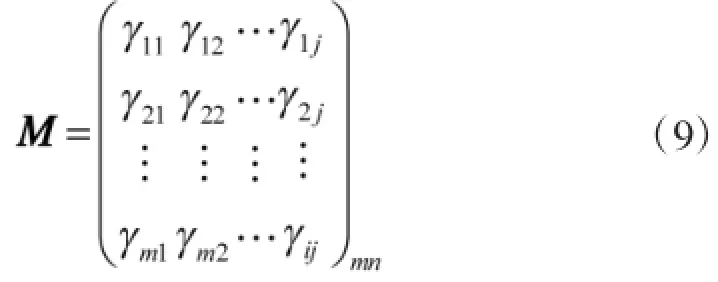
Step1:把传感器所测量的数据依据量化标准计算得出决策矩阵M;
Step2:在各影响因素权重未知的情况下,需先依据M和式(14)求得各影响因素权重ωj,j=1,2,…,n;
Step3:依据各影响因素权重ωj,j=1,2,…,n和M,利用IITFN-WAA算子求出综合加权决策矩阵:
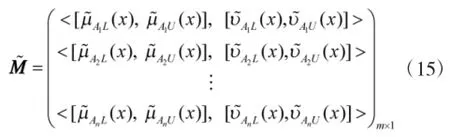
Step4:依据改进的得分函数计算公式,求得分函数S(Ai)和精确函数H(Ai)。
Step5:依据数据分析结果,得分函数值越大的对应目标的目标优先级越高,如果得分函数一样时,精确函数值越大的对应目标的目标优先级越高。其中S(Ai),H(Ai)分别按式(6)和(7)来计算。
4 案例分析
假设在某一战场环境下,雷达探测到4个敌方目标A1,A2,A3,A4。考虑目标的4个属性参数:Q1目标的类型,Q2目标的速度(m/s),Q3目标的距离(km),Q4目标的航向(°)。通过地面防空传感器获取的目标参数如表2所示。根据基于区间直觉模糊集的目标优先级求解方法进行目标优先级排序,具体求解步骤如下:

表2 目标属性参数表
Step1:根据实际目标参数得到基于区间直觉模糊集的决策矩阵M,如表3所示。

表3 目标在各影响因素下的隶属度和非隶属度的区间直觉模糊集表示
Step2:为使决策结果更加符合实际战场环境,依据专家经验得到各影响因素的权重依次为:ω1=0.34,ω2=0.28,ω3=0.18,ω4=0.20;
Step3:根据决策矩阵利用IITFN-WAA算子求得综合加权决策矩阵,具体见表4所示。

表4 目标综合区间直觉模糊集
Step4:根据式(5)和式(6)求得得分函数和精确函数值,具体见表5所示。
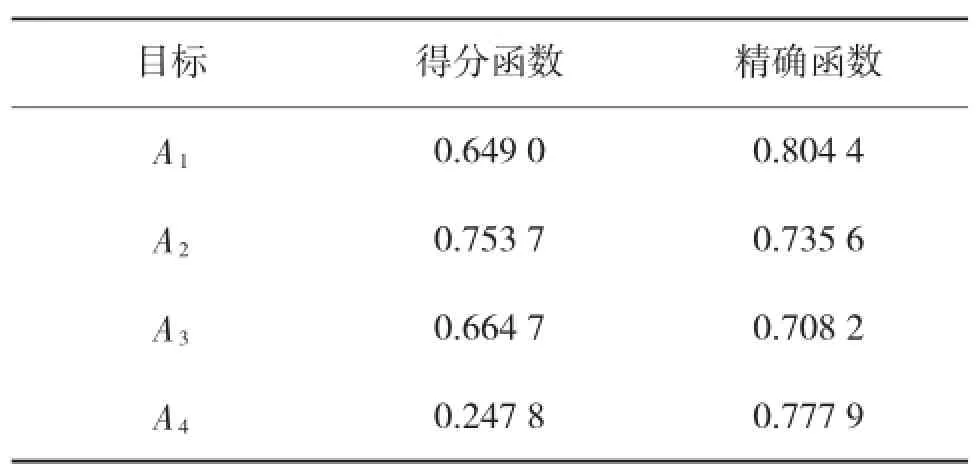
表5 目标得分函数和精确函数值
Step5:由得分函数可得S(A2)>S(A3)>S(A1)>S(A4),故目标的优先级顺序应该是:A2A3A1A4,即目标2的威胁度最高,其次是目标3和目标1,威胁度最低的是目标4。
结合实际的仿真场景,轰炸机相对于其他飞行物对防区的威胁度最高,直升机最低,战斗机与巡航导弹居中。仿真结果与实际战场环境相符,验证了该算法的有效性。
5 结论
本文针对复杂防空作战环境下多目标威胁度难以科学准确评估的问题,为更准确地处理战场上的模糊多变信息,提出了基于区间直觉模糊集理论的目标威胁度评估和优先级求解算法,其中对得分函数和精确函数进行了改进,考虑犹豫度信息对决策结果的影响,使得决策结果更准确并扩大了适用范围。所提算法在复杂战场环境下有了更强的适用性,对优化整个地面防空武器系统中的多传感器资源管理有着重要的作用。
该理论在多传感器资源管理领域还要很大的研究空间,下一步的研究工作可从以下两个方面展开:①深层次分析目标影响因素与目标优先级之间的非线性关系;②研究基于多传感器信息融合的目标优先级求解算法。
[1]王峰,潘泉,高全学,等.一种基于神经网络的目标优先级确定方法[J].电光与控制,2003,10(4):38-41.
[2]杨健,高文逸,刘军.一种基于贝叶斯网络的威胁评估方法[J].解放军理工大学学报(自然科学版),2010,11(1):43-48.
[3]ATANASSOV K.Intuitionistic fuzzy sets[J].Fuzzy Sets and Systems,1986,20(1):87-96.
[4]陈志旺,陈林,杨七,等.用区间直觉模糊集方法对属性权重未知的群求解其多属性决策[J].控制理论与应用,2014,39(8):1025-1033.
[5]ATANASSOV K.Operators over interval valued intuitionistic fuzzy sets[J].Fuzzy Sets and Systems,1994,64(2):159-174.
[6]徐泽水.区间直觉模糊信息的集成方法及其在决策中的应用[J].控制与决策,2007,22(2):215-219.
[7]童俊,单甘霖.基于Vague集的TOPSIS法求解目标优先级[J].火力与指挥控制,2012,37(5):140-143,147.
A Method of Target Priority Based on Interval Valued Intuitionistic Fuzzy Set
XU Gong-guo,DUAN Xiu-sheng,LI Sheng-jun
(Ordnance Engineering College,Shijiazhuang 050003,China)
Aiming at the problem of multi-object priority level being hard to be solved in complex air defense battlefield environment,the assessment method of target priority is proposed based on interval valued intuitionistic fuzzy set.Firstly,the influence factors of the target priority and the nonlinear relationship between the influence factors and the target priority are analyzed.Secondly,the score function and accuracy function of interval valued intuitionistic fuzzy set are improved with thinking about the hesitating information,and the algorithm of target priority based on the score function and accuracy function is proposed.Finally,simulation example verifies the effectiveness of the proposed algorithm.
targets priority,threat level,interval valued intuitionistic fuzzy set,score function,accuracy function
E917;TP391
A
1002-0640(2016)12-0050-04
2015-10-05
2015-12-17
军内科研基金重点资助项目(ZS2015070132A12009)
徐公国(1990-),男,山东滕州人,硕士研究生。研究方向:传感器管理与信息融合。

