VNS和SA相结合的指挥控制资源部署*

胡诗骏，姚佩阳，孙昱，李锴

（空军工程大学信息与导航学院，西安710077）

VNS和SA相结合的指挥控制资源部署*

胡诗骏，姚佩阳，孙昱，李锴

（空军工程大学信息与导航学院，西安710077）

针对指挥控制资源部署问题，引入任务复杂度来定义决策实体的工作负载，并建立以最小化决策实体工作负载的均方根为目标的优化模型。针对传统的层次聚类法容易陷入局部最优，提出了一种变邻域搜索（Variable Neighborhood Search，VNS）和模拟退火（Simulated Annealing，SA）相结合的具有全局性的求解方法，使用VNS进行全局寻优，使用SA对VNS中的邻域进行局部寻优。最后通过一个联合作战案例的平台调度方案，验证了所提方法的优越性。

资源部署，决策实体，任务复杂度，层次聚类法，变邻域搜索

0 引言

指挥控制资源部署问题［1-2］就是依据平台资源调度方案（即决策什么平台在什么时间去执行什么任务），将各个平台进行分组，为每一个分组配置一个决策实体，实质上这是一个平台聚类问题，也是三阶段设计方法第二阶段所要研究的内容——组织协作网的设计。一个良好的平台分组减少了决策实体之间不必要的交互协作，提高组织的运作效率，反之则增加了决策实体的工作负载，降低了组织运作效率［3］。

层次聚类法［4］是解决指挥控制资源部署问题的较普遍的方法。文献［5］提出了基于最小化工作负载合并原则的层次聚类法；文献［6］提出了基于最小化矢量距离合并规则的层次聚类法；文献［5-6］均以所控制的平台数量来定义内部工作负载，以协作完成的任务数量作为外部协作负载，不能将平台和任务两个不同的概念经过简单的相加来定义工作负载，对此文献［7］以任务的执行时间来衡量工作负载，设计了N-best备选策略来减小搜索空间，提出了基于最小化工作负载均方根的改进层次聚类法。层次聚类法都是以某种规则进行层次递进式的两两合并，产生的解是短视的，不一定能获得全局最优解。

本文引入任务复杂度来重新定义工作负载，并且针对层次聚类法的短视性，引入变邻域搜索［8-9］和模拟退火算法［10-11］这两种全局性算法，获得所求解问题的最优解。

1 问题的数学描述

1.1 基本概念

①决策实体（Decision-makers，DM）：联合作战的指挥官，通过所控制的平台资源来完成作战任务，其集合记为DM={DM1，DM2，…，DMD}，D为可配置的决策实体数目。

②平台（Platform，P）：决策实体所控制的物力资源实体，记平台集为P={P1，P2，…，PQ}，Q为平台的数目。

③任务（Task，T）：部队为完成预定的作战目的所执行的任务，由作战使命分解形成，通常由决策实体控制的平台资源协作完成，记任务集T={T1，T2，…，TN}，N为任务数量。任务Tn所需要的资源能力需求Pren=（Rn1，Rn2，…，RnL），Rnl［11］（l=1，2，…，L）是指成功执行Tn所需第l种资源能力的大小；任务激烈度［12］Sdn，即任务对抗的激烈程度，通常Sdk∈{0，1，2，3，4，5，6，7，8，9}。

④组织协作网：如图1所示，以两个决策实体、5个平台和两个作战任务的指挥控制组织来直观地认识组织协作网。

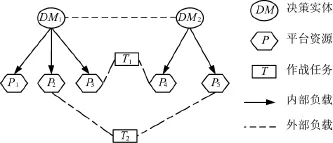
图1 组织协作网

1.2 变量定义

①平台-任务分配矩阵PT。即若平台Pm被分配执行任务Tn，则PTm×n=1；否则PTm×n=0。该矩阵已由平台资源调度问题［12］求出，在指挥控制资源部署问题中是输入变量。

②平台-决策实体聚类矩阵PDM。即若决策实体DMd控制平台Pm，则PDMm×d=1；否则PDMm×d=0。该矩阵也是本文所要求解的矩阵。

③任务-决策实体分配矩阵TDM。即若决策实体DMd协作完成任务Tn，则TDMn×d=1；否则TDMn×d=0。

④决策实体之间的协作变量COdbn。即若决策实体DMd和决策实体DMb协作完成任务Tn，则COdbn=1；否则COdbn=0。

1.3 决策实体的工作负载定义

决策实体的工作负载由两部分组成，即内部工作负载和外部协作负载。内部工作负载是决策实体控制的平台资源来完成任务产生的工作负载，外部协作负载是决策实体之间协作完成某一任务产生的工作负载。在以往的决策实体工作负载定义时，通常将决策实体控制的平台资源数量作为内部负载，将协作完成的任务数作为外部协作负载，以两者的简单相加作为总的工作负载。这种定义方式简单地将平台和任务这两个不相关的概念相加，无法真正反映决策实体的工作负载。

本文考虑到任务的激烈程度、执行时间及功能需求3个方面因素对决策实体工作负载的影响，定义任务的复杂度作为负载的测度。记任务Tn的复杂度为CxDn，其定义如下：

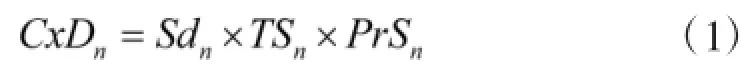
其中，Sdn为任务Tn的激烈度，TSn为任务Tn的执行时间因素，PrSn为任务Tn的功能需求因素。

任务Tn的执行时间因素定义为任务Tn的执行时间与整个使命完成时间的比值，即

其中，tn为任务Tn的执行时间，tsum为整个使命的完成时间。

任务Tn的功能需求因素定义为任务Tn的资源能力需求中的各项能力与完成整个使命所需该项能力比值的均值，即

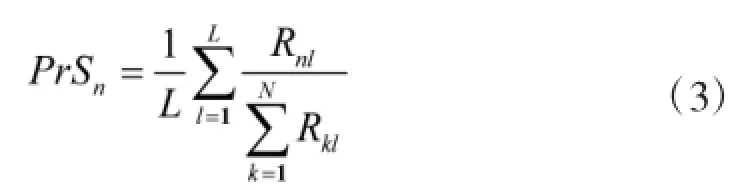
1.3.1 决策实体的内部工作负载

决策实体DMd通过所控制平台完成任务产生的工作负载定义为其内部工作负载，记为，即

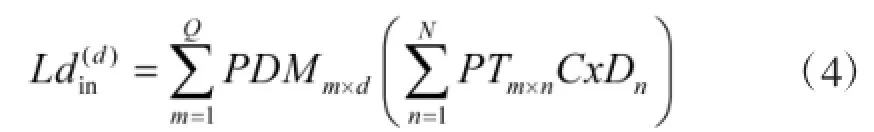
1.3.2 决策实体的外部协作负载

决策实体DMd与其他决策实体协作完成任务产生的工作负载定义为其外部协作负载，记为，即

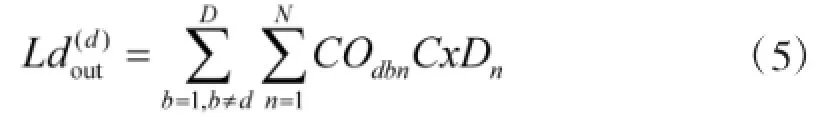
1.3.3 决策实体的工作负载

决策实体DMd的工作负载定义为其内部工作负载与外部协作负载的加权和，记为，即：

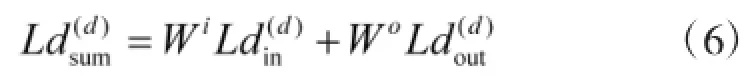
其中，Wi为内部工作负载的权重，Wo为外部协作负载的权重。

1.4 数学模型的建立

①决策实体可以控制多个平台，但某个平台只能是受某个决策实体控制，即：

②每个决策实体都至少控制一个平台资源，否则没有存在意义，即：

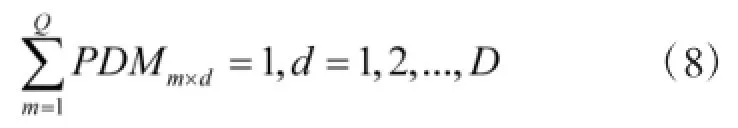
③只有当TDMn×d=1且TDMn×b=1时，COdbn=1。由此可得：

综合式（9）和式（10）可得：

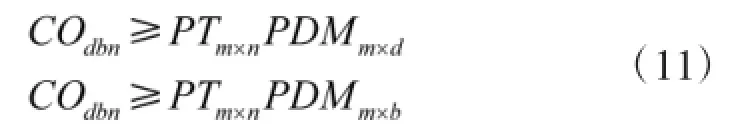
④指挥控制资源部署设计的目标主要是在减小整个C2组织总工作负载的同时，兼顾各个决策实体的工作负载尽可能差异小。本文采用所有决策实体工作负载的均方根作为目标函数的测度，则目标函数为：

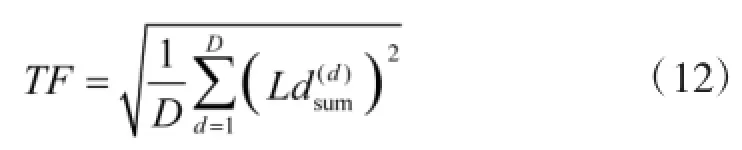
综合以上分析，指挥控制资源部署问题的数学模型如下：

2 问题求解

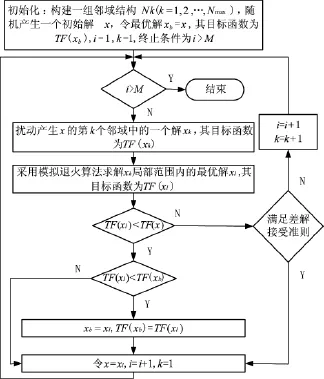
针对式（8）所描述的数学模型，采用在变邻域搜索方法中嵌入模拟退火算法来求解指挥控制资源部署问题，其流程图如图2所示。

2.1 变邻域搜索算法

变邻域搜索算法的基本思路如图3所示。

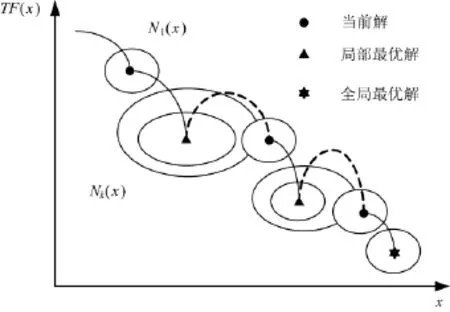
图3 VNS的基本思路图

由上图可以直观地发现变邻域搜索正是通过邻域的扩展来进行全局搜索，达到全局最优。VNS算法的具体步骤如下：

Step1初始化。设计一组邻域结构Nk（k=1，2，…，Nmax），随机生成一个初始解x；

Step2令迭代计数器i=1，直至i＞M；

Step3令k=1，直至k=Nmax；

Step3.1扰动产生的x第k个邻域中的一个点xl；

Step3.2找出点xl周围的局部最优解点xb；

Step3.3解更新。若局部最优解优于当前解，则令x=xb，k=1，转Step3；否则k=k+1；

Step4令i=i+1，转Step2。

2.1.1 初始解构造

针对设置的D个决策实体，Q个平台资源，随机产生Q个1～D之间的随机整数，组成一组排列数作为初始解x，即（x1，x2，…，xk，…，xQ）。

由于产生的随机数可能存在不可行解，会产生很多不必要的搜索，为了缩小搜索空间，提出如下修正策略：

Step1初始化。令D个决策实体控制的平台资源数目分别为y1，y2，…，yD，并设初始所有决策实体控制数目均为0，令i=1，k=1；

Step2若xk=yi，则yi=yi+1，k=k+1；否则k=k+1；

Step3若k＞Q+1，则i=i+1，转Step4；否则转Step2；

Step4若i＞D+1，则转Step5；否则转Step2；

Step5令a=1；

Step6若ya=0，从决策实体控制数目不为0对应的初始解x中的位置用a取代原先的值，a=a+1；否则a=a+1；

Step7若a＞D+1，则转Step8；否则转Step6；

Step8输出新的初始解x'。

2.1.2 邻域构造

扰动机制的设计也就是邻域结构的构造，本文引入遗传中变异、交叉的思想来构建两种可供随机选择的邻域结构：变异邻域和交叉邻域。

变异邻域就是在当前解中随机一个位于1～Q之间的数作为需要变异的位置，然后随机一个位于1～D之间的数取代该位置原先的值，如此产生的解集，如图4所示。

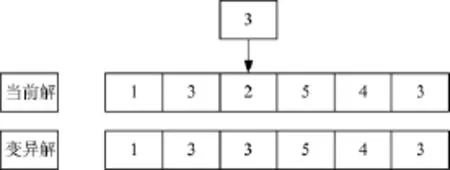
图4 变异邻域图

交叉邻域就是在当前解中随机出两个不同的位于1～Q之间的数作为待交叉的两个位置，将这两个位置的值进行互换，如此产生的解集，如图5所示。

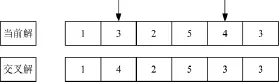
图5 交叉邻域图

2.1.3 基于模拟退火的局部搜索

本章变邻域搜索算法采用模拟退火进行局部搜索，不仅能获得局部最优解，还能一定程度跳出局部最优，其步骤如下：

Step1变邻域搜索中求得的xk作为模拟退火的初始解，设置初始温度T0、终止温度Tf、温度更新参数a、Markov链长度为M，令T=T0，i=1，局部最优解xl=xk；

Step2由解xl扰动产生新解xn，令B=TF（xn）-TF（xk），若B＜0，则xk=xn；否则按一定概率准则接受xn为当前解；

Step3C=TF（xn）-TF（xl），若C＜0，则xl=xn；

Step4令i=i+1，直至i＞M，转Step2；

Step5令T=aT，直至T＞Tf，转Step2。

1）扰动机制

采用遗传中变异的思想进行扰动产生新解，与变邻域搜索邻域构造中的第一个变异邻域相同。

2）概率准则

对于T温度下解xl扰动产生新解xn，令B=TF（xn）-TF（xk），若B＜0，则xk=xn；否则按式（14）准则接受xn为当前解。

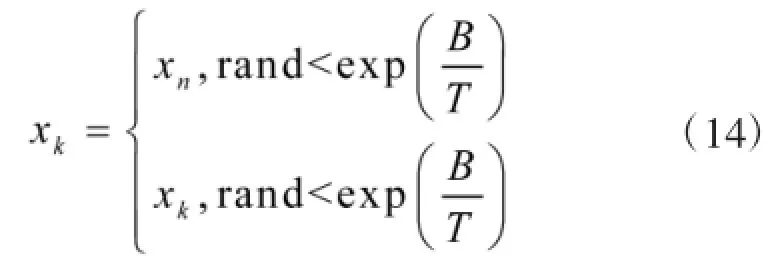
2.1.4 劣解接受准则

图2中，当TF（xl）＜TF（x）不满足时，此时按如下解接受准则接受劣解，以防止变邻域搜索过早陷入局部最优。

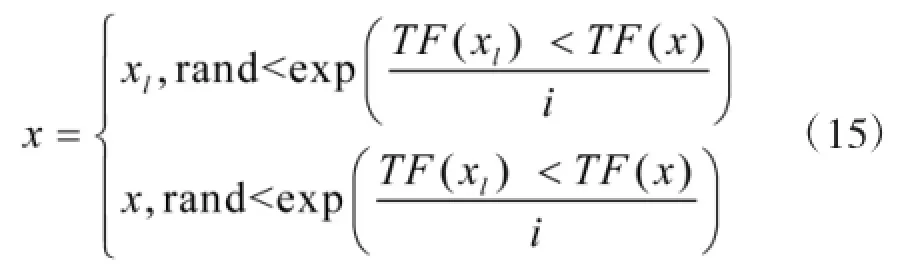
其中，i为图2中的迭代计数器。

3 算例分析

为了验证所提方法的优越性，以文献［3］中的联合登岛作战为例，以其中的一个平台调度方案为输入，取各个任务对抗的激烈程度为Sdn=1（n=1，2，…，18），进行仿真实验，平台调度方案如下页图6所示。

仿真实验1当Wi=0.4，Wo=0.6，决策实体数目为D=6时，分别使用基于最小矢量距离的层次聚类法、基于N-best备选策略合并规则的层次聚类法和本文提出的方法进行算例求解，其结果如下页表1所示。

从表1中可以看出，本文所提的VNS和SA相结合的平台聚类方法比基于矢量距离的层次聚类法、基于N-best备选策略的层次聚类法的结果都要好，总的工作负载更小，同时各决策实体的工作负载比较均衡。

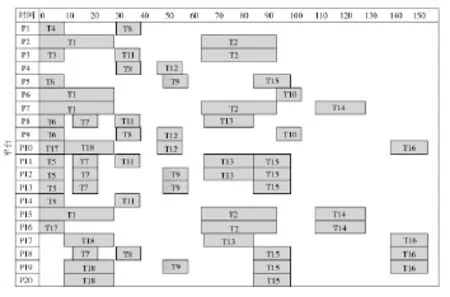
图6 平台资源调度方案甘特图

表1 3种不同方法的平台聚类结果

仿真实验2当Wi=0.4，Wo=0.6，决策实体数目D取1～15时，分别使用基于最小矢量距离的层次聚类法、基于N-best备选策略合并规则的层次聚类法和本文提出的方法进行算例求解，其结果如图7所示。

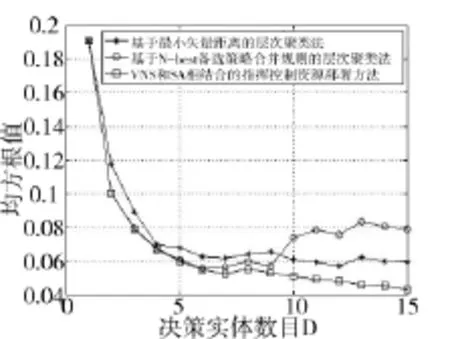
图7 3种算法均方根随决策实体数目变化曲线

由图7可知，随着决策实体数目D的变化，VNS和SA相结合的平台聚类方法所求得的结果中各决策实体工作负载的均方根值都要比基于最小矢量距离的层次聚类法和基于N-best备选策略合并规则的层次聚类法所求出的值小，也就是说本文采用的方法总工作负载较小，同时各决策实体工作负载更加均衡。同时，对于决策实体大于9时，基于N-best备选策略合并规则的层次聚类法的效果相对来说反而更差，而本文设计方法始终能找到更好的解。

仿真实验3当决策实体数目为D=6，在0.05到0.5之间取不同值时，分别使用基于最小矢量距离的层次聚类法、基于N-best备选策略合并规则的层次聚类法和本文提出的方法进行算例求解，其结果如图8所示。

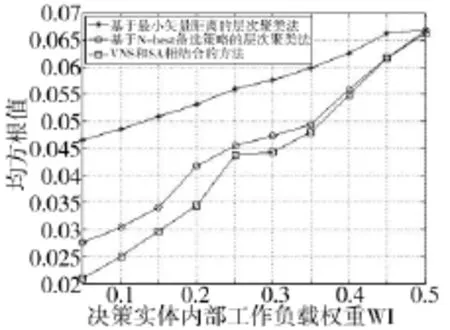
图8 3种算法均方根随内部工作负载变化曲线

图8中，内部工作负载Wi从0.05以0.05的间隔逐渐增加到0.5，可以看出当内部工作负载权重逐渐增大的情况下，外部协作负载权重逐渐减小，相对于基于矢量距离的层次聚类法，后两种方法有较大的优势，但优势越来越不明显。这是因为总的内部工作负载都是相同的，通过减小外部协作负载来实现平台聚类优化。因此，随着外部协作负载的权重越来越小，后两种效果也随之不明显。同时，本文设计的全局性的VNS和SA相结合的平台聚类方法在效果上始终优于基于N-best备选策略合并规则的层次聚类法。

4 结论

指挥控制资源部署问题作为三阶段设计方法的第二阶段，是指挥控制组织设计中的重要工作之一。本文通过引入任务复杂度进行工作负载的定义，建立以最小化所有决策实体的均方根为目标函数的数学模型，同时提出了一种VNS和SA相结合的具有全局性的问题求解方法。针对联合登岛作战案例中的一个平台调度方案进行了实验仿真，仿真结果验证了所提方法的优越性。

［1］BUI H，HAN X，MANDAL S，et al.Optimization-based decision support algorithms for a team-in-the-loop planning experiment［C］//Proceedings of the 2009 IEEE International Conference on Systems，Man，and Cybernetics.TX：IEEE Press，2009：4684-4689.

［2］YAN J J，DUANMU Z Y，ZHOU X M，et al.A plan-driven dynamic reconfiguration mechanism for C2 communities ofinterest［C］//Proceedings of the 15th International Command and Control Research and Technology Symposium，2010.

［3］阳东升，张维明，刘忠，等.指控组织设计方法［M］.北京：国防工业出版社，2010.

［4］KASHEF R，KAMEL M S.Cooperative clustering［J］.Pattern Recognition，2010，43（6）：2315-2329.

［5］LEVCHUK G M，LEVCHUK Y N，LUO J，et al.Normative design of organizations-PartII：Organizational structure［J］. IEEE Transactions on Systems，Man，and Cybernetics—Part A：Systems and Humans，2002，32（3）：360-375.

［6］刘宏芳，阳东升，刘忠，等.兵力编成裁剪算法研究：决策结点裁剪［J］.系统工程理论与实践，2007，27（5）：106-112.

［7］周翔翔，姚佩阳，王欣.基于改进层次聚类法的指挥控制资源部署［J］.系统工程与电子技术，2012，34（3）：523-528.

［8］BOUHMALA N，HJELMERVIK K，VERGAARD K I.A generalized variable neighborhood search for combinatorial optimization problems［J］.Electronic Notes in Discrete Mathematics，2015，32（3）：360-375.

［9］董红宇，黄敏，王兴伟，等.变邻域搜索算法综述［J］.控制工程，2009，16（S2）：1-5.

［10］SUMAN B，KUMAR P.A survey of simulated annealing as a tool for single and multiobjective optimization［J］.Journal of theOperationalResearchSociety，2006，57（10）：1143-1160（18）.

［11］朱颢东，钟勇.一种改进的模拟退火算法［J］.计算机技术与发展，2009，19（6）：32-35.

［12］李小全，詹海洋，程懿.面向任务的炮兵指挥控制建模仿真［J］.火力与指挥控制，2014，39（8）：34-37.

［13］胡诗骏，姚佩阳，孙昱，等.DLA和NGA结合的平台资源调度方法［J］.空军工程大学学报（自然科学版），2015，16（2）：82-86.

Command and Control Resource Deployment Based on VNS and SA

HU Shi-jun，YAO Pei-yang，SUN Yu，LI Kai
（School of Information and Navigation，Air Force Engineering University，Xi’an 710077，China）

To solve the command and control resource deployment problem，the complexity of a task is introduced to measure decision-makers’workload and a mathematical model whose objective function features the minimization of root mean square value of the decision-makers’workload is built. Aimed at the hierarchical clustering algorithm that is liable to plunge into local optimum，this paper presents an approach with overall importance to solve the problem based on Variable Neighborhood Search（VNS）and Simulated Annealing（SA）.VNS is used to find out global optimum with using SA to find local optimum in the neighborhood.Finally，the superiority of this algorithm are illuminated through a platform resource scheduling scheme which is in a case of joint campaign.

resource deployment，decision-makers，complexity of a task，hierarchical clustering algorithm，variable neighborhood search

TP391.9

A

1002-0640（2016）12-0020-05

2015-10-07

2015-12-13

国家自然科学基金资助项目（61573017）

胡诗骏（1990-），男，浙江杭州人，硕士研究生。研究方向：组织结构模型设计。