欠驱动再入飞行器的抗饱和姿态控制器设计*

李宪强，周军

（1.北京空间技术研制试验中心，北京100094；2.西北工业大学精确制导与控制研究所，西安710072）

欠驱动再入飞行器的抗饱和姿态控制器设计*

李宪强1，周军2

（1.北京空间技术研制试验中心，北京100094；2.西北工业大学精确制导与控制研究所，西安710072）

针对只有两个舵的欠驱动再入飞行器，设计了具有抗饱和功能的姿态跟踪控制器。控制器的设计过程中，首先将姿态运动学与动力学模型分解成慢回路和欠驱动的快回路，然后分别针对快回路和慢回路设计了超扭曲滑模控制器和分层滑模控制器，最后通过仿真验证了该方法的有效性。

欠驱动，再入飞行器，饱和，分层滑模

1 INTRODUCTION

Under-actuated systems are characterized by the fact that they have fewer actuators than the degree of freedom to be controlled［1］.As to most of existing reentry vehicles，the rudder-type control surface may fail when they fly at large angle of attack，thus leading to under-actuation of vehicles.

At present，the research results on attitude controller design of under-actuated reentry vehicle mainly cover literatures［2-4］.All such literatures firstly select the proper output variables through using output redefinition［5］，then dynamic inversion and other control methods with better robustness are employed，so as to finally realize local stability of attitude tracking system of under-actuated reentry vehicle.But the system stability under actuator saturation is not mentioned in literatures［2-4］.During actual flight，reentry vehicle is often subject to actuator saturation，which will result in the performance reduction of control system，even system instability.For this reason，it is of great significance to study attitude tracking of under-actuated reentry ve hicle under input saturation.To track desired attitude of under-actuated reentry vehicle，a kind of attitude tracking controller is designed for under-actuated reentry vehicle with input saturation in this paper on the basis ofsuper-twisting sliding mode control theory，hierarchical sliding mode control theory and adaptive control theory.

2 MODELANALYSISANDPROBLEM FORMULATION

The attitude kinematics and dynamics of the under-actuated reentry vehicle with only two inputs can be expressed as following［2］

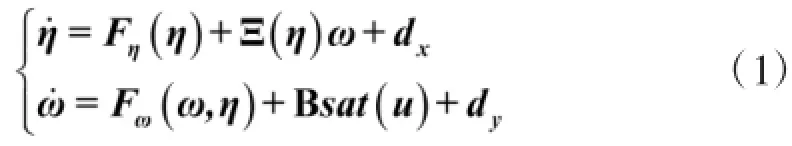
Based on widely accepted time-scale separation assumption，equation（1）can be divided into slow-loop subsystem and fast-loop subsystem as following：

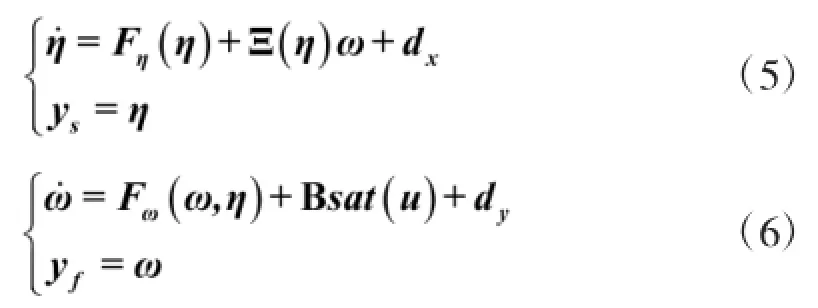
In equation（6），the freedom degree of control variables of fast-loop subsystem is smaller than that of the control system，so it is a typical under-actuated system. When ω is selected as output，equation（6）shows a typical non-minimum phase system.And unacceptable internal dynamics may be caused when the control methods based on dynamic inversion is adopted.

3 CONTROLLER DESIGN

During the design，a slow subsystem controller and a fast subsystem controller are designed separately.

3.1 CONTROLLER DESIGN FOR SLOW-LOOP SUBSYSTEM

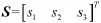
Theorem 3.1 If selecting the sliding mode surface S described as formula（8）and the controller in formula（9），for the system formula（7），

Proof By calculating the derivative of S in formula（8），and substituting formula（7），we can get

By calculating the derivative of formula（9）and substituting it into formula（10），we can get

Take

3.2 DESIGN OF FAST-LOOP SUBSYSTEM CONTROLLER

where δe_eqand δα_eqdenote the equivalent control，δe_sand δα_sdenote the sliding mode switching control.

Selecting the total sliding mode surface as［23-24］

Lemma 3.1［7］When stotalin formula（19）converges to the origin，zi（i=1，2，3）will also converge to the origin at the same time.

Differentiating the both sides of the formula（19），and noting formulas（1），（14）and（18），we can obtain

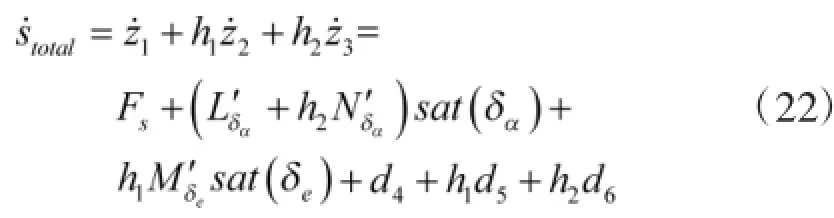
Substituting formulas（16）and（17）into formula（22），we have

The equivalent control can be choosed as following

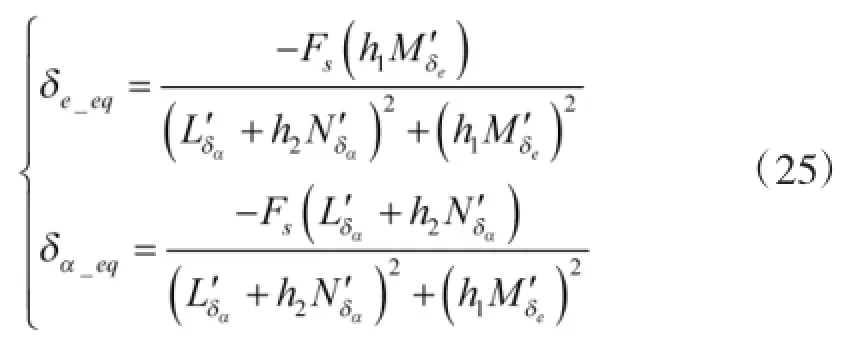
Substitutingformula（25）intoformula（23），wehave

Theorem 3.2 Formula（14）will be stable under the control of below controller（formulas（27）-（28）），i.e.

wherein，δe_eqand δα_eqare denoted as（25），

and the adaptation update laws are

where，p1and p2are the positive constants to be selected.

Proof For the plant（14），we choose the following candidate Lyapunov function

Differentiating V（t）with respect to time t，and substituting formula（23）into the derivative of V（t），we obtain

From formula（32），we have

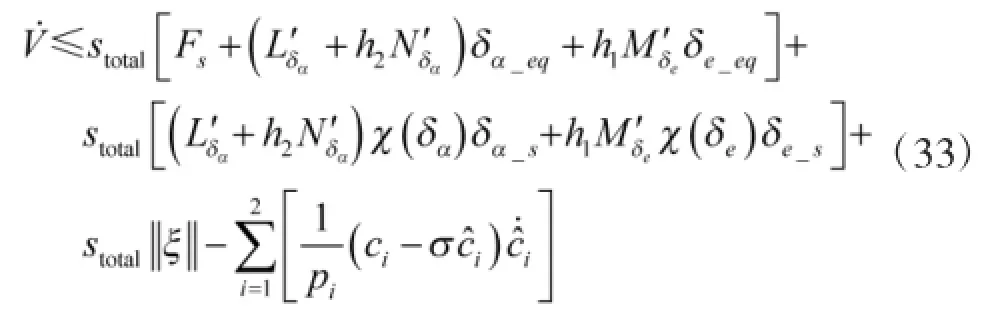
substituting the formula（25）into inequality（33），yields

according to assumption 3.3 and formula（34），we

can obtain

substitutingformula（28）intoinequality（35），yields

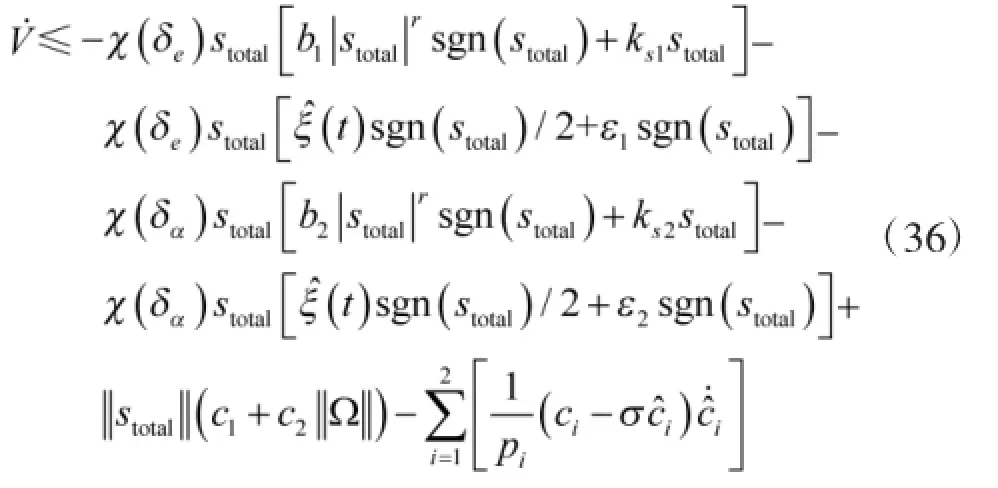
According to assumption 3.2 and inequality（36），we can obtain

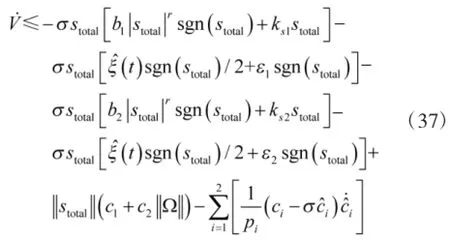
substitutingformula（29）intoinequality（37），yields

According to formula（30），we can obtain

substituting formulas（29）and（39）into inequality（38），yields

then，we can get

4 SIMULATION RESEARCH

This section focuses on performance verification of control system subjected to input saturation.Parameters forsimulationareselectedas：K1=3I3，K2=1.5I3，ks1=ks2=2.1，ε1=ε2=0.05，b1=b2=0.27，r=0.75，adaptive

parameters：p1=1.52 and p2=2.13，initial adaptive value: cˆ1（0）=1，cˆ2（0）=1.Corresponding simulation results are shown in Fig.1-Fig.5.

Under input saturation（Fig.1），the angle of sideslip can still be effectively restrained within 3°（Fig.3）and the tracking effect of the angle of attack and sideslip angle is satisfying.And Fig.5 show that，the adaptive parameters can also be stabilized.In summary，forunderactuatedreentryvehicle，the controller designed shows good performance under input saturation.

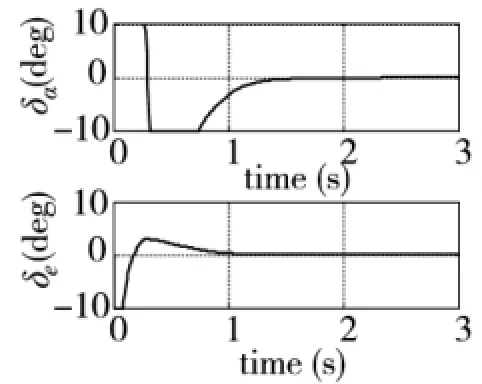
Fig.1 Control input with saturation.

Fig.2 Attack-angle α responses under input saturation.

Fig.3 Side-slip angle β responses under input saturation.

Fig.4 Bank-angle γvresponses under no input saturation.

5 CONCLUSION

The paper introduces a control method of un-reduce actuators configured，thus lowering system mass and cost.In addition，it shows great practical significance for solving system stability issues in case of control input saturation and model disturbance.

Fig.5 The estimated parameters under input saturation.

［1］QIAN D，YI J，ZHAO D.Hierarchical sliding mode control for a class of SIMO under-actuated systems［J］.Control and Cybernetics，2008，37（1）：159-175.

［2］WALLNER E M，WELL K H.Attitude control of a reentry vehicle with internal dynamics［J］.Journal of Guidance，Control，and Dynamics，2003，26（6）：846-854.

［3］ITO D，GEORGIE J，VALASEK J，et al.Reentry vehicle flight controls designguidelines：dynamic inversion［C］// NASA/TP—2002-210771，2002.

［4］SHIN J，BALAS G，PACKARD A.Worst-case analysis of the X-38 crew return vehicle flight control system［J］.Journal of Guidance，Control，and Dynamics，2008，24（2）：261-269.

［5］KIM S G，TAHK M J.Output-redefinition based on robust zero dynamics［C］//In Proceedings of AIAA Guidance，Navigation，and Control Conference，Boston，1998.

［6］JAIME A M.Strict lyapunov functions for the super-twisting algorithm［J］.IEEE Transactions on Automatic Control，2012，57（4）：1035-1040.

［7］BAO Y，LI J，XIE J，et al.On hierarchical sliding mode control of underactuated TORA system［C］//In Proceedings of the 10th World Congress on Intelligent Control and Automation，Beijing，China，2012.

［8］TIGGES M A.Preliminary v-201 entry flight profile with landing site precision，cycle-8［M］.NASA V-201-NOI 175，1998.

［9］VOEGT S，BURKHARDT J，MULLER S，et al.CREDITS-model and algorithm description［M］.Astrium Space Infrastructure，TET-DASA-18-SW-2185，Germany，1999.

Attitude Tracking of the Under-actuated Reentry Vehicle with Actuator Saturation

LI Xian-qiang1，ZHOU Jun2
（1.Beijing Manufacture and Experiments Center of Space Technology，Beijing 100094，China；
2.Institute of Precision Guidance and Control，Northwestern Polytechnical University，Xi’an 710072，China）

In this paper，an attitude tracking controller for the under-actuated reentry vehicle with only two actuators is designed in the presence of actuator saturation and disturbance.During design of the controller，the attitude kinematics and dynamics model of under-actuated reentry vehicle is firstly divided into a slow-loop subsystem and a under-actuated fast-loop subsystem.And then a supertwisting sliding mode controller and an adaptive hierarchical sliding mode controller are designed separately for the slow-loop subsystem and fast-loop subsystem.Finally，the validation of the method is verified through simulation.

under-actuated，reentry vehicle，saturation，hierarchical sliding mode

TJ765.3

A

1002-0640（2016）12-0015-05

2015-11-18

2015-12-26

国家自然科学基金资助项目（61403028）

李宪强（1986-），男，河南濮阳人，博士。研究方向：导航、制导与控制。