用好“问题串”,打开学生思维的张力
——以“分数的基本性质”为例
□江苏省太仓市弇山小学 叶萍
用好“问题串”,打开学生思维的张力
——以“分数的基本性质”为例
□江苏省太仓市弇山小学 叶萍
【课前思考】“分数的基本性质”是小学数学第十册第六单元的第一课时。学习本内容之前,学生已清楚理解分数的意义,明确分数与除法的关系、商不变规律等知识,这些都为本课学习做了知识上的铺垫。本课在小学数学学习中起着承前启后、举足轻重的作用,它既与整数除法的商不变规律有着内在的联系,也是后面进一步学习约分、通分、分数计算的基础。
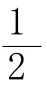
【案例】
一、搭建“脚手架”
“脚手架”是一种辅助工具,“君子善假于物”,我们要善于借力。借助学生已学过的“商不变性质”,用推理、验证的方法帮助学生学习分数基本性质,从而搭好了一个漂亮的“脚手架”。
【教学片段1】
师:交流前置作业:
(1)()÷3=2÷6=3÷()
你是根据除法的()规律填写的,请把这个规律写出来。
(2)根据分数与除法的关系,你觉得分数与除法一样,也有什么规律?
生1:1÷3=2÷6=3÷9,我是根据除法的商不变规律填写的,被除数和除数同时乘或除以相同的数(0除外),商不变。
生2:我赞同他的观点,我也是根据除法的商不变规律填写的。
生3:我来解决第二个问题,我们已经知道:被除数相当于分数的分子,除数相当于分数的分母。因此我可以推导出:分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变。
师:推理是我们学习的好帮手,能使我们举一反三,掌握新知识。刚才这位同学的推理,你们认同吗?怎样来验证?
【反思】学生不是一张白纸,但这张纸上到底涂抹了什么“底色”,勾勒了哪些“线条”?“君子善假于物。”在平时的教学中我们要善于借力,教学不能无视学生已有的知识经验,简单强硬地从外部对学生实施知识的“填灌”,而应当把学生原有的知识经验作为新知识的生长点,引导他们从原有的知识经验基础上生长新的知识经验,搭好一个漂亮的“脚手架”。教学中引导学生根据分数与除法的关系初步推理出分数的基本性质,这既尊重了学生原有的知识基础,又让学生合情推理,掌握学法,引导学生学会学习。
二、用好“问题串”
数学是思维的体操,问题是数学的心脏。好的数学问题有两个标准:既能反映当前学习内容的本质,又在学生思维能力的最近发展区。
【教学片段2】
师:对于分数基本性质,你们还有哪些问题想问?
生1:分数的大小不变,分数的意义变了吗?
师:你们赞同吗:
生:同意。
(师继续提问)
生:分数的分子和分母同是乘或除以同一个数,这个数可以除0以外的任何数吗?包括小数和分数吗?
生:没有。
师:那可以是除0以外的任何数吗?
生:可以的。
师:继续提问。
生(基础比较差的):分数的分子和分母同时加或减同一个数,分数的大小变吗?
【反思】质疑是学习、思考和探索中非常重要的一个环节,我们学校倡导“核心问题”教学,其核心目标之一就是培养学生发现问题、提出问题的能力。在出示分数基本性质之后,让学生说说对于分数基本性质还有什么问题想问。在其他班试上时,学生提不出问题,只好采用传统老师提问的方式。而在这节课,由于这个班的学生一年级我带起来的,平时教学时一直鼓励学生敢于主动质疑,当老师问道:“你还有问题吗?”一只只小手像雨后春笋举起来,一个个问题接踵而至,“分数的大小不变,分数的意义变了吗?”“分数的分子和分母同是乘或除以同一个数,这个数可以是小数、分数吗?”“分数的分子和分母同时加或减同一个数,分数的大小变吗?”学生提的问题是多么到位,多么精到,这些问题令我惊喜,“这些问题谁能解决?”教师的又一问激起了学生的大讨论,学生通过举例子的方法的方法一一解决自己提出的问题,他们问得精彩,答得同样精彩。看来,课堂上放一放真能收获很多。
三、打开思维张力
【教学片段3】
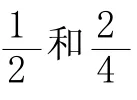

课堂中,我以“问题串”为主线,串联起学生的思维链,通过问题的层层递进,一些极富挑战的问题激发了学生的探究欲望,使学生完整地经历了一个“再创造”的学习过程,认知由简单到复杂,从低层到高层,从朦胧到清楚,使得课堂教学连续不断地从一个高潮到另一个高潮,一石激起千层浪,激活了学生思维的“一池春水”,打开了学生的思维张力。

