走好矫治数学学困生的第一步

□江苏省苏州工业园区唯亭学校 陈祥

走好矫治数学学困生的第一步

□江苏省苏州工业园区唯亭学校 陈祥

《伊索寓言》中有这样一则故事：一个暴风雪的日子，有一个穷人到富人家讨饭。

“滚开!”富人家的仆人凶狠地说，“不要来打搅我家主人。”

穷人不紧不慢地应道：“只要让我进去，在府上的火炉旁烤干衣服就行了。”仆人听穷人这么说，以为这不需要花费什么，勉强让穷人进去了。

穷人进屋后，到厨房向厨娘借了一个小锅，他要“煮点石头汤喝”。

“石头汤！”厨娘奇怪的很，心想：“我倒想看看你怎样煮你的石头汤。”于是递给穷人一个锅，这时，只见穷人把刚才路边拣到的那块石头洗净后放在锅里煮了起来。

“可是，你总得放点盐吧？”厨娘边问边给了穷人一点盐，然后又往锅里放了点豌豆、香菜，最后干脆把案板能收拾到的零星碎肉末一起放到锅里。

到此，你也许能猜到，穷人后来把石头捞出来扔掉，美美地喝了一锅热乎乎的肉末菜汤。

这个故事对我们的数学教育是很有指导意义的。

学生到了初中阶段，由于各种各样的原因，出现了两极分化的现象，在数学上，尤为明显！在数学上掉队的孩子都表现为对数学缺乏兴趣，对自己没有信心！我曾经做过一个简单的调查，我问学生（初三）你那么多回家作业，你能否告诉我你回家后做作业的先后次序？结果很有意思，我调查了23个后进生，15个学生将数学放在最后一个完成，6个学生将数学放在倒数第2个（最后做物理），2个学生没有回答！我还问了这几个同学这样做的原因，答案很一致——“数学太难，我们不会做！”这个答案让我深思，我想正常情况下，在读题以前是无法判断一道数学题的难易程度及自己能否完成！但这些同学在作业之前，就已经“拒绝数学”，就开始暗示自己没有能力做好数学作业。这样怎么能学好数学？我们应该怎样扭转这种局面？上述寓言给了我们一点启示——

穷人为什么能达到目的（喝到肉汤）？我想他走好了第一步：向仆人提了一个仆人认为自己很容易办到的要求，从而进了房子！

那我们应该怎样达到目的（矫治数学学困生）？我想第一步也很关键！那我们的第一步是什么呢？我想也应该向学生提出学生自己认为容易办到或者自己“跳一跳就能够着”的要求，而要达到这个效果我个人认为首先应该培养学生的信心，增强学生的自我效能感。

一、提高学生的数学学业自我效能感

自我效能感，指一个人对自己在某一活动领域中操作能力的评价，即个体在某一行为操作前对自己能够在什么水平上完成该行为活动所具有的信念、判断或主体自我感受。我们将数学学业的自我效能感界定为：人们在数学学习这一特定情境中，对自己的数学学业能力的自信程度，即自己在面临数学学习这一具体任务时，是否相信或有多大程度相信自己有足够的能力去完成学业任务。它并非一个人真实的数学能力，而是一个人对自己数学能力的评估和信心，是在数学活动中对自己的数学能力进行衡量和评价的结果，而这种结果又转而调节人们对数学活动的选择、投入努力的大小，以及遇到困难时的坚持性，并且决定他们在数学活动中所表现出的能力。那么我们应如何提高学生的自我效能感呢？笔者认为要提高学生（特别是学困生）的自我效能感，可以在布置学生任务时，提供给学生“先行组织者”。这和新教材所提倡的情境教学不谋而合，因为情境也是一种先行组织者。

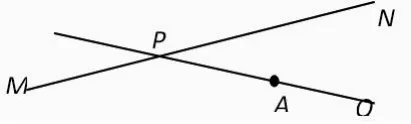
例如，在初中教解直角三角形时，有这样一道题目：如图，公路MN与公路PQ在点P处交汇，且∠PQN=30°，点A处有一所中学，AP=150m。假设拖拉机行驶时，周围100m以内会受到噪音的影响，那么拖拉机在公路MN上沿PN方向行驶时，学校是否受到噪音影响？说明理由。

这一题是一道比较典型的解直角三角形的题目，要求学生自己将实际问题数学化，构建直角三角形，虽然计算不复杂，但中下水平的同学却无法正确地数学化。因此在给这道题前，我提供了这样的材料，提出以下问题：

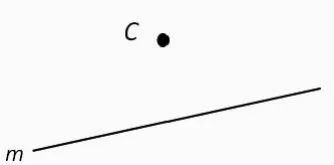
（1）什么叫点到直线的距离？你能在图中作出来吗？

（2）你能在直线m上找出一个点到C的距离最近？

这两个问题将有助于学生知识的迁移，使中下水平的学生也可以自己作出辅助线，构建直角三角形，而该题的直角三角形的模型又相对简单，一般水平的学生能自己利用模型解决问题，从而提高其自我效能感！

二、激发和培养学生的数学学习的兴趣

穷人能喝到肉汤的另外一个重要原因是他成功地激发了厨娘的兴趣，使她自觉自愿地帮助穷人。那么到我们教学上也一样，我们要到达目的，也需要激发和培养学生的数学学习兴趣。

我有个学生，在我接这个班的时候（初二），他的班主任老师就告诉我他的数学是很薄弱的，对他没有成绩上的要求。我看了看他初一的成绩单，数学30分刚出头！

我开始对他放低要求，例如二次根式的乘法化简计算只要求能化简最简单的（如等），而且要求其每次做作业时只要将被开方数用短除法分解为质因数的积，而其余复杂的、带字母的，我对他均不要求了。同时，我为他恶补了初一的一元一次方程解法和合并同类项。

我的出发点：简单的一元一次方程解法和合并同类项，智力正常的学生通过努力都能掌握，是符合他的能力水平的，而且这两块在整个初中数学中是比较重要的，是进一步学习的基石。而对初二的新知识，则根据他的能力，学习最基本的和最本质的东西。经过我一段时间的训练，虽然他的考试成绩还是很差，但慢慢地在进步了，从一开始的完全瞎填到“就算错也错得有点眉目”，甚至有几题能做对，同时我也在等待能在数学学业上表扬他的契机。

契机出现了，出现在几何上！在讲授“全等三角形”的时候，我发现他能自己独立地利用有关知识做简单的证明题，虽然因果关系写得不是很好，但证明的思路及主体结构都很好。我利用投影仪将他的解答向全班讲了一下，并帮他修改了几个小错误，在全班面前好好地表扬了他一番！

几何有进步，但代数进步却缓慢。我却越来越放松，因为他对数学已经有了点信心和兴趣，在代数上也比以前肯花时间，终于在“一元二次方程”的解法上有了突破。虽然他现在的成绩还是不理想，但挂科的次数已大大减少，比以前无论从学习数学的成绩、态度、信心、兴趣等方面都有了长足的进步

试想，要是穷人一开始就对仆人说：“给我一碗肉汤吧！”会有什么结果呢？因此，我们对学生如果一味地指责，一上来就向他提出超过他能力水平的要求，那么我们能得到什么结果？结果可想而知！所以我们不妨对数学学困生适当放低要求，通过使他们感受成功，增强他们的信心，培养他们的兴趣，从而迈出矫治数学学困生的第一步！