把握解题窍门，攻破数学难题

江苏省大丰高级中学高三（16）班 王柏铭

把握解题窍门，攻破数学难题

江苏省大丰高级中学高三（16）班 王柏铭

在数学解题中，有人欢喜有人愁，有人左思右想，绞尽脑汁，仍百思不得其解；有人转换角度，另辟蹊径，豁然开朗；有人乘势而下，顺水推舟，水到渠成。同一道数学题，有人思路明确，推理清晰，解法精妙独到，简单易懂；有人却思维僵化，不知变通，解法呆板单一，繁琐复杂。究其根源在于学生对解题“窍门”的把握。因此，在平时解题学习和复习过程中，同学们要注意把握解题窍门，攻破数学难题。

一、从数学概念和性质分析中探求解题窍门，破解数学难题

数学概念和性质是数学解题的重要基础。在许多数学问题中，无论从题设条件、所求结论还是直观图象都或多或少地隐含着某种特征。在解题时，若能善于观察，用心捕捉这些特征，联想到与之相应的概念和性质，往往可以快速地找到解题的突破口，从而使问题迎刃而解。

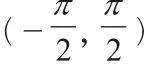
下面证明这样的k是唯一存在的。

假设a1+a27=a2+a26=a3+a25=…=a13+a15=2a14＞0，由单调奇函数性质可知，

f（a1）+f（a27） ＞0，f（a2）+f（a26） ＞0，f（a3）+f（a25） ＞0，…，f（a13）+f（a15） ＞0，又因为f（a14） ＞0，所以f（a1）+f（a2）+f（a3）+…+f（a27） ＞0，这与题设条件相冲突。同时若a14＜0时，则有f（a1）+f（a2）+f（a3）+…+f（a27） ＜0，同样也与题设条件相冲突。综上所述，若则有f（a1）+f（a2）+f（a3）+…+f（a27）=0时，则当且仅当k=14时，f（ak）=0。

【评注】本题主要考查学生对函数奇偶性、单调性以及等差数列性质的综合运用能力。在解本题时，只有把握了函数奇偶性、单调性以及等差数列性质这一解题“窍门”，才能使问题得以有效解答。

二、从特殊与一般的转化中发现解题窍门，攻克数学难题

唯物辩证法告诉我们，事物之间是既有共性又有个性的关系。在数学学习过程中，我们对概念、公式、定理、法则的认识大多是从特殊开始，由特殊情形归纳出一般结论，然后再运用一般性结论解决数学问题。在某种条件下，特殊与一般两种思想可以相互转化，因此，在平时数学解题中，我们要予以重视，善于观察，灵活运用，从而高效解题。

例2 （2014年高考·江苏卷·第20题）设数列｛an｝的前N项和为Sn，若对任意正整数n，总存在正整数m，使得Sn=am，则称数列｛an｝是“H数列”。设数列｛an｝为等差数列，其首项a1=1，公差d＜0，若数列｛an｝是“H数列”，求d的值。

【分析】本题有两种解题思路：其一是借助特殊化思想由特殊情形得出结论后再去验证一般情形成立；其二是从公差d＜0出发，由Sn=am得出一般结论成立再去验证特殊情形也成立。

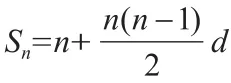
【解法2】由“H数列”的定义，Sn=ak，得1+（1+d）=1+（m-1）d，即（m-2）d=1。因为d＜0，m为正整数，所以上式只有在m=1时才能成立，此时d=-1。

【评注】本题旨在考查学生对数列知识的掌握情况以及灵活运用特殊与一般转化思想解决问题的能力。在解本题过程中，学生若能从特殊与一般的转化中发现解题窍门，往往可以使问题得以快速、有效、准确地解答出来。

三、从求解和求证的目标推理中明晰解题窍门，攻破数学难题

在数学解题中，许多学生习惯于从已知条件或原因中推理出所求结论，而不习惯于从所求结论中一步步推理出原始条件或原因。实际上，对于某些数学问题，若能突破思维定式，反其道而思之或行之，从所求解或证明的结论目标入手，进行推理、猜想、分析，往往会收到意想不到的效果。

例3 定义在R上的单调函数f（x）满足f（3）=log23定义，且对任意x，y∈R都有f（x+y）=f（x）+f（y）。

（1）求证：f（x）为奇函数；

（2）若f（k·3x）+f（3x-9x-2）＜0对任意x∈R恒成立，求实数k的取值范围。

【分析】要想证明f（x）为奇函数，需证明对任意的x都有f（-x）=-f（x）成立。在式子f（x+y）=f（x）+f（y）中，令y=-x，可得f（0）=f（x）+f（-x）。此时又出现一个新的问题——求f（0）的值。令x=y=0，可得f（0）=0，从而f（x）为奇函数得到证明。

（1）f（x+y）=f（x）+f（y）（x，y∈R）①

令x=y=0，代入式①中，得f（0+0）=f（0）+f（0），即f（0）=0

令y=-x，代入①中，得f（x-x）=f（x）+f（-x）

又f（0）=0，则有0=f（x）+f（-x），即f（-x）=-f（x）对于任意x∈R都成立，

故f（x）为奇函数。

（2）从所求证的目标进行分析推理，可以得出以下解法：

即u的最小值为2-1，要使对x∈R， 不等式-1恒成立，

只要使k＜2-1即可。

总之，数学解题方法灵活多样，同学们要善于观察，巧抓题目特征，把握解题窍门，灵活运用数学方法，从而快速、有效解题。