巧用奇函数的性质解数学题

湖南省岳阳市第十五中学326班 李博亚

巧用奇函数的性质解数学题

湖南省岳阳市第十五中学326班 李博亚

函数是高中数学中的一个重要内容，也是难点之一。主要体现在函数思想的运用，而掌握函数的一个重要手段就是分析函数的性质。从函数的性质入手来求解数学问题，也是解决函数问题的非常适用的工具。而我们在解决函数问题时往往容易忽视的地方主要体现在：一是忽视从函数的本质特性入手，如定义域、对应法则、函数的单调性、奇偶性等。二是容易忽视分析题设所给式子的结构特征。因此，我们可以从奇函数的定义出发，证明出奇函数的性质，函数的性质是函数的灵魂。在解答一些类似很抽象的问题时，我们先从函数的性质入手，认识这个函数的本质特征，巧用其性质来解答，可以达到事半功倍的作用。

一、奇函数的定义及性质

在我们的教材中奇函数是这样定义的：设函数y=f（x）的定义域为D,如果对D内的任意一个x,都有x∈D,且-f(x)=f(-x),则这个函数叫做奇函数。其中的关键词有“D内的任意一个x”、“都有”“-f(x)=f(-x)”。用数形结合的思想来理解奇函数的定义就是：奇函数的定义域关于原点对称，其图形关于原点成中心对称图形。从这个定义出发，我们很容易证明奇函数具有如下四个性质：

性质1 对定义在区间D上是单调递增奇函数f（x），如果a,b∈D，

性质2 已知定义在区间D上的单调递减奇函数f（x），如果a,b∈D，

性质3 已知在区间D上的单调奇函数f（x），如果a,b∈D，

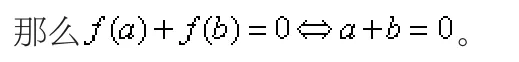
性质4 如果奇函数f（x）是定义在D上的奇函数，且有最大值M，那么f（x）的最小值为-M，反之亦然。即如果定义在D上的奇函数f（x）有最大值M和最小值N，那么M+N=0。

二、奇函数性质应用举例

奇函数的定义及性质看似简单容易，但要巧妙地运用它来解题，还是有一定难度的。首先我们要掌握题设的结构特征，就是函数值和自变量之间的关系，分析函数的性质，判断其奇偶性，巧用这些性质解答题目可以达到事半功倍的作用，下面举例说明。

分析：初看此题，首先就想到它是一个分式不等式，脑海中就浮现出分式不等式的解题基本思路：转化成整式不等式求解。但冷静一看不等式前面两个式子和后面的似乎有某种神似。运用函数中整体代换的思想就不难想到可以用构造法构造一个奇函数f（x）=x3+5x，从而使问题简化。

解后随笔： 这道题如果运用分式不等式的常规解法思想去把其转化为整式不等式求解，则不仅要解一个6次高次不等式，而且难度很大，很难解出。这里构造一个函数，并根据这个函数的奇函数性质求解，使问题得到简化，降低了运算难度。

解后随笔：这个题目，我们如果去列方程组求x和y的值，就会陷入解题的绝境。而根据题设中给出的两个式子在结构上的相似性，运用到函数中整体的思想，代换的思想，构造一个函数，再利用函数的性质解决就容易多了。

总而言之，我们还可以从定义出发，推导出奇函数的很多性质，在解题的过程中，如果能够熟练掌握这些性质，灵活运用，就可以达到开阔思路，简化过程的效果。