椭圆与双曲线焦点三角形面积的两个性质
2017-01-04 12:27潘剑儒
数学通报 2017年4期
潘剑儒
(成都师大一中高中部 610303)
数学教学以传授与培养思想方法进而提高数学素养与能力为根本目的,以不同的角度去探究熟悉的数学问题往往会有更精彩的方法或更新的发现.本文以“离心角”(参变量)为路径探索关于焦点三角形面积与外接圆半径R,内切圆半径r的关系.分别得到关于椭圆与双曲线焦点三角形面积的奇异性质.本文所用方法简单自然,结论奇异而且拓展空间大.
1 椭圆焦点三角形面积的性质
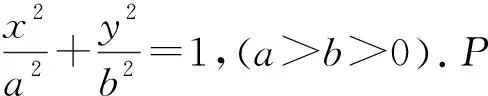
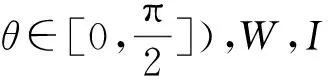
F1(-c,0),F2(c,0)分别是左右焦点,r1,r2分别为焦半径PF1,PF2的长.
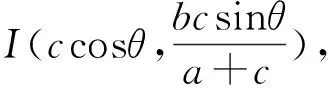
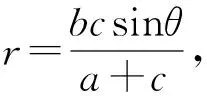
①
又由线段PF2的中垂线方程
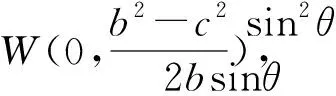
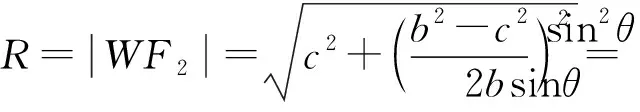
②
由圆锥曲线统一定义知
r1=a+ccosθ,r2=a-ccosθ,
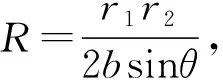

③
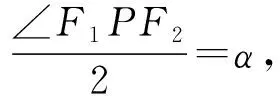
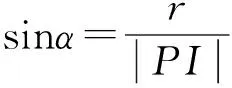
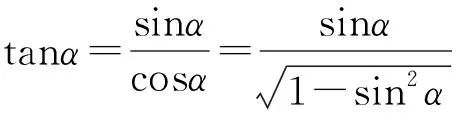

④

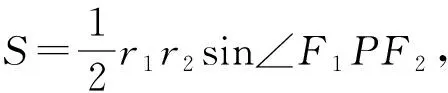
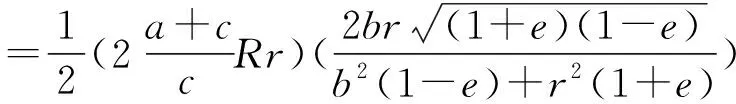
最后分母用均值不等式得
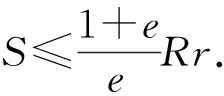
性质1证毕.
2 双曲线焦点三角形面积的性质
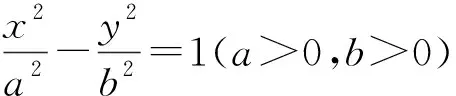
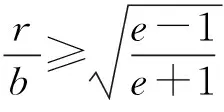
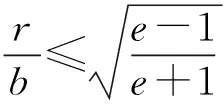
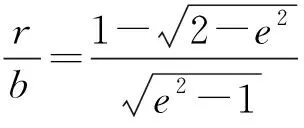
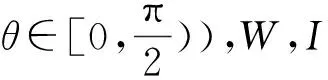
因线段PF2的中垂线方程为
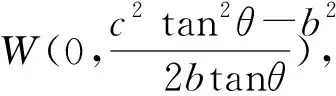
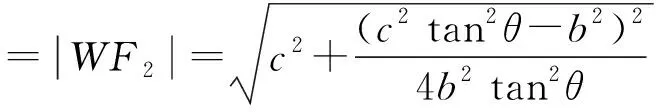
由圆锥曲线统一定义知
r1=csecθ+a,r2=csecθ-a,
则r1r2=c2(1+tan2θ)-a2=b2+c2tan2θ,
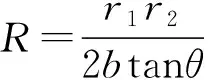
⑤
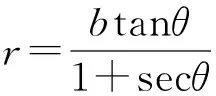
⑥
⑤与⑥式相乘得r1r2=2(1+secθ)Rr
⑦
由⑥两边平方整理得
r2(2+2secθ+tan2θ)=b2tan2θ,
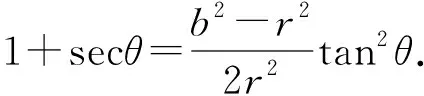
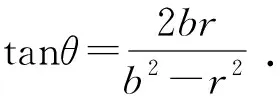
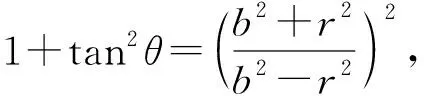

⑧
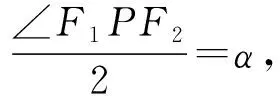
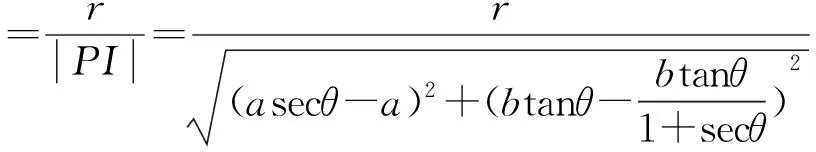
故sin∠F1PF2=sin2α=2sinαcosα
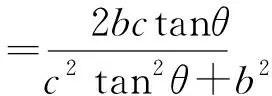
⑨
分母用均值不等式知S≤(1+secθ)Rr
⑩
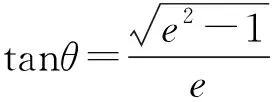


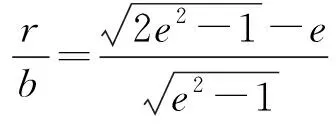

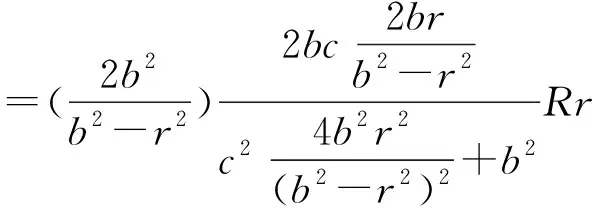
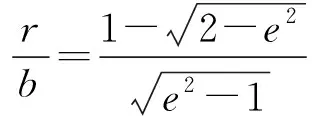
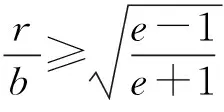
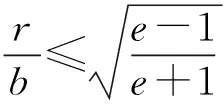
性质2证毕.
正所谓所行道路不同,则欣赏的风景不同,本文以“离心角”为路径,得到如此有趣的性质.从本文证明过程不难看出上述③、④、⑦、⑧等式也是椭圆与双曲线的有用性质,用这些性质可以得到相关更多奇异结论.作为抛砖引玉,最后给出下例两个问题,有趣的读者可根据本文的相关结论或推导思路解决.
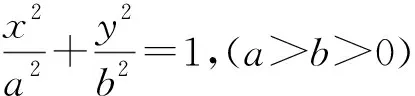
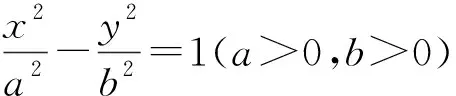
猜你喜欢
中学生数理化·七年级数学人教版(2021年11期)2021-12-06
中学生数理化·七年级数学人教版(2020年11期)2020-12-14
中学生数理化·七年级数学人教版(2019年11期)2019-09-10
教育教学论坛(2018年41期)2018-10-13
中学生数理化(高中版.高二数学)(2017年1期)2017-04-16
少儿美术·书法版(2016年4期)2016-11-02
学苑创造·B版(2015年6期)2015-07-01
中学数学杂志(2015年9期)2015-01-01
数学教学(2013年4期)2013-08-13
中学理科·综合版(2008年9期)2008-10-15

