圆锥曲线的两个重要结论及其应用
孔 磊
(山东省泗水县实验中学,273200)
圆锥曲线的两个重要结论及其应用
孔 磊
(山东省泗水县实验中学,273200)
圆锥曲线是高中数学的重要内容,也是高考的热点之一.在求解圆锥曲线的问题时,常规解法往往伴随较大的计算量,同学们大都感觉比较困难,成功率不高.但如果能在一些特定的情景中运用重要结论,则可以迅速认清问题本质,确定解题方向,便捷而准确地得到答案.
问题1设直线l与圆O相交于A,B两点,AB的中点为M,则OM⊥l.
这是初中时我们学习过的重要定理——垂径定理.如果将上述情境中的圆变为椭圆,结论是否依然成立?
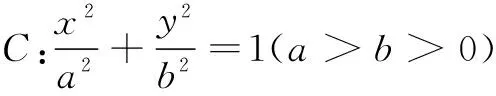
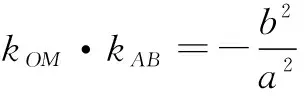
特别地,当b=a时,椭圆变为圆,kOM·kAB=-1,即OM⊥AB(垂径定理).
下面我们运用点差法给出结论1的证明.
设A(x1,y1),B(x2,y2),则
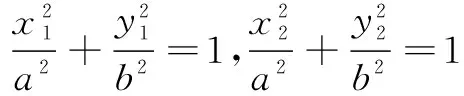

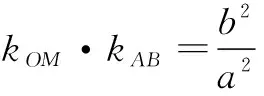
应用上述结论处理有关“中点弦”的问题会非常便捷.

解析本题的常规解法需要将直线方程与椭圆方程联立,再用根与系数的关系进行求解,或用点差法.而利用结论1,直接有
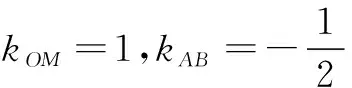
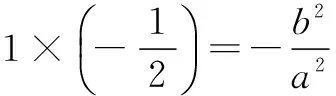
又a2=b2+c2,

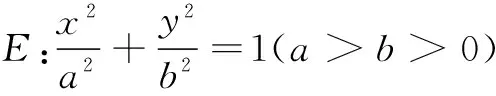
(1)求椭圆E的离心率;

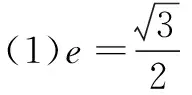
(2)由(1)知,椭圆E的方程为
x2+4y2=4b2.

利用结论1,有
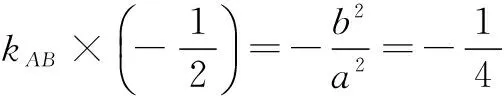
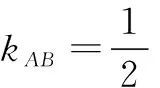
与椭圆E的方程x2+4y2=4b2联立,得
x2+4x+8-2b2=0,
∴ x1+x2=-4,x1x2=8-2b2.
由弦长公式,有
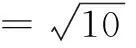
解得b2=3,故所求椭圆方程为

评注本题中椭圆与圆相交,注意到圆的直径是弦,而圆心是弦的中点,直接利用结论1,求出直线AB的斜率,从而大大简化了运算过程,提高了解题速度与准确率.
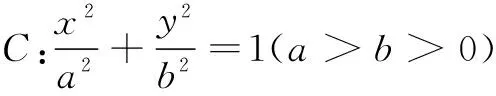

证明由椭圆定义,有
|PF1|+|PF2|=2a.
在∆F1PF2中,由余弦定理,得
|F1F2|2=|PF1|2+|PF2|2-2|PF1||PF2|cos θ =(|PF1|+|PF2|)2-2|PF1||PF2|(1+cos θ), 即4c2=4a2-2|PF1||PF2|(1+cos θ),
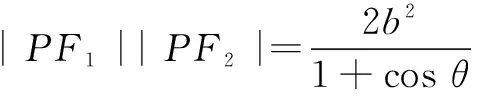

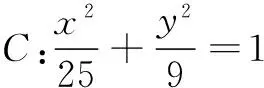
(1)∆F1PF2的面积;
(2)点P的坐标.
解析(1)由结论2,直接得
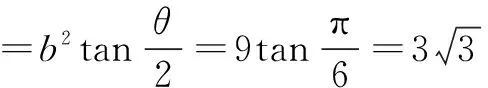
(2)利用等面积法,有


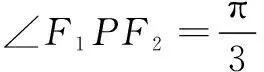
解析设椭圆方程为

双曲线方程为
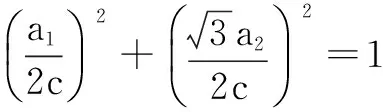
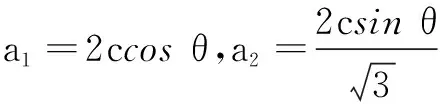

故答案选A.
评注本题利用结论2,直接得出b1与b2关系,再转化为a1,a2及c,再由三角换元得出答案.
通过以上几个例题,同学们可以看到,在求解圆锥曲线问题时,如果能在一些特定的情境中运用重要结论,则可以快速准确地得到答案.这就要求同学们在日常学习中,不仅要掌握解决问题的通用通法,也要重视这类重要结论的积累和运用,以不断提高我们解题的速度和准确率.

