一节基于选课走班的三角探究课
魏安龙
(江苏省南京外国语学校仙林分校,211100)
一节基于选课走班的三角探究课
魏安龙
(江苏省南京外国语学校仙林分校,211100)
选课走班是应新的高考模式而出现的一种新的教学方式.本文通过一节三角探究课的教学背景、教学目标与设计、教学反思等方面,力图反映出这种课堂的一些改革创新形式,为高中数学教学改革提供素材.
一、背景
我校在高一年级实行了选课走班的教育改革.其中数学的选课走班为每周一节,采取全年级学生自由选择,分层教学.教学内容以探究为主,从基础内容的探究开始,逐步深入.这种设计,可以适合各种不同层次的学生需求,为学生实现“全面而有个性的发展”提供了重要保证,同时为学校构建富有时代精神、体现多元开放、凸显办学特色以及多层次、可选择的学校课程体系,提供了重要保证.
根据江苏高考改革方案,2018年开始的高一年级将实行“3+3”的高考模式,届时所有的中学都要进行选课走班的教学.选课走班的数学教学,与目前的数学课堂有很大的差异,尊重学生是选课走班的数学课堂的重要特征.
高一数学课程三角知识有:必修4的任意角的三角函数及两角和与差的三角函数,必修5的解三角形.课程内容横跨两个模块两本教材,教学时间中间经过寒假跨过两个学期.在学情方面,高一学生数学学习能力并不是很好,对知识的融会贯通水平有限.为使学生更好地理解和掌握以上三角知识块,有必要开设三角内容综合的学习课程.
二、教学目标
(1)通过三角函数问题的学习和探究,让学生进一步理解三角函数的概念及基本性质;认识三角函数与实际生活及其它数学知识的紧密联系;进一步体会三角函数在解决具有周期变化规律问题中的作用.
(2)通过三角恒等变换问题的探究,让学生能合理运用公式及其变形,进行简单的恒等变换;进一步发展学生的推理能力和运算能力.
(3)通过解三角形问题的探究,让学生进一步认识和理解三角形中的边长与角度之间的数量关系,并能运用它们解决有关问题.
(4)学习重点难点:三角函数变换及性质、解三角形
三、探究情境设计
问题1上了两节课之后,时钟的时针转过的角α为多少度?多少弧度?如果时针的长为20 cm,时针扫过的图形面积为多少?
设计意图数学来源于生活,三角知识从角开始,弧度制是从三角计算到研究三角函数的重要过渡.问题从最为基础的知识起步,可以复习回顾与角有关的主要知识.
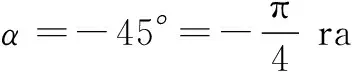
问题2对上面的α,如果角β终边所在直线经过点P(12,5)求tan(α+β)及cos(β-α)的值.
设计意图本题起点很低,涉及的三角知识比较多,起始于三角函数概念,落脚于两角和与差的三角函数,特别适合分层教学中的基础班学生.

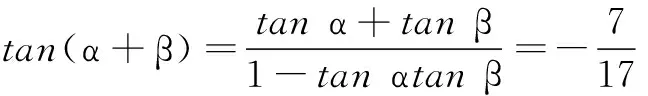
当角β在第一象限时,
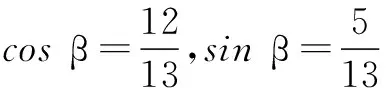


当角β在第三象限时,

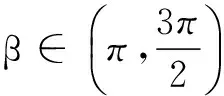
设计意图本题起点在前面问题的铺垫下是提高了许多,主要涉及两角和与差的三角知识,重点是角的变换.
解由β和β+γ的取值范围,知

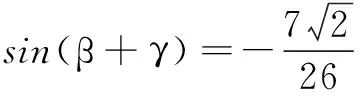




问题4如果分针经过12分钟转过的角为θ,
(1)求cos θcos 2θcos 3θcos 4θ;
(2)你会求cos θ的值吗?
设计意图三角函数有很多解题技巧,有些是三角函数中特有的,学生必须知道.本题(1)中的乘以1后循环使用二倍角公式的方法就是其中之一. 本题(2)是对三角函数公式的进一步拓展,具有探索性.
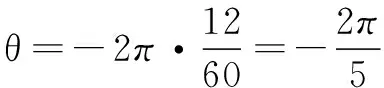
cos θcos 2θcos 3θcos 4θ
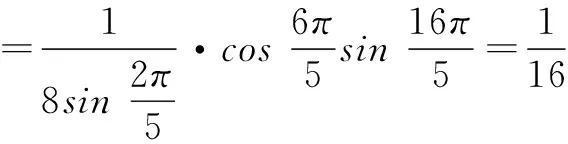
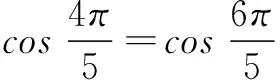
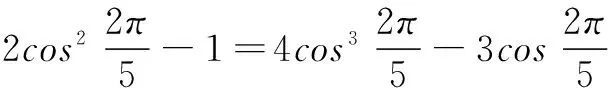
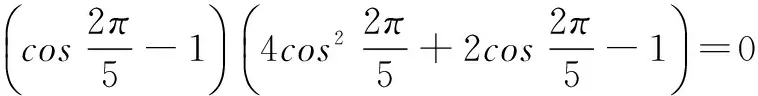

(1) 求函数f(x)的最小正周期;
(2) 求函数f(x)的单调减区间;

设计意图三角函数知识的联系比较广泛,在三角本身除计算方面的应用,另一个方面就是其函数的特性.以向量为载体的三角问题是常见的综合问题.通过本题的解决,一方面全面复习三角函数图象和性质的有关内容,另一方面体现三角函数与向量的综合.


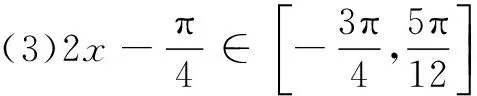


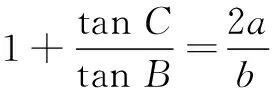
(1) 求角C的大小;

(3)若(a+b)2-c2=4,求3a+b的最小值.
设计意图本题主要是解三角形的探究问题,对于知识方面从特殊角三角函数值、同角三角函数基本关系到两角和与差的三角函数,正弦定理、余弦定理的应用.一个问题复习了整个三角的重点内容.
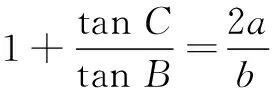
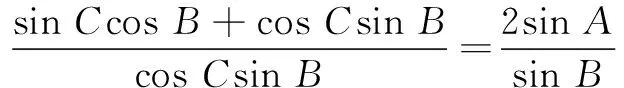
∵在∆ABC中,sin A≠0,sin B≠0,
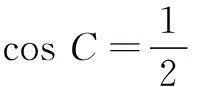

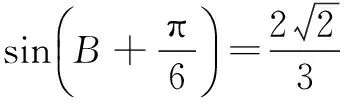
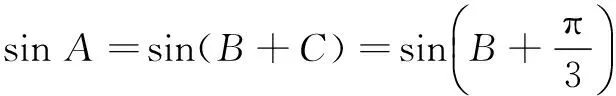

(3)∵(a+b)2-c2=4,
∴a2+b2-c2+2ab=4,
由余弦定理知2abcos C+2ab=4.

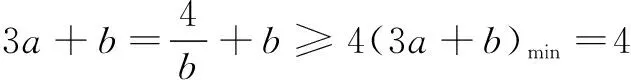
四、教学反思
1.好的选材是良好课堂的基础
《普通高中数学课程标准》指出,教材中素材的选取,首先要有助于反映相应数学内容的本质,有助于学生对数学的认识和理解,激发他们学习数学的兴趣,充分考虑学生的心理特征和认知水平.素材应具有基础性、典型性,内容设计要有一定的弹性.
本节课的6个问题,基础性方面体现得还可以,但是在体现三角知识的数学本质、有利于提高对三角内容的整体认识方面还有改进的可能.由于课堂时间和空间的限制,本设计没有涉及三角函数应用方面的实际问题,课堂容量偏大.课堂容量大的直接影响就是探究难以深入,课堂弹性空间小.
2.课堂是有意义学习的主阵地
奥苏贝尔的有意义学习理论认为, 有意义学习过程的实质,就是符号所代表的新知识与学习者认知结构中已有的适当观念建立非人为的和实质性的联系.其要求就是在教学时,要充分考虑学生已有的认知基础.
本节课的教学设计分别是从学生已有的角的概念、已有的任意角三角函数定义、已有的三角函数公式、已有的正弦定理余弦定理等知识出发,在学生自愿选择学习这一节课的意愿下,起始于生活中的时钟问题,充分尊重学生的认知规律,有利于理解知识本质,固化三角函数知识结构,教学效果比较好.
3.好的探究离不开好的引导者
探究课的主要目的是提高学生的学习兴趣,促进学生主动学习.落实在教学设计上,就是探究的问题是否具有好的探究效果;落实在课堂上,就是教师的教学艺术和引导学生探究的能力是否能够具有较好的吸引力.同一个问题,对于不同的老师、不同的学生、不同的学生基础,可能在探究的细致程度、知识生成方向等方面会有很大区别.

