对一道高考调研题的教学思考

虞哲骏

(浙江省镇海中学,315200)



○解题研究○

对一道高考调研题的教学思考

虞哲骏

(浙江省镇海中学,315200)

波利亚认为“掌握数学就意味着要善于解题”.可见,解题教学是数学教育中十分重要的一环.那么，如何将数学的解题教学很好地融入到平时的课堂教学过程中呢?笔者在高三数学复习过程中,借助一道高考调研题,进行这方面的实践与探索.

题目在∆ABC中,内角A,B,C所对的边分别是a,b,c.已知acos B=bcos A,边BC上的中线长为4.

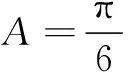
(2) 求∆ABC面积的最大值.

此题以三角函数为背景,通过三角恒等变换,考查学生有关正弦定理、余弦定理、三角形的面积公式和最值问题的求法.尤其是对于第(2)小问,综合性较强,求解方法也多种多样.同时由于不同方法的选择,也会呈现出不一样的解题过程,解法多彩多姿.由此可见,如果在开始处理题目条件时选择不当,将大大增加求解难度,而即便求解成功,也势必会耗费大量的时间.所以,在平时的教学过程中,我们要正确引导和悉心培育,逐步培养学生的思维评判能力.

下面,笔者结合上面这道题和高三复习过程中的一些体会谈谈对这方面的一些认识.

一、 一题多解

对于上面这道题的第(2)问，我们有如下几种解法.

解法1由条件，可知A=B,

c=2acos A,

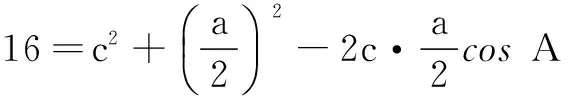
所以∆ABC的面积

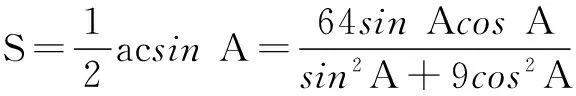
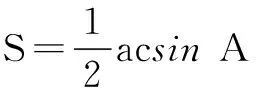
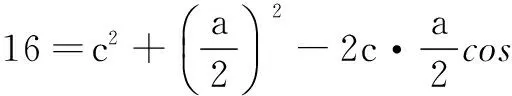
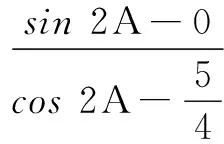
解法3根据已知条件列式，得

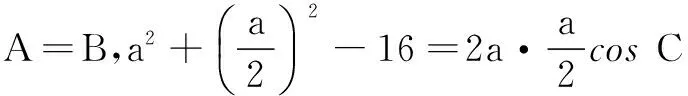
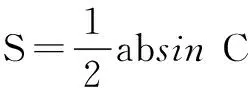
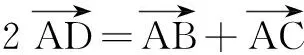
评析解法4中,平面向量的使用,使得三角形的边角关系得到一定的简化,利用三点共线和等比分点及向量数量积的几何意义相关知识,让枯燥的解三角形问题变得丰富多彩.

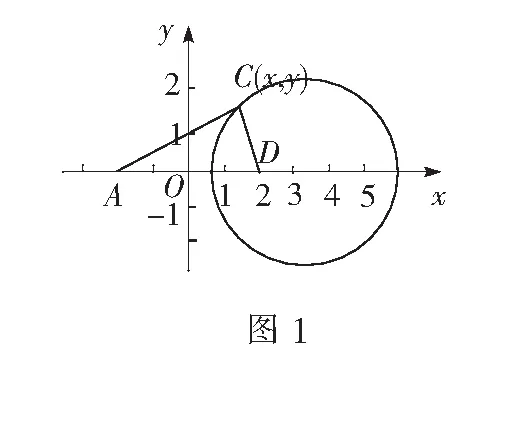
解法5如图1，以AD的中点为原点,AD所在轴为x轴建立直角坐标系,则A(-2,0),D(2,0).设C(x,y),因为CA=2CD,则

(x+2)2+y2=4(x-2)2+4y2,

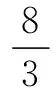
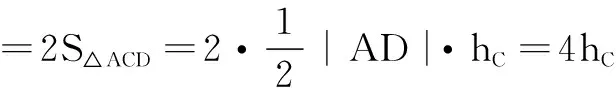
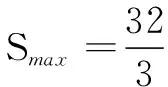
评析解法5实质上用到了解析几何中的阿波罗尼斯圆:平面中的一个动点到两个定点的距离比值是一个不等于1的常数,则该动点的轨迹是一个圆.

解决一个问题的方法有很多,在平时的数学教学中,基本要求是让学生掌握其中的一种典型解法,更高的要求是掌握一题多解,而最高的要求是让学生不仅能用多种方法解题,还会区分、评价各种解法的优劣.平时解题若能有意识地明确各种解题方法之间的联系,并在不断优化中逐步提高数学能力和数学素养,就可以消除学生学习数学的恐惧心理.当到达这个层面后,学生就能够对这类问题稍加变形,加以应用.

二、一题多变

在原题的基础上,我们可以通过改变部分条件,或者原条件和原结论互换,将问题进行变化,从而加深对这个问题的认识与理解.在平时的教学过程中,有意识地加强变式训练,可以快速有效地提高学生的应用能力,实现举一反三的目的.

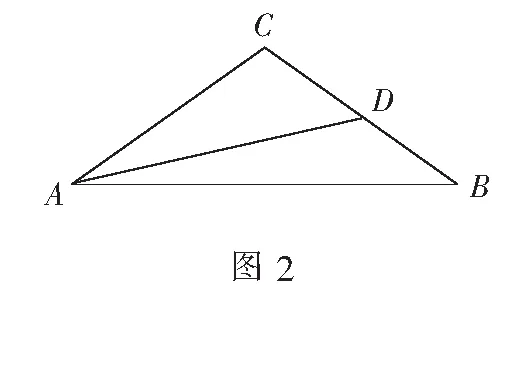
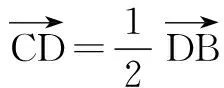
完成此题的解答与变式拓展后,学生是否已达到相应的数学辨别能力,必须建立在转化与化归思想的基础上,在实践中检验.

前苏联数学教育家奥加涅相曾说:“必须重视很多习题潜在着进一步扩展其数学功能、发展功能和教育功能的可行性.”解题是数学教学中的一个重要组成部分,也是提高学习效果不可或缺的重要环节，而一题多解是对整个解题过程活动的深层次思考,也是再发现、再创造的过程.对于高三复习阶段的学生来说,更应该培养一题多解、一题多变的能力,将所学知识灵活应用,从而将数学学好、学活、学精!

三、探根溯源

关于解三角形的中线问题,在人教A版必修5的第20页中已有涉及:∆ABC的三边分别为a、b、c,边BC、CA、AB上的中线分别记为ma、mb、mc,应用余弦定理可以证明:

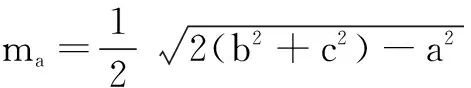
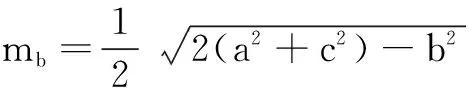
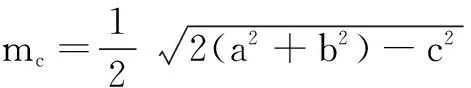
作为一名高中数学教师,对课本例题和习题要注意有针对性地进行探索和发现,并作相应的拓展.做到低起点、高要求,让学生跳出题海,深切地体会到书本就是一个巨大的宝库,从而使学生能学会知识的迁徙和创新,能够透过现象看本质.

四、题后反思

苏霍姆林斯基曾说:“必须使学生意识里有一点思维的引火线.”数学是思维的体操,在数学教学中,学生学习数学的过程就是不断思维的过程.在课堂上,数学教师只有充分地呈现、暴露学生的思维过程,才能了解学生的思维轨迹,才能不断调整教学进度与策略,呈现更精彩、更有效的课堂教学.